2018-8-30华为机试第三题

最新推荐文章于 2024-05-17 22:56:54 发布

原创最新推荐文章于 2024-05-17 22:56:54 发布 · 1.2k 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#华为机试 #递归

算法与数据结构专栏收录该内容

50 篇文章

订阅专栏

博客提及华为机试中有一个明显的递归问题，但未展开详细内容。递归是信息技术领域常用的算法思想，在机试中出现可考察相关能力。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

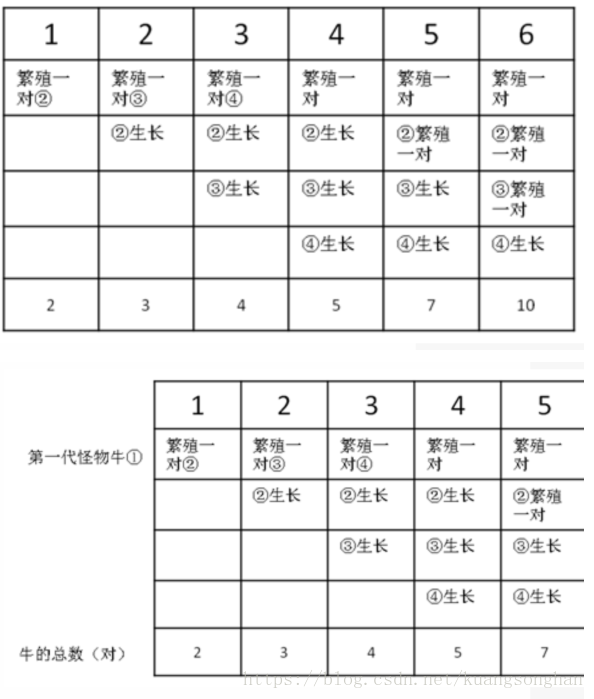
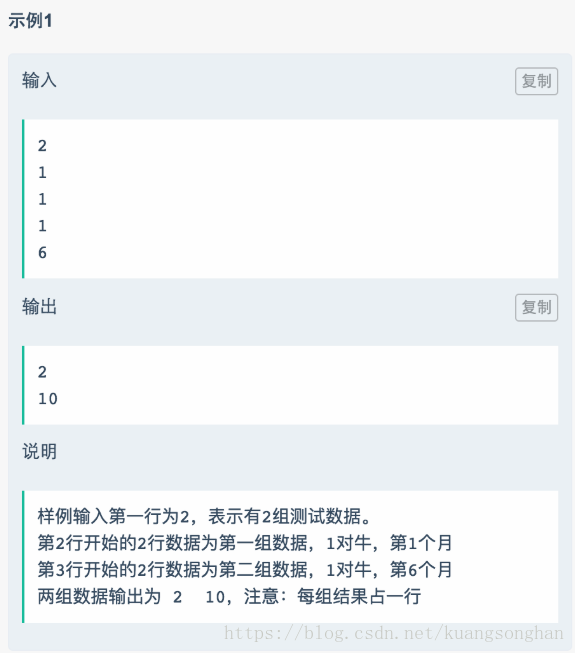
一个很明显的递归问题

package cn.csu.ksh;

import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;

public class Main2 {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		while(sc.hasNext()) {
			int n=sc.nextInt();
			int m=0;
			int k=0;
			int[][] arr = new int[n][2];
			sc.nextLine();
			for(int i=0;i<n;i++) {
				m = sc.nextInt();
				sc.nextLine();
				k = sc.nextInt();
				arr[i][0] =m;
				arr[i][1] =k;
			}
			solution(n,arr);
		}
	}
	public static void solution(int n, int[][] arr){
        List<Integer> list = new ArrayList<>();
        for(int i = 0; i<arr.length;i++){
            int beginNum = arr[i][0];
            int mouthNum = arr[i][1];
            int res = countSum(beginNum,mouthNum);
            list.add(res);
        }
        for (Integer t: list){
            System.out.println(t);
        }
    }
    public static int countSum(int beginNum, int mouthNum){
        if (mouthNum == 1){
            return beginNum+beginNum;
        }
        if (mouthNum < 5){
            return beginNum+countSum(beginNum,mouthNum-1);
        }else {
            return countSum(beginNum,mouthNum-1)+countSum(beginNum,mouthNum-4);
        }
    }
}

或者

package cn.csu.huawei;

import java.util.ArrayList;
import java.util.Scanner;

public class Main{

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		//用一个二维数组存放输入的m 和k
		int[][] arr= new int[n][2];
		for(int i=0;i<n;i++) {
			int m = sc.nextInt();
			int k = sc.nextInt();
			arr[i][0] = m;
			arr[i][1] = k;
		}
		solution(arr);
	}
	public static void solution(int[][] arr) {
		ArrayList<Integer> list = new ArrayList();
		for(int i=0;i<arr.length;i++) {
			int m = arr[i][0];
			int k = arr[i][1];
			int res = getSum(m, k);
			list.add(res);
			
		}
		for(Integer i:list) {
			System.out.println(i);
		}
	}
	
	public static int getSum(int m,int k) {
		int i=0;
		if(k<5) {
			return m*(k+1);
		}else {
			return getSum(m,k-1)+getSum(m,k-4);
		}
		
	}

}