运筹系列94：CVXPY

1. 介绍

cvx可以理解为convex的缩写。用这个包也可以用来进行混合整数规划问题建模。
简单示例如下：

import cvxpy as cp

# Create two scalar optimization variables.
x = cp.Variable()
y = cp.Variable()

# Create two constraints.
constraints = [x + y == 1,
               x - y >= 1]

# Form objective.
obj = cp.Minimize((x - y)**2)

# Form and solve problem.
prob = cp.Problem(obj, constraints)
prob.solve()  # Returns the optimal value.
print("status:", prob.status)
print("optimal value", prob.value)
print("optimal var", x.value, y.value)

2. 建模说明

variable可以是向量，可以约束为整数（integer）或者0-1变量（boolean），下面是个例子：

d = cp.Variable((n,m),integer=True) 
constraints = []
for i in range(m):
    constraints.append(cp.sum([d[j,i] for j in range(n)])<=demand.iloc[i]['需求'])
for j in range(n):
    constraints.append(cp.sum(d[j])<=cost.iloc[j]['产能']) 
objective = cp.Maximize(10*cp.sum(d) - cp.sum([cost.iloc[j]['费用']*cp.sum([d[j,i] for i in range(m)]) for j in range(n)]))
model = cp.Problem(objective, constraints)
%time model.solve(solver=cp.HIGHS)

solve的说明如下：

solve(solver=None, verbose=False, gp=False, qcp=False, requires_grad=False, enforce_dpp=False, ignore_dpp=False, **kwargs)
gp : bool, optional¶
If True, parses the problem as a disciplined geometric program instead of a disciplined convex program.

qcp : bool, optional¶
If True, parses the problem as a disciplined quasiconvex program instead of a disciplined convex program.

requires_grad : bool, optional¶
Makes it possible to compute gradients of a solution with respect to Parameters by calling problem.backward() after solving, or to compute perturbations to the variables given perturbations to Parameters by calling problem.derivative().

Gradients are only supported for DCP and DGP problems, not quasiconvex problems. When computing gradients (i.e., when this argument is True), the problem must satisfy the DPP rules.

enforce_dpp : bool, optional¶
When True, a DPPError will be thrown when trying to solve a non-DPP problem (instead of just a warning). Only relevant for problems involving Parameters. Defaults to False.

可用求解器清单如下

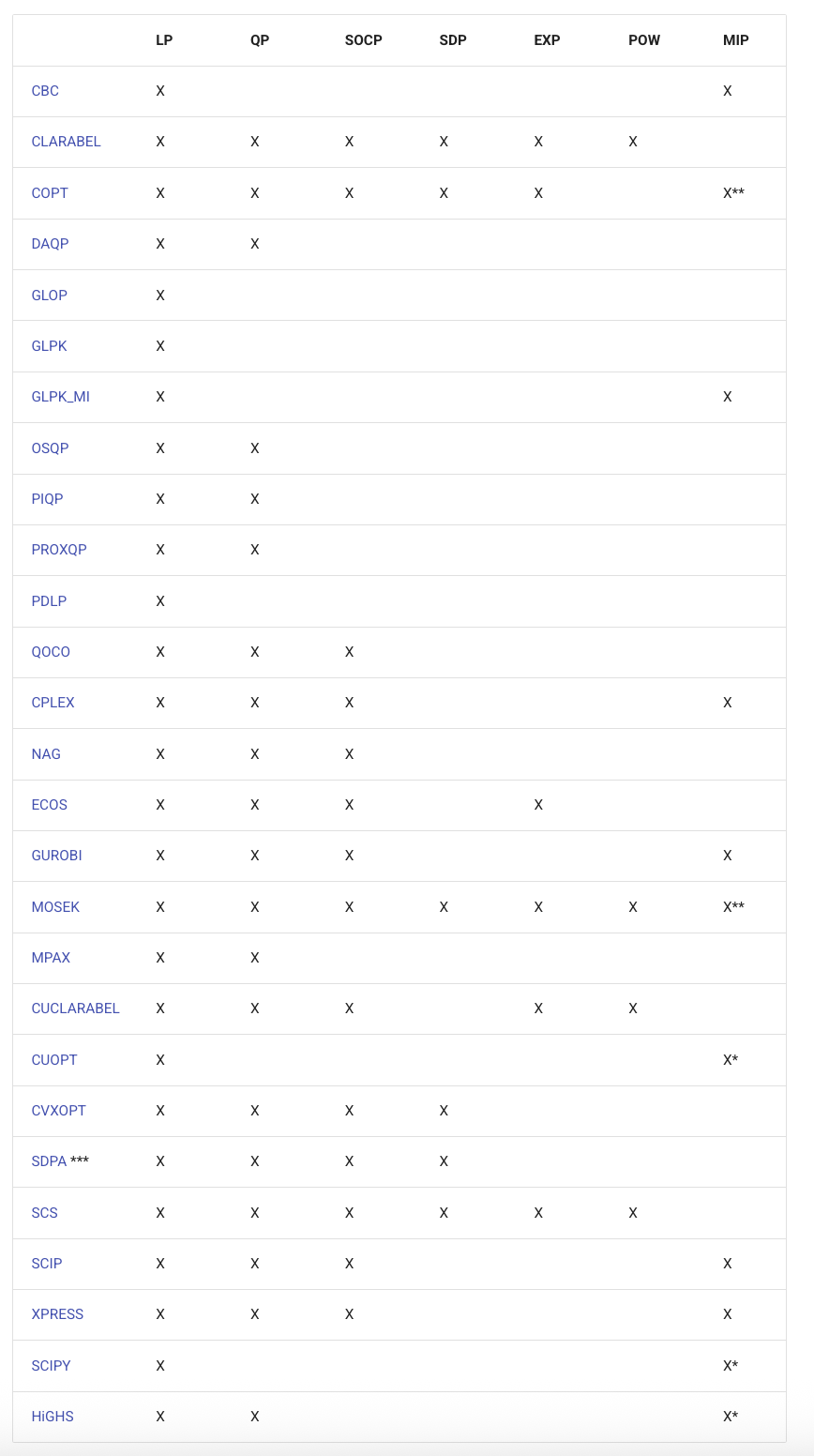
(*) Mixed-integer LP only.

(**) Except mixed-integer SDP. For COPT, mixed-integer EXP also not supported so far.

(***) Multiprecision support is available on SDPA if the appropriate SDPA package is installed. With multiprecision support, SDPA can solve your problem with much smaller epsilonDash and/or epsilonStar parameters. These parameters must be manually adjusted to achieve the desired degree of precision. Please see the solver website for details. SDPA can also solve some ill-posed problems with multiprecision support.

LP - Linear Programming refers to problems with a linear objective function and linear constraints.

QP - Quadratic Programming refers to problems with a quadratic objective function and linear constraints.

SOCP - Second-Order Cone Programming refers to problems with second-order cone constraints.

SDP - Semidefinite Programming refers to problems with semidefinite matrix constraints.

EXP - refers to problems with exponential cone constraints.

POW - refers to problems with 3-dimensional power cone constraints.

Support for power cone constraints is a recent addition (v1.1.8), and CVXPY currently does not have any atoms that take advantage of this constraint. If you want to use this type of constraint in your model, you will need to instantiate PowCone3D and/or PowConeND objects manually.

MIP - Mixed-Integer Programming refers to problems where some decision variables are constrained to be integer values.

By default CVXPY calls the solver most specialized to the problem type. For example, CLARABEL is called for SOCPs. SCS can handle all problems (except mixed-integer programs). If the problem is a QP, CVXPY will use OSQP.