机器学习笔记【二】逻辑回归与分类(1)：逻辑回归参数更新规则以及pytorch实现-优快云博客

本节为吴恩达教授机器学习笔记第二部分:逻辑回归与分类(1)-逻辑回归参数更新规则推导，包括：逻辑回归提出的背景，选用sigmoid函数的原因，极大似然方法推导参数更新规则，最后附上逻辑回归的pytorch实现以及核心的python代码。

1. 逻辑回归

忽略标签数据离散的事实用线性回归算法解决二值分类问题，效果差而且对于不在[0,1]区间的值也没有意义，为此重新构建 $h_{\theta}(x)$ 如下：
在这里插入图片描述
其中：

称为逻辑回归函数（sigmoid函数）,它定义在数据区间并且值域为(0,1)，因此 $h_{\theta}(x)$ 的值域也为(0,1)。 $g (z)$ 的导数如下：

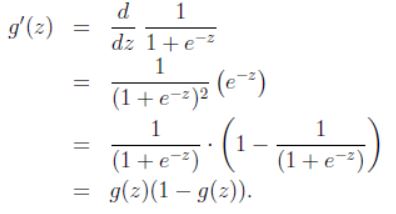
其实值域(0,1)的函数有很多，但二类问题选择sigmoid的原因也不是简单的导数形式简单啥的，是因为sigmoid函数是推到出来的。

题外：为什么逻辑回归要用sigmoid函数
https://blog.youkuaiyun.com/watermelon12138/article/details/95098070

接下来就是给定逻辑回归模型，如何确定 $\theta$ 。首先，假设：
在这里插入图片描述
即：

假设训练集中的 $m$ 个训练样本独立，我们可以得到下面的似然函数：

同样，对数似然函数更容易计算：

使用梯度下降算法， $\theta$ 更新规则如下：

因此对似然函数求导，有：
在这里插入图片描述
于是 $\theta$ 更新规则可以写为：

和最小均方算法的更新规则看起来相同，但是此处 $h_{\theta}(x)$ 已经不是 $\theta^Tx^{(i)}$ 的线性函数了。

逻辑回归，二类问题，多类应用softmax而非sigmoid。
pytorch代码

import torch
import torch.nn as nn
from torch.autograd import Variable
import numpy as np
import torch.optim as optim
import matplotlib.pyplot as plt
 
#从data.txt中读入点
with open('data.txt','r') as f:
    data_list = f.readlines()
    print(data_list)
    data_list = [i.split('\n')[0] for i in data_list]
    print(data_list)
    data_list = [i.split(',') for i in data_list]
    print(data_list)
    data = [(float(i[0]),float(i[1]),float(i[2])) for i in data_list]
    print(data)
# 标准化
x0_max = max([i[0] for i in data])
x1_max = max([i[1] for i in data])
data = [(i[0]/x0_max,i[1]/x1_max,i[2]) for i in data]
# x_data = [(float(i[0]), float(i[1])) for i in data_list]
# y_data = [(float(i[2])) for i in data_list]
 
X0 = list(filter(lambda x: x[-1] == 0.0, data))#选择第一类的点
X1 = list(filter(lambda x: x[-1] == 1.0, data))#选择第二类的点
plot_X0_0 = [i[0] for i in X0]
plot_X0_1 = [i[1] for i in X0]
plot_X1_0 = [i[0] for i in X1]
plot_X1_1 = [i[1] for i in X1]
plt.plot(plot_X0_0,plot_X0_1,'ro',label='x_0')
plt.plot(plot_X1_0,plot_X1_1,'bo',label='x_1')
plt.legend(loc='best')
plt.show()
 
#将数据转换成numpy类型，接着转换成Tensor类型
np_data = np.array(data,dtype='float32')#转成numpy array
x_data = torch.from_numpy(np_data[:,0:2])#转换成Tensor,大小是[100,2]
y_data = torch.from_numpy(np_data[:,-1]).unsqueeze(1)#转成tensor，大小是[100,1]
 
class LogisticRegression(nn.Module):
    def __init__(self):
        super(LogisticRegression,self).__init__()
        self.lr = nn.Linear(2,1)
        self.sm = nn.Sigmoid()
 
    def forward(self, x):
        x = self.lr(x)
        x = self.sm(x)
        return x
 
logistic_model = LogisticRegression()
if torch.cuda.is_available():
    logistic_model.cuda()
else:
    logistic_model = LogisticRegression()
 
criterion = nn.BCELoss()
optimizer = optim.SGD(logistic_model.parameters(),lr=1e-3,momentum=0.9)
 
for epoch in range(50000):
    if torch.cuda.is_available():
        x = Variable(x_data).cuda()
        y = Variable(y_data).cuda()
    else:
        x = Variable(x_data)
        y = Variable(y_data)
 
    #向前传播
    out = logistic_model(x_data)
    loss = criterion(out,y_data)
    print_loss = loss.item()
    #向后传播
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()
    #计算正确率
    mask = out.ge(0.5).float()
    acc = (mask == y_data).sum().item()/y_data.shape[0]
 
    if(epoch+1)%1000 == 0:
        print('*'*10)
        print('epoch{}'.format(epoch+1))
        print('loss is {:.4f}'.format(print_loss))
        print('acc is {:.4f}'.format(acc))
 
w0,w1 = logistic_model.lr.weight[0]
w0 = w0.item()
w1 = w1.item()
b = logistic_model.lr.bias.item()
plot_x = np.arange(30,100,0.1)
plot_y = (-w0*plot_x-b)/w1
plt.plot(plot_x,plot_y)
plt.show()

python核心代码

    # Logistic函数
    def logistic(self,wx):
        return 1.0 / (1.0 + exp(-wx))
        
    def train(self,dataMat, target,weights):
        for k in range(self.steps):
            # wx
            gradient = dataMat * mat(weights)
            # sigmoid(wx)
            output = self.logistic(gradient)  # logistic function
            errors = target - output  # 计算误差
            weights = weights + self.alpha * dataMat.T * errors
        return weights