TGM-COT：高效节能的连续目标跟踪

TGM‐COT：基于双层网格模型的无线传感器网络中高效节能的目标跟踪方案

1 引言

微传感器加工技术和无线通信技术的快速发展推动了微型化、高度集成且多功能节点的发展。这些节点成本低廉，可大规模部署，能够形成一个自组织网络，在感兴趣区域自发地感知、收集和处理数据[1–3]。如今，无线传感器网络（WSNs）已广泛应用于各种场景，从生境监测到军事监视[4]。无线传感器网络提供的最重要服务之一是目标跟踪。传统上，目标跟踪的实现包括两个阶段，即监测与报告。监测阶段旨在识别围绕目标边界的节点。当目标侵入监测区域时，一部分节点可通过传感模块检测到该目标。通过信息交换，可以确定位于边界附近的节点，以描述目标的运动轨迹。报告阶段旨在选择报告节点，并及时将边界节点的信息传输至汇聚节点[5–7]。

通常，需要监测和跟踪的目标可分为两类：连续对象和个体对象。个体对象可能是敌方士兵、坦克或单个野生动物，具有固定尺寸并占据有限区域。与个体对象不同，连续对象（如有毒气体、野火和迁徙的羊群）在大范围区域内连续分布。由于对周围自然环境的敏感性，连续对象具有灵活且动态的特性。尽管已有大量关于个体对象跟踪研究[8–15], ，但这些方法无法直接应用于连续对象跟踪。由于连续目标通常覆盖面积大且形状和大小不固定，实时跟踪此类目标需要大量交换的消息，这一过程会产生巨大的通信开销。此外，在不考虑能量补充的情况下，无线传感器网络面临的最大挑战是能量受限，因此必须提出一种高效的跟踪算法，以尽可能最小化通信开销。

本文提出了一种名为TGM‐COT的节能算法，用于连续目标跟踪。为TGM‐COT专门设计了一种基于两层网格的网络模型。在TGM‐COT中，首先在感知区域上主动建立粗粒度网格，然后在靠近连续对象的粗粒度网格单元内建立细粒度网格。基于该两层网格结构建立了一个基于簇的网络。通过将大量计算任务分配给簇头，减少了非簇头节点的通信量。此外，考虑到节点分布不均的问题，该算法引入了一种精简机制，以消除高节点密度区域中的冗余节点，同时引入一种避让机制，防止在低节点密度区域出现边界失真。

TGM‐COT的主要贡献在于：
(a) 在TGM‐COT中，数据流为单向，数据传输量可减少一半。
(b) 由于采用两层基于网格的模型，簇头可在不降低跟踪精度的情况下移除冗余的边界节点。
(c) 提出了一种避让机制，以解决因节点分布不均导致的边界失真问题。

本文的其余部分组织如下：在第2节中，我们讨论了先前的工作并进行了分析。在第3节中，我们给出了预备知识，并介绍了基于双层网格的网络模型。第4节介绍了双层网格网络的划分。边界节点识别机制和精简机制在第5节中描述。在第6节中，通过仿真评估了TGM‐COT的性能。最后，我们得出结论。

2 相关工作

在本节中，我们简要回顾了一些突出的连续对象跟踪算法。

在[16], Chang等人提出了一种连续目标检测与跟踪算法（CODA）。CODA基于一种混合静态/动态聚类技术，使每个节点能够检测和跟踪移动的感知区域中目标的边界。为了估计每个簇内的边界轮廓，CODA在静态簇中使用簇头。每个动态簇头融合其所在簇内的所有边界信息，然后以压缩数据格式将信息传送给汇聚节点。无论连续对象的大小和传感器网络密度如何，CODA都具有较低的通信开销并实现更优的边界估计精度。然而，如果边界轮廓为凹多边形，则可能从原始扩散的目标中获取错误的边界信息。

在[17], Kim等人提出了一种名为DEMOCO的节能算法，用于连续移动现象的边界检测与监控。该方法通过从边界节点中选择代表节点上传数据，减轻了边界节点与汇聚节点之间的流量负载。此外，一个代表节点仅发送一个邻居节点的ID，该邻居可能是其具有不同当前读数的邻居中距离最近的一个。这意味着报告消息大小可以更小，尤其是在部署节点密度较高的情况下。然而，在边界节点识别过程中，DEMOCO引入了相邻节点之间大量的消息交换。此外，当目标边界缩小时，DEMOCO将位于目标所占区域内的节点选为边界节点。这在某些实际场景中是不合理的。图1说明了对有毒气体的跟踪情况。U1由节点1、2、…和7组成（图1a），是内边界节点集合。U2由节点A、B、…和N组成（图1b），是外边界节点集合。显然，在U1和U2之间存在一个空白区域，其中含有有毒气体。DEMOCO确定的内边界节点忽略了该空白区域的存在，可能导致一线人员被误导进入污染区域。

在[18], Parket等人提出了一种考虑基于网格结构的新型连续目标跟踪方案。为了满足灵活性的要求，该方案首先构建一个粗粒度网格结构。一旦出现连续对象，便在周围粗粒度网格单元内建立细粒度网格。考虑到可靠性，细粒度网格结构中的微小网格单元能够提供连续对象边界的详细形状。为了快速应对连续对象的扩散，该方案在连续对象扩散方向上的下一个粗粒度网格单元内执行细粒度网格划分。然而，该方案未考虑节点分布不均的问题。因此，如果某个网格中没有节点，即使目标穿过该网格，该网格也无法被选为边界网格。基于网格的模型也在[19–21],的研究中被采用，在本研究中，我们对该模型进行了改进，并设计了双层网格模型。

3 网络模型

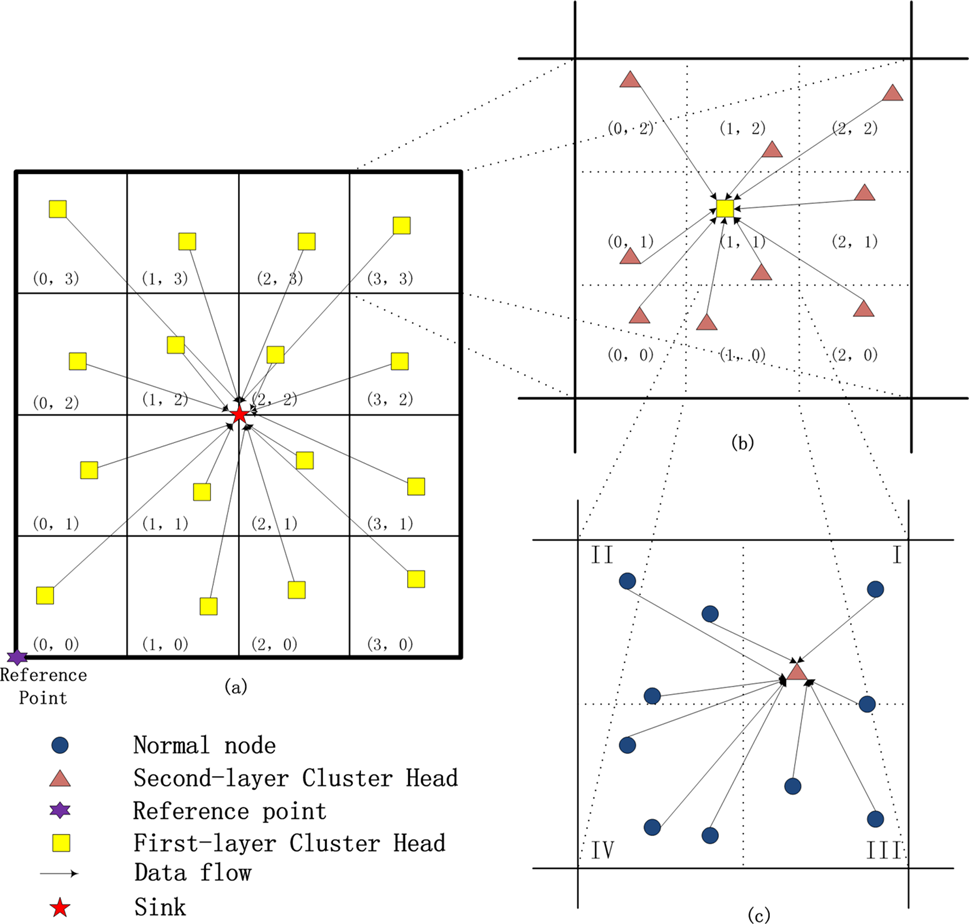
在本节中，我们对传感器节点和传感器网络架构做出一般性假设。如图2a所示，感知区域被定义为一个方形区域，可划分为多个网格划分。这些网格划分代表第一层网格。一个预定义的系统参数a决定网格划分的大小（a在图2a中为4）。如图2b所示，在第一层网格内构建第二层划分。一个预定义的系统参数b（b在图2b中为3）决定网格的大小。参数a和b的值在网络初始化阶段设定。每个第二层网格内的四分划分如图2c所示。此外，我们假设该传感器网络具有以下特性。

1. 节点在感知区域中随机部署。
2. 每个节点以及汇聚节点均为准静止状态。
3. 每个传感器可自动调整其感知范围[22]。
4. 每个节点通过全球定位系统[23]或其他定位技术[24]具备位置感知能力。
5. 不考虑可能的数据丢失或拥塞情况。
6. 每个节点均可实现时间同步。

4 双层网格结构

4.1 第一层网格构建

在图2a中，一个六角星位于坐标点ðx0; y0Þ处。该六角星表示一个参考点。基于该参考点，可以构建第一层网格，并获得其对应的坐标，记为Cfirst gridða; bÞ。每个节点都可以通过以下公式计算其所属网格的坐标：
a ＝ x x0ð Þ= Xm=að Þ b c; b ＝ y y0ð Þ= Ym=að Þ b c；其中(x, y)为传感器节点坐标。Xm和Ym分别为监测区域的长度和宽度。为简化且不失一般性，我们假设Cfirst gridða; bÞ的坐标为正整数。

在同一个网格中部署的传感器节点形成一个簇。在该簇中，剩余能量较大且更靠近第一层网格中心的节点更有可能被选为第一层簇头。该簇头充当第二层簇头与汇聚节点之间的中介。为了竞争成为簇头，每个节点都被分配一个退避时间Tbackoff big，该时间通过公式（1）计算得出。

$$
T_{\text{backoff big}} = \frac{R}{E_{\text{residual 1}}} \quad (1)
$$

其中Eresidual 1表示剩余能量，R表示传感器节点与第一层网格中心之间的距离。关于R的数学表达式见公式 (2)：

$$
R = \left{
\begin{array}{c}
\left( x - x_{X_m / a} + \frac{1}{2} \cdot \frac{X_m}{a} \right)^2 + \
\left( y - y_{Y_m / a} + \frac{1}{2} \cdot \frac{Y_m}{a} \right)^2
\end{array}
\right}^{1/2} \quad (2)
$$

在Tbackoff big过期后，该节点将在其所属的第一层网格内广播一个广告包，并宣布自己成为第一层簇头。如果某个节点收到来自其他节点的广告包，它将提取该包中第一层簇头的位置信息。

4.2 第二层网格形成

如图2b所示，第二层网格基于第一层网格构建。一个节点可以计算其所属的第二层网格的坐标，记为Csecond gridðc;dÞ，如下所示：

$$
c = \left\lfloor \frac{x - a \cdot X_m / a}{X_m / (a b)} \right\rfloor \quad (3)
$$

$$
d = \left\lfloor \frac{y - b \cdot Y_m / a}{Y_m / (a b)} \right\rfloor \quad (4)
$$

其中a和b是节点所属的第一层网格的坐标参数。

同一第二层网格内的所有节点构成一个簇。在该簇中，选择一个第二层簇头作为非簇节点与第一层簇头之间的中介。由于第二层网格的规模较小，因此在簇头选举中仅将剩余能量作为衡量指标。类似地，我们为每个节点定义一个退避时间，以竞争成为簇头。

$$
T_{\text{backoff small}} = \frac{1}{E_{\text{residual}}} \quad (5)
$$

退避时间结束后，每个节点通过广播包含其ID、第一层网格和第二层网格坐标的广告包，试图赢得簇头选举。如果一个节点在相同的第一层和第二层网格内收到来自其他节点的广告包，它将撤回自己的广告，并从接收到的包中提取第二层簇头的位置信息。

为了节约能量，每个节点能够在不同的传输功率下工作。普通节点和第二层簇头的通信半径分别表示为Rtrans node和Rtrans level 2。为了保持普通节点与第二层簇头之间的连通性，以及第一层簇头与第二层簇头之间的连通性，a；b和通信半径R之间的关系应满足公式(6)和(7)给出的约束条件：

$$
R_{\text{trans level 2}} \geq \sqrt{ \left( \frac{X_m}{a} \right)^2 + \left( \frac{Y_m}{a} \right)^2 } \quad (6)
$$

$$
R_{\text{trans node}} \geq \sqrt{ \left( \frac{X_m}{a b} \right)^2 + \left( \frac{Y_m}{a b} \right)^2 } \quad (7)
$$

通过求解公式(6)和(7)，可得到a；b的值：

$$
a \geq \frac{ \sqrt{ (X_m)^2 + (Y_m)^2 } }{ R_{\text{trans level 2}} } \quad (8)
$$

$$
b \geq \frac{ \sqrt{ (X_m)^2 + (Y_m)^2 } }{ a \cdot R_{\text{trans node}} } \quad (9)
$$

4.3 四分划分设计

为了避免因节点分布不均导致的目标边界失真，我们提出了一种四分划分方法。该方法使TGM‐COT在有毒气体监测方面更具实用性。如图2c所示，四分划分构建于第二层网格内。每个第二层网格被划分为四个子区域，即区域I、区域II、区域III和区域IV。

5 连续目标跟踪与边界检测

5.1 定义

定义1（节点值—VON）
节点的默认值设为0。如果一个节点能够检测到事件，则该节点的值（节点值—VON）更改为1。

定义2（值变化的节点—NCV）
与之前时刻（即在时隙 $ t - 1 $）相比，在当前阶段（即在时隙 $ t $）具有不同值的节点被定义为NCV。

定义3（候选边界节点—CBNs）
候选边界节点是位于目标边界周围的一个节点。在CBN的通信范围内至少存在一个具有不同值的节点。

定义4 (Vratio)
Vratio是相应四分划分网格中节点总数里值为1的节点所占的百分比。

5.2 提出的算法

TGM‐COT 包含一种针对候选边界节点设计的精简机制和一种数据上传机制。

步骤1 节点U周期性激活以执行局部检测。
步骤2 当节点U成为NCV时，它将向其第二层簇头发送一条通知消息（NM）。第二层簇头更新非簇节点的信息以统计NCV的数量。
步骤3 边界节点识别

根据Vratio，四分划分区域中边界节点的识别可分为三种情况。

情况1 $ 0 < \text{Vratio} < 1 $
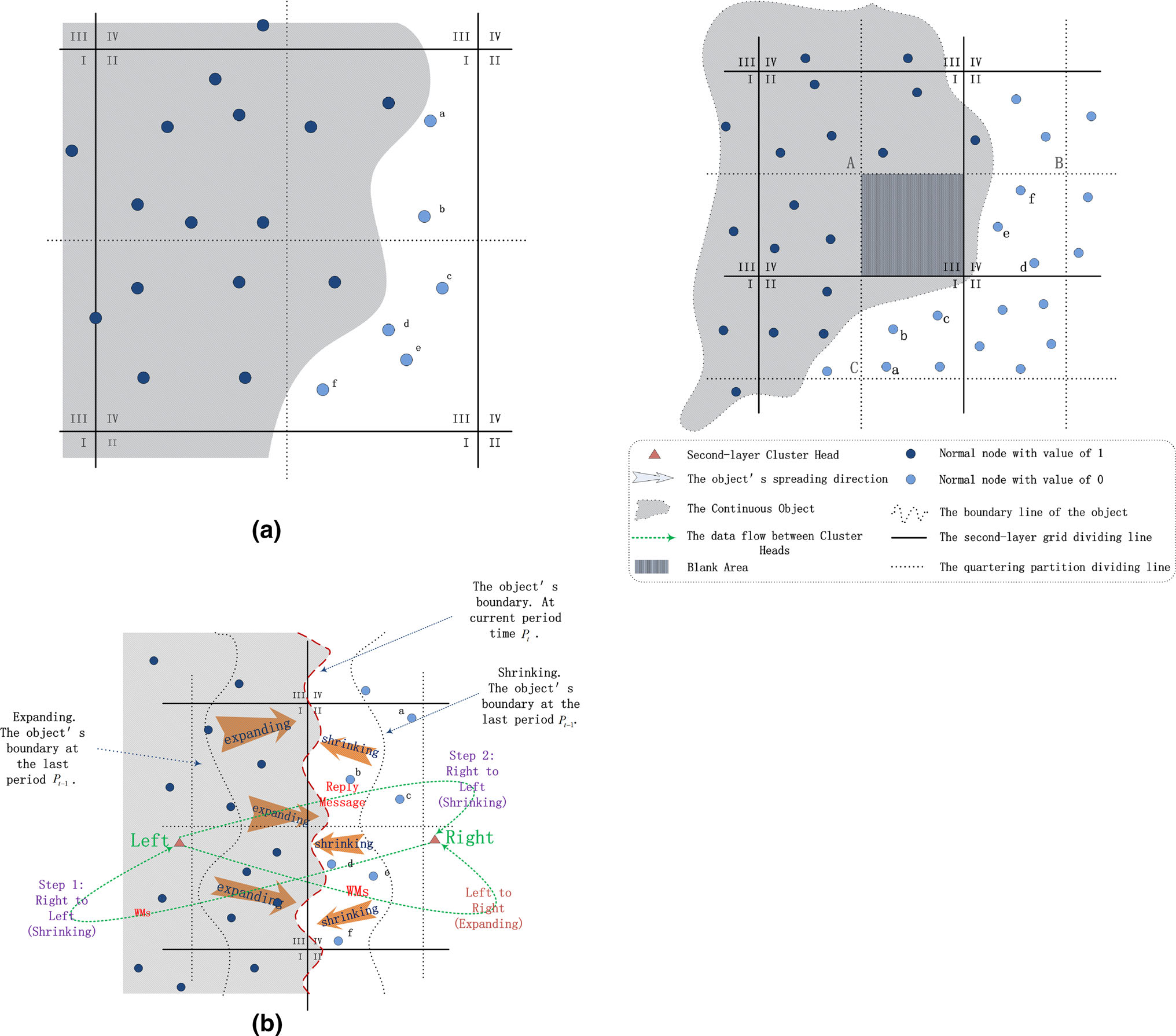
在这种情况下，值为0和1的节点同时存在于四分划分中。选择值为0的节点作为CBNs。如图3a所示，节点a–f为CBNs。

情况2 $ \text{Vratio} = 1 $ 或 $ \text{Vratio} = 0 $
在这种情况下，所有节点的值均为1，或所有节点的值均为0，位于相应的四分划分中。当目标边界扩展时，一部分节点的值变为1。相反，当目标边界收缩时，节点的值变为0。图3b展示了一个示例情况。在图3b中，一个连续对象从左向右移动。在左簇中，所有节点都能检测到目标，因此被赋值为1。在右簇中，没有任何节点能检测到该目标，因此被赋值为0。由于四分划分中的节点无法满足 $ 0 < \text{Vratio} < 1 $ 的情况，因此无法使用情况1中的识别规则来识别边界节点。在这种情况下，出现了边界失真现象。为了避免边界失真现象，每个第二层簇头会向其相邻的第二层簇头发送一条警告消息（WM），其中包含发送方的第一层坐标、第二层坐标以及相应的四分划分编号。如图3b所示，当目标扩展时，那些在 $ P_{t-1} $ 时刻无法检测到目标但在当前时刻 $ P_t $ 能够检测到目标的节点将向其第二层簇头发送通知消息，簇头可通过统计分析计算Vratio。通知消息从左四分区传输到右四分区，右侧的第二层簇头根据统计分析结果进行判断。如果 $ \text{Vratio} = 0 $，左簇的簇头将向右簇的簇头发送回复消息，通知其簇内所有节点的值均为0，从而确保所识别的所有CBNs均为外侧型。随后，右簇的簇头可在其相关的四分划分区域内识别相应的CBNs。根据上述提出的边界识别机制规则可知，无论目标扩展还是收缩，节点a–f始终为外侧型 CBNs。

情况3 一种特殊情况
在图3c中，深色条纹区域是没有任何节点的空白区域。第二层簇头A在初始阶段将该区域标记为空白区域。如果目标进入该区域，第二层簇头A将向其相邻的第二层簇头B和C发送唤醒消息。一旦相邻的第二层簇头B和C接收到唤醒消息，它们将进行本地判断，确定属于哪种情况（情况1或情况2）。根据上述分析，节点a–f在其相应区域中被识别为CBNs。因此，该预防机制能有效避免边界失真现象。

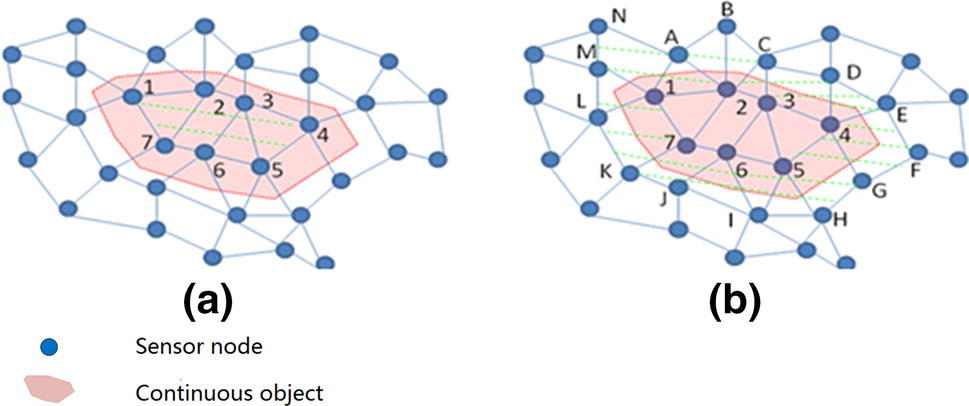
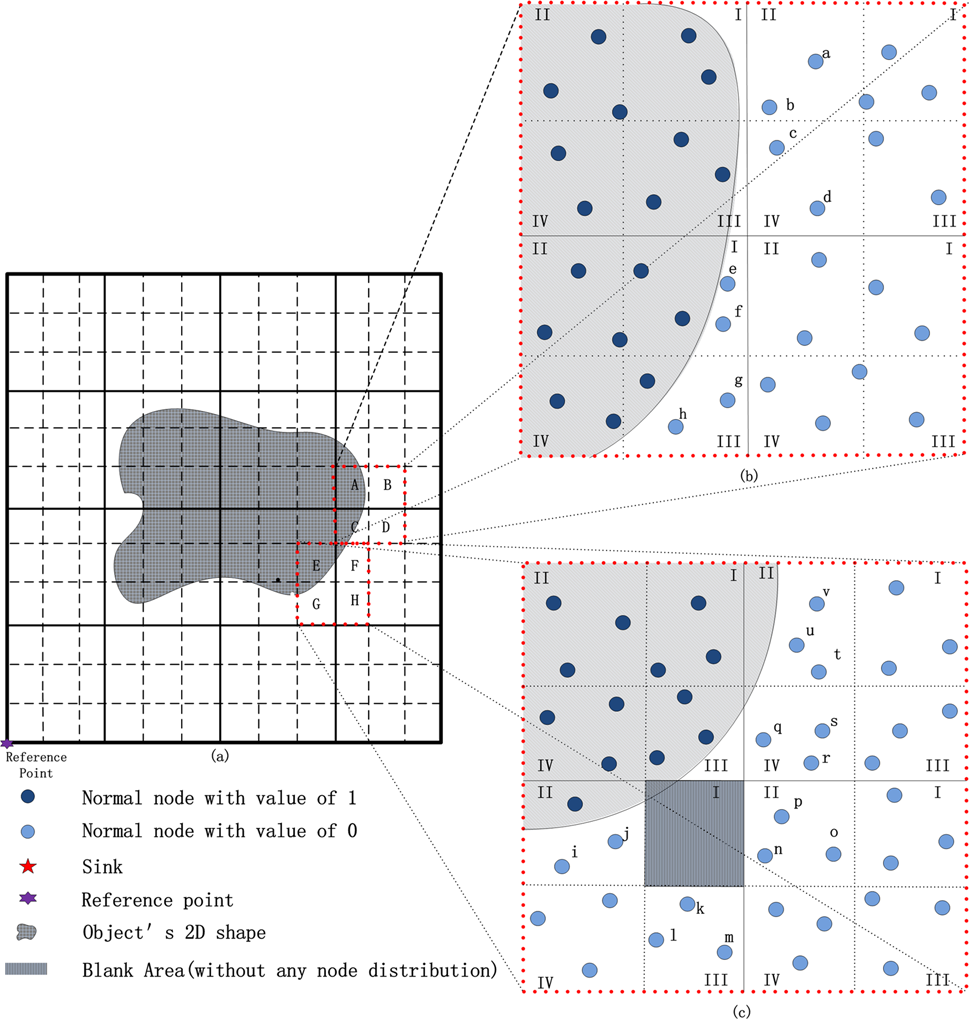
图4说明了上述边界节点识别的三种情况。在图4a中，区域C的场景是情况1的一个示例。根据判断准则：$ 0 < \text{Vratio} < 1 $，节点e–h可被识别为CBNs。类似地，区域G中的节点i和j也是CBNs。根据情况2的判断准则，区域B中的节点a–d被识别为CBNs。区域F中的节点q–v也是如此。区域G中存在一个空白区域。当目标进入区域G时，区域E中的一个簇头将向其在区域G和F中的相邻簇头发送唤醒消息。然后，区域G和F中的第二层簇头运行局部边界节点识别机制，节点k–p被识别为CBNs。

步骤4 简化机制
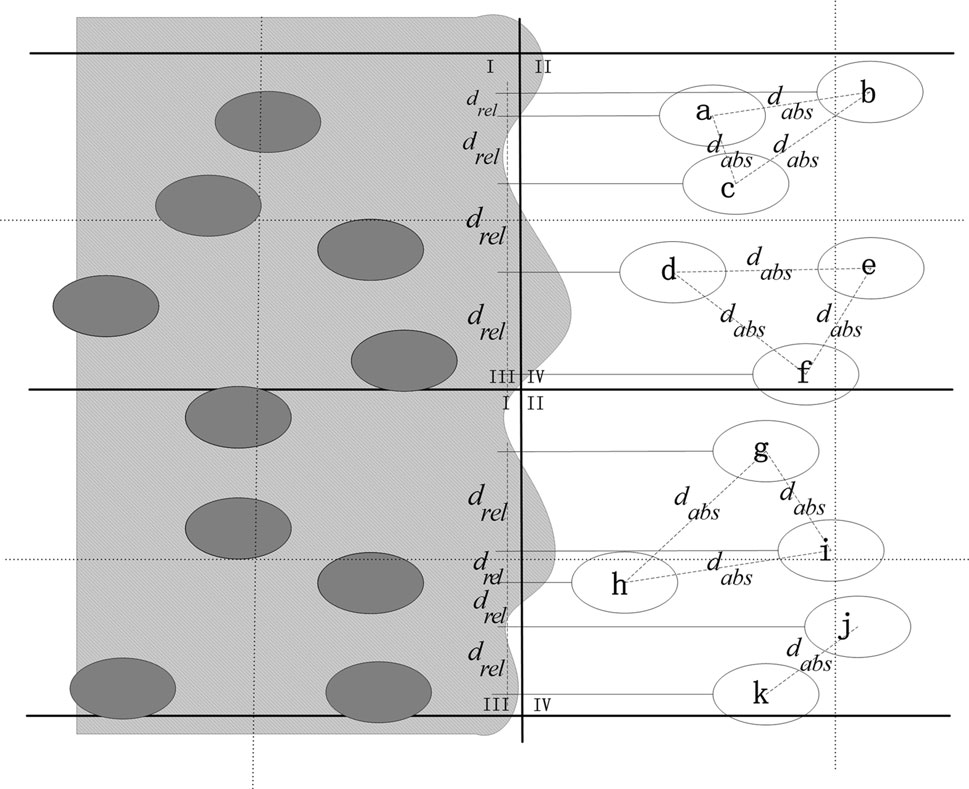
根据上述分析，可以有效地识别CBNs。然而，由于节点通常密集部署，许多冗余节点可能被识别为CBNs。为了解决这个问题，我们引入了两种距离概念：相对距离 $ d_{\text{rel}} $ 和绝对距离 $ d_{\text{abs}} $。$ d_{\text{abs}} $ 是欧几里得距离。$ d_{\text{rel}} $ 是两个CBN在网格线上的投影距离。只有当 $ d_{\text{abs}} > r $ 且 $ d_{\text{rel}} > e $（$ e $ 和 $ r $ 为系统参数）时，该节点才能被视为最终边界节点。

在图5中，CBNs为a；b；…；j和k。尽管节点h和i之间的 $ d_{\text{abs}} $ 满足约束条件：$ d_{\text{abs}} > r $，但相对距离 $ d_{\text{rel}} $ 无法满足要求：$ d_{\text{rel}} > e $。最终，节点a–k被选为最终边界节点。

步骤5 数据上传
让所有边界节点都参与数据上传是不明智的。由于普通节点的信息存储在第二层簇头中，第二层簇头只需提取并压缩这些信息，然后发送给相应的第一层簇头。每个第一层簇头将从第二层簇头接收信息并将它们转发到汇聚节点。图2a、b 显示了数据流的方向。单向数据从普通节点上传到第二层簇头，然后从第二层簇头传送到第一层簇头，最后从第一层簇头传送到汇聚节点。

6 性能评估

在本节中，通过使用Matlab进行的一系列仿真评估了TGM‐COT的性能。TGM‐COT与连续对象跟踪算法DEMOCO和TG‐COD进行了比较。

6.1 仿真设置

在仿真中，节点被随机部署在一个100米 × 100米的正方形区域内。连续对象的形状被模拟为一个四分之一圆。该目标从网络的左下角开始，初始半径为0米，并以每秒一米的速度扩散。跟踪周期设置为1个时隙，实验结果每第20个时隙记录一次。活跃模式和睡眠模式的功耗率分别为3毫瓦和15微瓦。发送和接收功耗率分别为35和38毫瓦[25]。我们对200次仿真运行的结果取平均值，以减少偶然误差。节点ID、第一层网格坐标和第二层网格坐标均假设为1字节。a和b的值分别为3和4。

我们将TGM‐COT与DEMOCO[17]和TG‐COD[18]在边界节点与代表性节点数量、交换的数据包数量、能耗以及跟踪精度方面进行比较。我们分析了通信范围R和节点数量N对跟踪算法性能的影响。

1. 边界节点和代表节点数量
   冗余边界节点和报告节点会带来更多的消息交换。在确保跟踪精度的前提下，应尽量减少参与目标跟踪的节点数量。

2. 交换的数据包数量
   交换的数据包分为两类：控制消息和报告消息。前者在边界识别过程中交换，后者则传输至汇聚节点。

3. 能耗
   我们分别记录从开始到当前时间段所消耗的能量，以及每个时隙的能耗。

4. 跟踪精度
   我们定义一个参数 $ e(i) $ 在公式(10)中用以量化跟踪精度：

$$
e(i) = \frac{ \sum_{j=1}^{m} \sqrt{ (r(j) - r)^2 } }{m} \quad (10)
$$

其中，$ r(j) = \sqrt{x_j^2 + y_j^2} $；m 表示边界节点数量；$ \sqrt{(r(j) - r)^2} $ 表示坐标为 $ (x_j, y_j) $ 的边界节点与目标真实边界之间的绝对距离。$ e(i) $ 的值越接近0，表示该算法能达到的跟踪精度越高。

6.2 仿真结果

6.2.1 跟踪轮廓快照

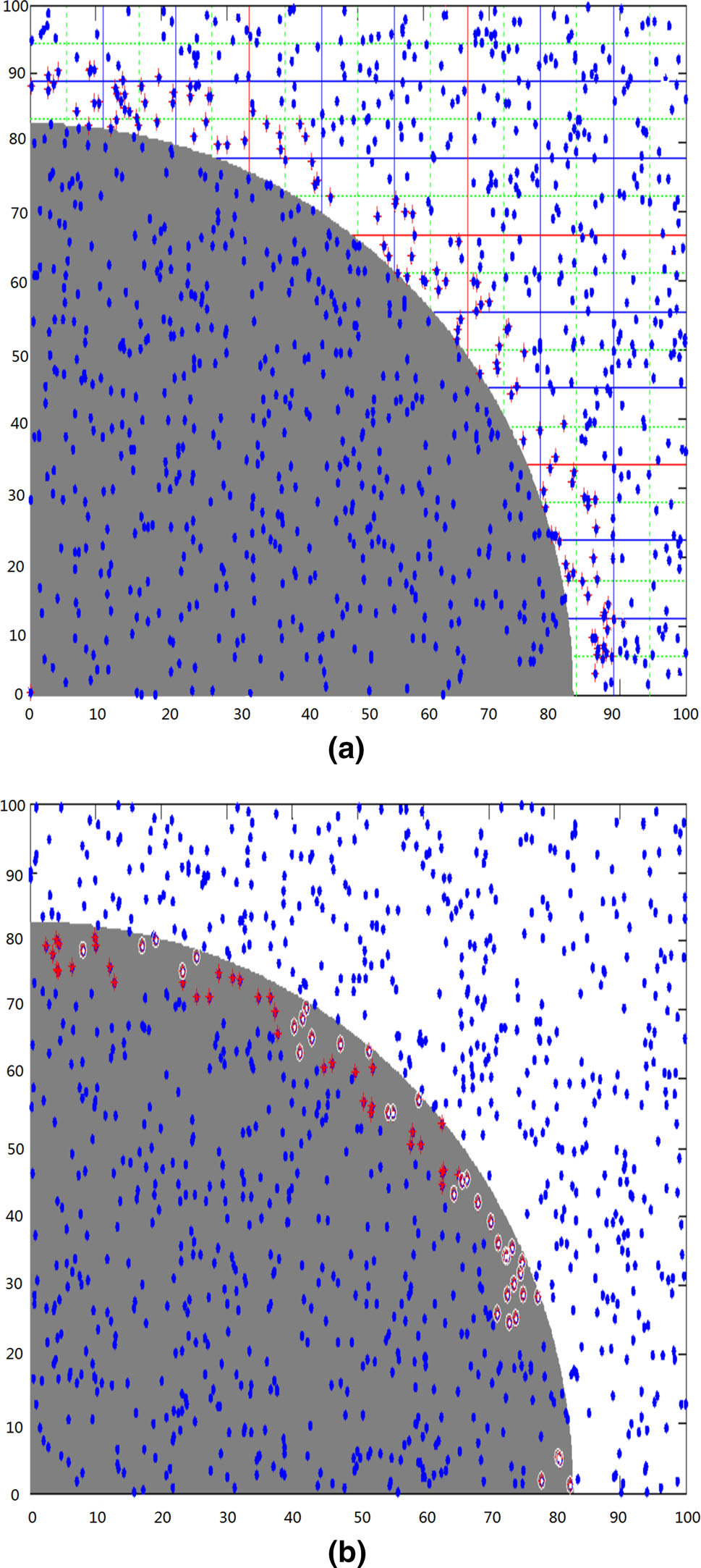
图6展示了在第200个时隙时一个收缩目标的跟踪快照。蓝色节点表示普通节点，红色节点表示当前的边界节点。对比显示，在图6a中，边界节点始终分布在目标的外部边界上；而在图6b中，边界节点全部位于目标的内部边界上。可以理解的是，在DEMOCO中，当目标收缩时，发送CompareOneZero消息（COZ）的变化值节点（CVNs）位于目标外部，因此那些邻近CVN但位于目标内部的节点即为边界节点。相反，当目标扩张时，边界节点则位于目标边界之外。然而，TGM‐COT对目标的扩张或收缩具有较强的鲁棒性。在图6b的右下角存在边界失真现象，这是因为DEMOCO没有采取任何预防措施来应对节点分布不均的问题。基于上述分析，我们可以得出结论：与DEMOCO相比，TGM‐COT在跟踪连续对象方面更加实用且适用。

6.2.2 边界节点和报告节点数量

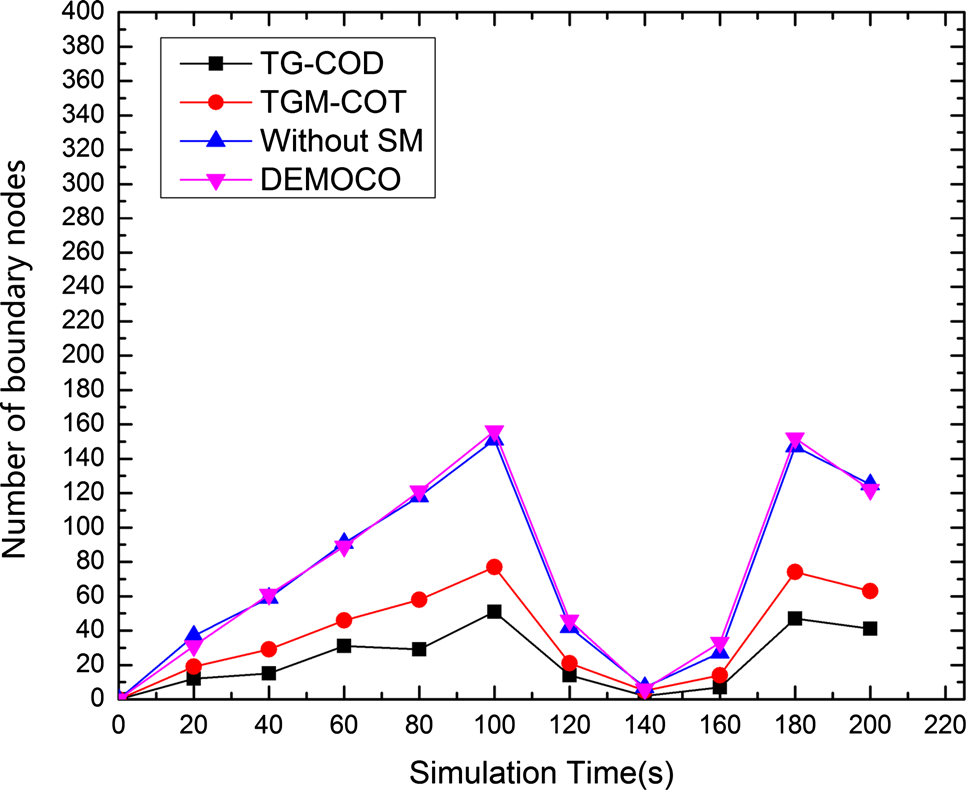
边界节点和报告节点的数量反映了算法的跟踪效率。在确保跟踪精度的前提下，更少的边界节点和报告节点有助于提高能量效率。图7显示了三种算法所识别的边界节点数量。三条曲线具有相同的趋势，该趋势由目标的扩散决定。扩散规则遵循一个循环过程。随着目标的移动，目标覆盖的区域逐渐扩展并达到最大值，随后目标开始收缩。需要指出的是，在任何时候，DEMOCO生成的边界节点数量均多于TGM‐COT。这是因为在DEMOCO中无法消除对跟踪精度无益的冗余节点。

TGM‐COT产生的边界节点比TG‐COD更多，这是由于两者采用的识别机制不同。TG‐COD使用网格作为边界节点以实现节能，但通过网格描述目标边界会降低跟踪精度。

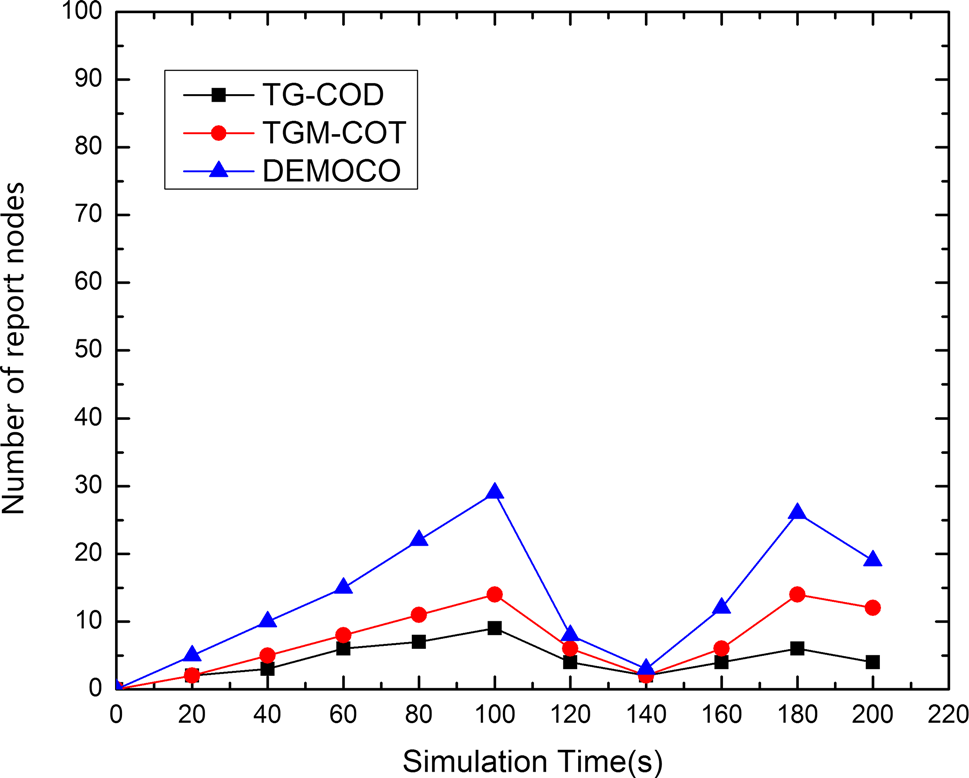
在图8中，我们比较了各算法生成的报告节点数量。三条曲线具有相同的变化趋势，由目标扩散决定。DEMOCO中的报告节点是指在其通信范围内能够覆盖邻近边界节点的节点，报告节点数量与通信半径R相关。而TGM‐COT中的报告节点仅为第一层簇头，因此DEMOCO的报告节点数量大于TGM‐COT。然而需要指出的是，TGM‐COT生成的报告节点略多于TG‐COD，因为TG‐COD通过使用一定比例的边界节点来实现目标扩张与收缩之间的动态平衡过程。

6.2.3 交换消息数量

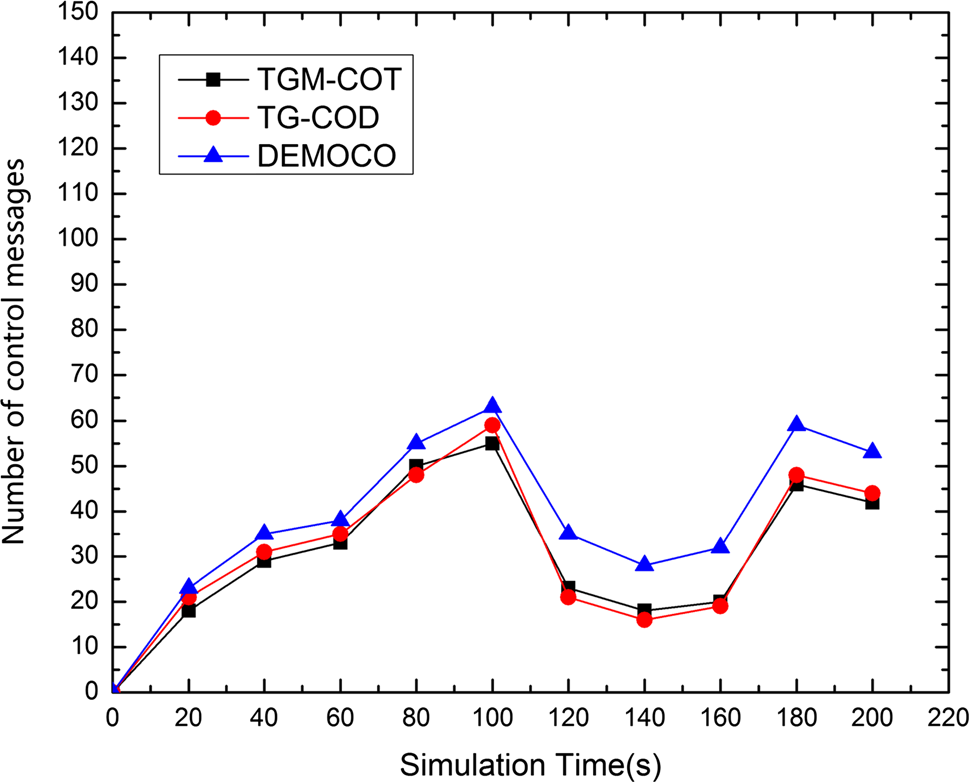
在本节中，我们比较目标跟踪过程中产生的通信开销。流量负载是由控制消息和报告消息共同构成的。前者表示在边界节点识别过程中生成的消息，后者表示由报告节点发送给汇聚节点的消息。较少的消息交换体现了能量效率和及时性的特点。

图9比较了TGM‐COT、TG‐COD和DEMOCO随时间广播的控制消息的变化情况。控制消息数量随着目标半径的增大而增加，随后随着目标半径的减小而下降。

在DEMOCO中，边界节点由CVN节点发送的COZ消息确定。然而，在TGM‐COT和TG‐COD中，作为报告节点的第一层簇头是在网络初始化阶段选定的。这意味着在TGM‐COT和TG‐COD中，用于选择报告节点的控制消息可以省略。

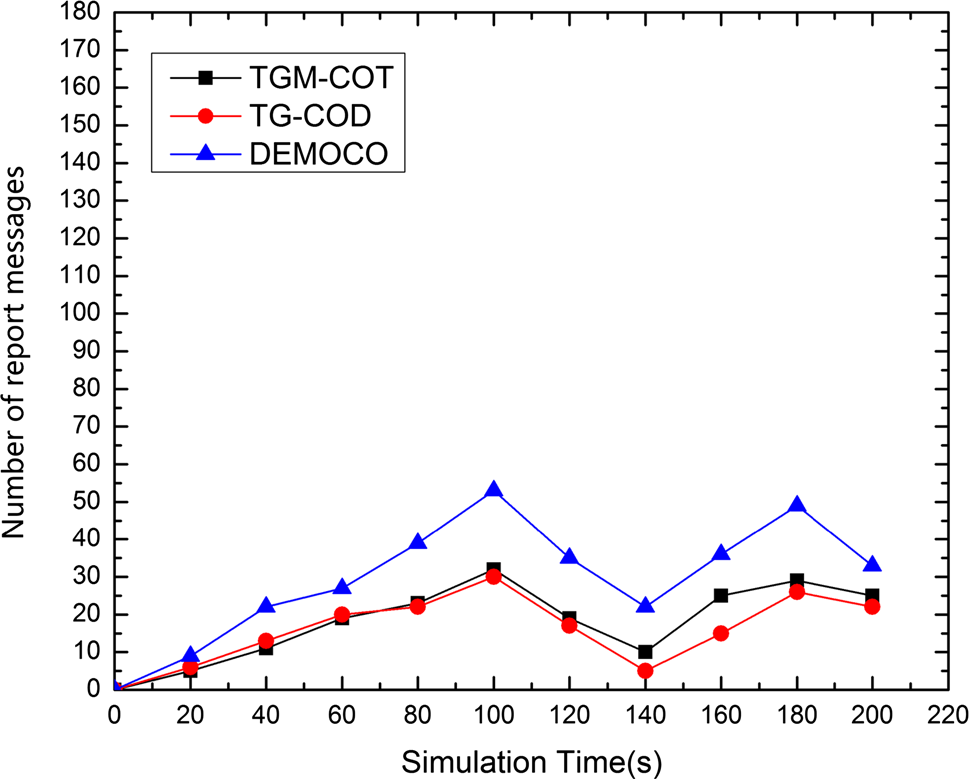
图10比较了三种算法生成的报告消息数量。对于任意给定的时隙，可以看出报告节点数量随目标半径的变化而变化。此外，TGM‐COT在报告节点数量方面始终优于DEMOCO。由于网络结构相似，TGM‐COT与TG‐COD在报告节点数量方面的性能相近。

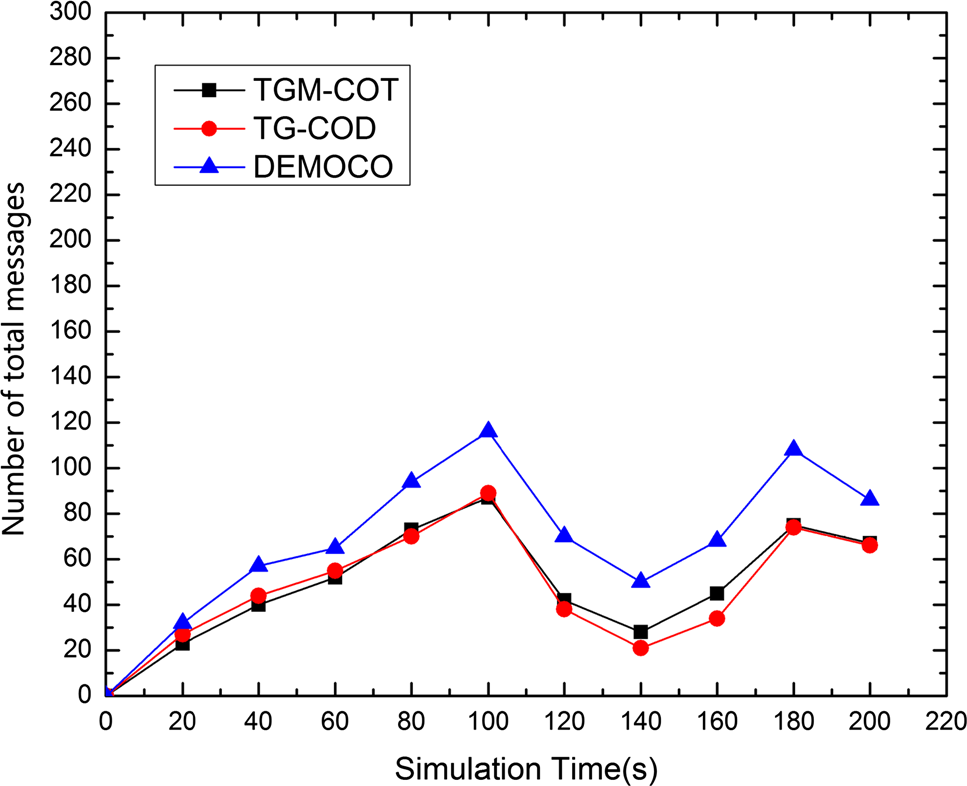
图11显示了总消息数，包括目标跟踪过程中产生的控制消息和报告消息。根据上述分析，每个时隙中交换的消息数量的变化遵循目标覆盖区域的变化。

6.2.4 能耗

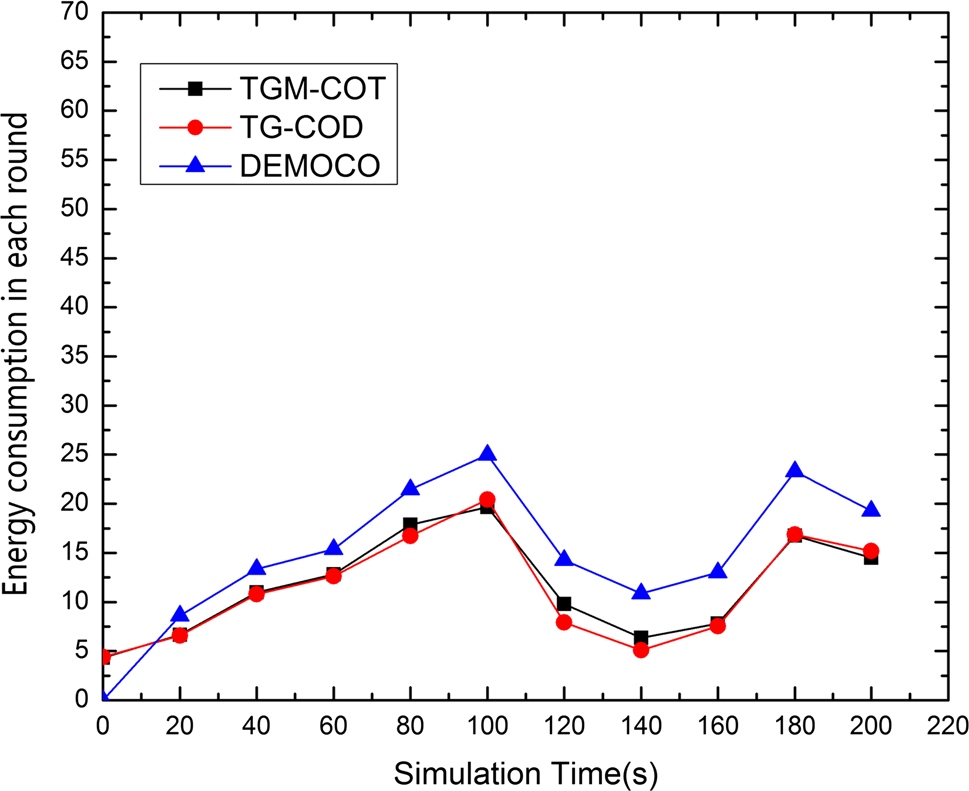
图12展示了每个时隙的能耗。在网络初始化阶段，由于TGM‐COT和TG‐COD中两层网格结构的构建导致的能耗，DEMOCO优于TGM‐COT和TG‐COD。可以看出，在第20个时隙之后，DEMOCO的能耗始终高于TGM‐COT和TG‐COD。在前100个时隙期间，目标发生扩展，导致参与跟踪的节点数量增加。由于每个时隙消耗的能量取决于交换消息的数量，因此随着消息量的增加，能耗也随之上升。在接下来的40个时隙中，目标开始缩小，参与跟踪的节点数量减少，因此此阶段的能耗下降。

图13显示了在200个时隙内的总能耗。由于在TG‐COD中，数据交换消耗能量，并且边界信息是主动收集并发送到汇聚节点时，TG‐COD在总能耗方面略优于TGM‐COT。

6.2.5 跟踪精度

图14展示了节点数量与各算法实现的跟踪精度之间的关系。可以看出，节点密度对跟踪精度的影响较小，而通信范围对跟踪精度影响较大。其原因是，尽管节点密度决定了边界节点的数量，但随着目标的扩展，公式(10)中的累加项 $ \sum_{j=1}^{m} \sqrt{(r(j) - r)^2} $ 也随之增加，从而使 $ e(i) $ 保持动态平衡。另一方面，当通信半径R从5变化到8米时，更多的传感器节点会成为CVN节点的邻居。在这些邻居中，存在远离目标真实边界的边界节点。这种补充增加了 $ e(i) $ 的子部分 $ \sum_{j=1}^{m} \sqrt{(r(j) - r)^2} $。对于TGM‐COT和TG‐COD而言，由于细粒度网格决定了目标边界，节点密度对跟踪精度的影响似乎比通信范围更大。如果能够保持节点密度，跟踪精度将在通信范围变化时保持稳定。然而，随着节点密度的增加，在确定用于边界网格识别的Bratio时产生的误差也会减少。尽管如此，由于采用了类似的双层网格结构和边界节点识别机制，TGM‐COT对节点数量具有较强的鲁棒性。

此外，由于采用了简化机制以消除冗余节点，TGM‐COT在性能上优于其他两种算法。

7 结论

本文针对无线传感器网络提出了一种基于双层网格模型的能量高效连续目标跟踪方案。该方案将监测区域划分为粗粒度和细粒度网格，设计了一种新的边界节点识别机制，并解决了由于节点分布不均导致的边界失真问题。此外，我们提出了候选边界节点选择的精简机制，有助于减少边界节点数量并显著提高跟踪精度。仿真结果表明，TGM‐COT在能量效率和跟踪精度方面优于TG‐COD和DEMOCO。