数据结构——二叉树（二）

一：二叉搜索树

平衡二叉树是在二叉排序树的基础上发展而来的，那为什么要引入二叉搜索树呢？

所谓二叉搜索树（Binary Search Tree），又叫二叉排序树，简单而言就是左子树上所有节点的值均小于根节点的值，而右子树上所有结点的值均大于根节点的值，左小右大，并不是乱序，因此得名二叉排序树。

一个新事物不能凭空产生，那二叉搜索树又有什么用呢？

有了二叉搜索树，当你要查找一个值，就不需要遍历整个序列或者说遍历整棵树了，可以根据当前遍历到的结点的值来确定搜索方向，这就好比你要去日本，假设你没有见过世界地图，你不知道该往哪个方向走，只能满地球找一遍才能保证一定能够到达日本；而如果你见过世界地图，你知道日本在中国的东边，你就不会往西走、往南走、往北走。这种思维在搜索中被叫做“剪枝”，把不必要的分枝剪掉可以提高搜索效率。在二叉搜索树中查找值，每次都会把搜索范围缩小，与二分搜索的思维类似。

定义：二叉搜索树又称二叉查找树，亦称为二叉排序树。

每棵子树头节点的值都比各自左子树上所有节点值要大，也都比各自右子树上所有节点值要小。

二叉查找树的中序遍历序列一定是从小到大排列的。  

                                  

                                                                 左图是二叉查找树，右图不是

查找性能
  当数据数目为N，树高度保持logN附近。则平均查找长度与logN成正比，查找平均时间复杂度为O(logN)。 当先后插入的关键字有序时，二叉搜索树退化成单支树结构。此时树高N。平均查找长度为(N+1)/2，查找的平均时间复杂度为O(N)。
插入性能
  插入效率与查找效率一致。
删除性能
  删除节点时，若节点为叶子节点，或者节点只有单一子树，则时间复杂度为O(1)。若节点既有左子树又有右子树，则需要执行递归过程，对应时间复杂度为O(logN)。

 

二：平衡（二叉）搜索树

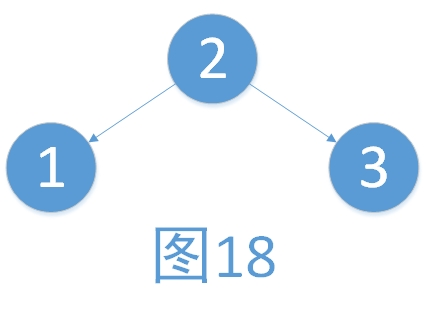
学习过了二叉查找树，想必大家有遇到一个问题。例如，将一个数组{1,2,3,4}依次插入树的时候，形成了图1的情况。有建立树与没建立树对于数据的增删查改已经没有了任何帮助，反而增添了维护的成本。而只有建立的树如图2，才能够最大地体现二叉树的优点。

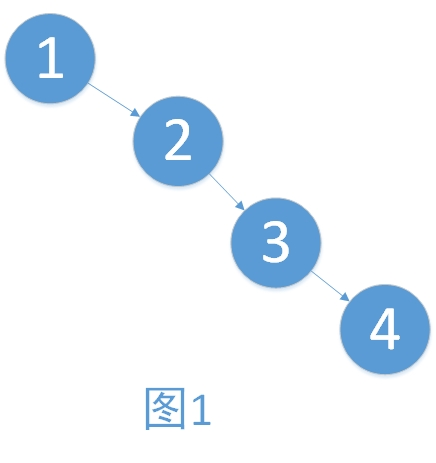
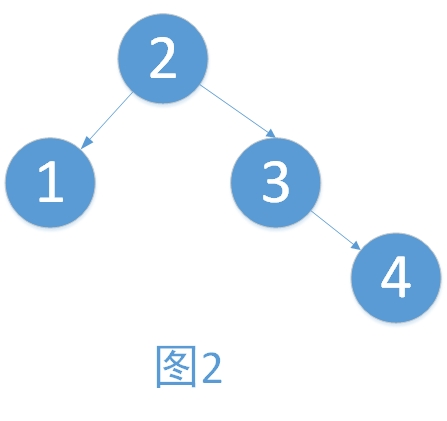
在上述的例子中，图2就是一棵平衡二叉树。科学家们提出平衡二叉树，就是为了让树的查找性能得到最大的体现。

定义：

平衡二叉查找树：简称平衡二叉树。由前苏联的数学家Adelse-Velskil和Landis在1962年提出的高度平衡的二叉树，根据科学家的英文名也称为AVL树。它具有如下几个性质：

1. 可以是空树。
2. 假如不是空树，任何一个结点的左子树与右子树都是平衡二叉树，并且高度之差的绝对值不超过1

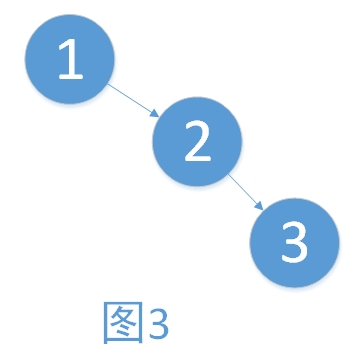
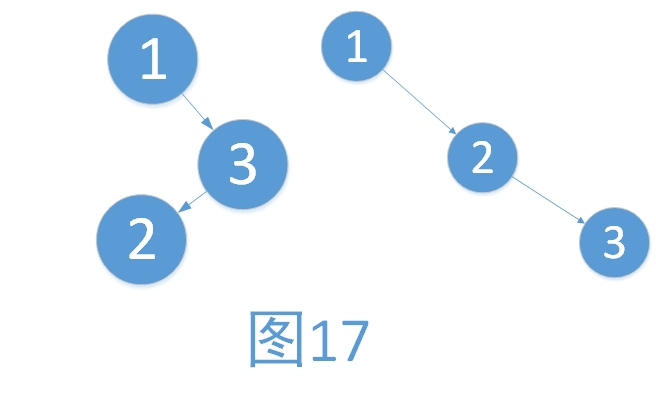
平衡之意，如天平，即两边的分量大约相同。如定义，假如一棵树的左右子树的高度之差超过1，如左子树的树高为2，右子树的树高为0，子树树高差的绝对值为2就打破了这个平衡。如依次插入1，2，3三个结点（如下图）后，根结点的右子树树高减去左子树树高为2，树就失去了平衡。 

平衡因子：左子树的高度减去右子树的高度。由平衡二叉树的定义可知，平衡因子的取值只可能为0,1,-1.分别对应着左右子树等高，左子树比较高，右子树比较高。

                                                                        

平衡二叉树插入时的失衡与调整：平衡二叉树的失衡调整主要是通过旋转最小失衡子树来实现的。

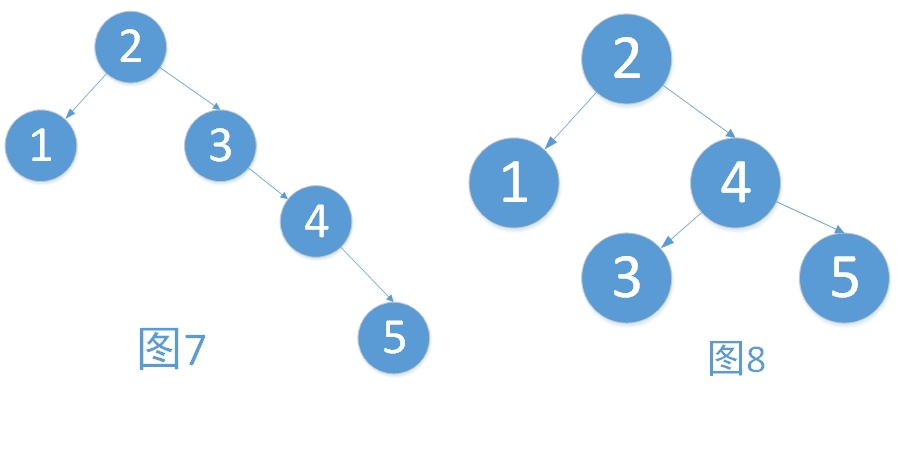
（1）最小失衡子树：在新插入的结点向上查找，以第一个平衡因子的绝对值超过1的结点为根的子树称为最小不平衡子树。也就是说，一棵失衡的树，是有可能有多棵子树同时失衡的，如下。而这个时候，我们只要调整最小的不平衡子树，就能够将不平衡的树调整为平衡的树。

在图7中。2结点（左子树树高-右子树树高）的绝对值=2。同理，3结点的平衡因子也为2.此时同时存在了两棵不平衡子树，而以3为根的树是最小的不平衡子树。我们只要将其以3为中心，将最小不平衡树向左旋转，即可得到平衡二叉树，如图8。

下面我们先用两个简单的例子来感受一下调整的方法。

例1：右子树过高，向左旋转。步骤如下

1. 将2作为根结点
2. 将1作为2的左孩子
3. 将2的左孩子作为1的右孩子（维护树的有序性，只是此处为NULL而已）

                                   

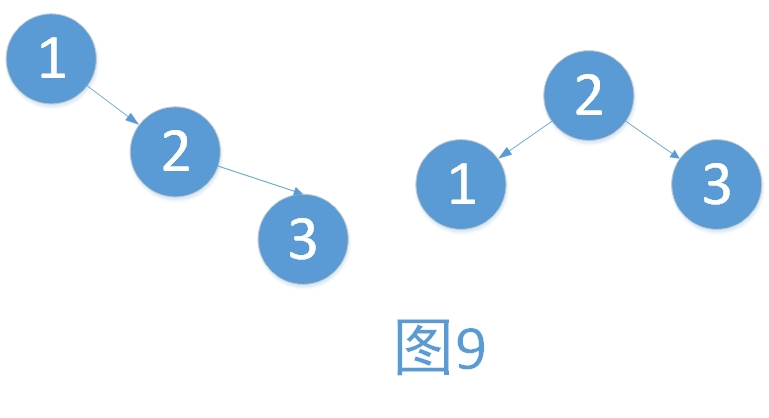
例2：左子树过高，向右旋转。步骤如下

1.      将2作为根结点
2.      将3作为2的右孩子
3.      i将2的右孩子作为3的左孩子（维护树的有序性，只是此处为NULL而已）

                                                        

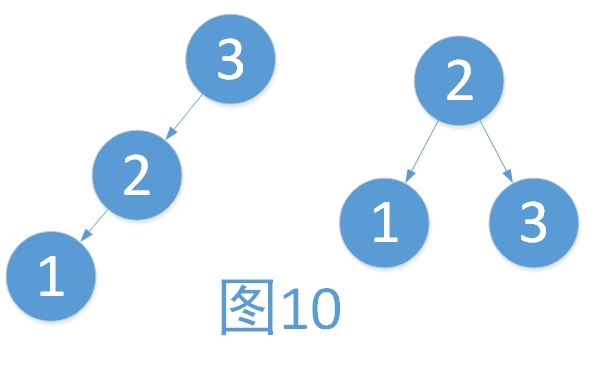
下面我们再来看一个通过旋转，但是没办法达到平衡的失败例子。

例3：右子树过高，向左旋转。步骤如下

1.       将3作为根结点
2.       将3的左孩子作为1的右孩子
3.       将1作为3的左孩子

                                                          

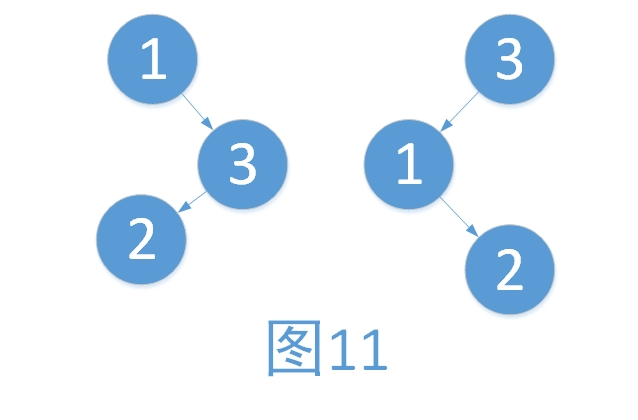
如上，我们发现，旋转之后树并没有恢复平衡。对比图9，我们发现，根的右子树不一致。

　　在上面的三个例子我们可以看出，我们对不平衡的树进行旋转的时候，不仅需要考虑需要最小失衡子树的根结点的平衡因子，还要考虑根结点较高子树的根结点的平衡因子。如图9与图11中，较高子树都为右子树，右子树不同，旋转后有着完全不同的结果。

　　为了方便讨论，我们使用连续的两个字母来表示平衡因子，以表示各种不同的情况。第一个字母表示最小不平衡子树根结点的平衡因子，第二个字母表示最小不平衡子树较高子树的根结点的平衡因子。使用L表示左子树较高，R表示右子树较高，E表示左右子树等高。如上述图11，根为的平衡因子L，较高子树的根为L，我们将这种情况表示为LL型，再如上述例子3，根为R，较高子树的根为L我们将这种情况称为RL型。

　　下面我们将对所有的失衡情况进行讨论。大致分为两大类，一左子树过高，二右子树过高。顺带提一下记忆的方法，读者对于具体某一种类型只要记住最后哪一个结点作为根即可，也就是下面标红色的部分。

二、失衡与处理详解

1. 左子树过高

　　a) LL型

　　在LL型的不平衡树中，我们首先找到最小不平衡子树，再以其根结点向右旋转。为何是向右旋转呢？应该不难理解，向右旋转后，相当于右边的子树树高增加了1，而左边的子树树高降低了1，而原本的树高之差为2,那么就能够将根的平衡因子就化为0.引用一下之前的图如下。旋转之后为“原来根结点的左孩子作为新的根结点”。

　　我们对树以根结点为中心，向右旋转。旋转步骤如下

1.    将2作为根结点
2.    将3作为2的右孩子
3.    将2的右孩子作为3的左孩子（维护树的有序性，只是此处为NULL而已                 

                                 

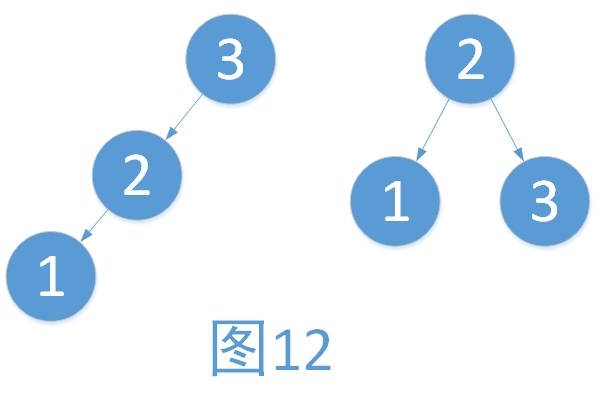
b) LE型

　　在这里需要说明的是，插入的时候，是不会出现LE的这种情况的。只有在删除的时候才会出现。下面对于为何插入不可能出现做一些个人见解。

　　我们不妨假设存在LE的这种情况。如下。

                                                              

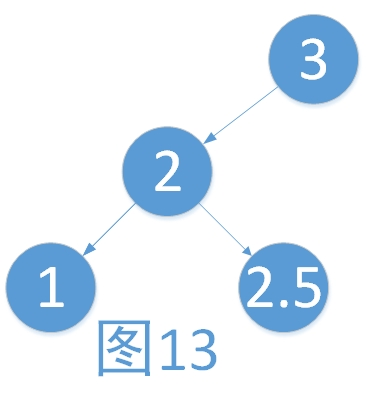
        假设我们刚插入的元素是1，那么原来的树已经不是平衡树。不可能。

　　假设我们刚插入的元素是2.5，那么原来的树也不是平衡树，也不可能。所以说在插入的时候，是不会出现LE的这种情况的。而具体什么时候会出现呢，我们在删除的章节进行讲解。同理，不可能出现RE的情况，下面也不进行讨论。读者可以使用反证法自行验证。

c) LR型

　　对于LR，要分为两步进行旋。旋转之后为“原来根结点的左孩子的右孩子作为新的根结点”。

　　第一以较高子树的根，即1，为中心向左旋转。具体步骤如下。

1.  将2的左子树作为1的右子树（维护树的有序性，只是此处为NULL而已）
2.  将1作为2的左子树
3.  将2作为3的左子树

                                                                  

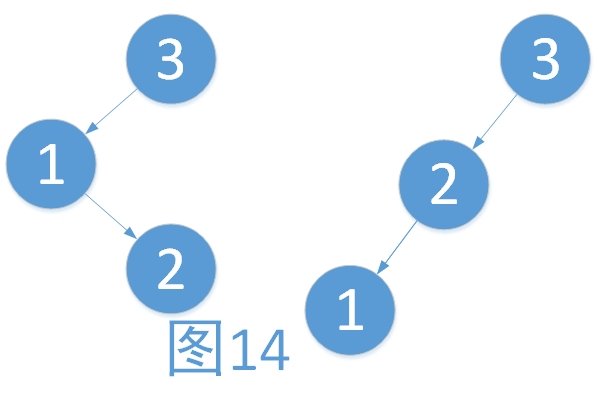
　　第二以原树的根，即3为中心，向右旋转。最后结果如下

                                                                         

 

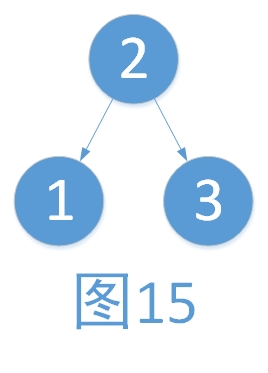
2. 右子树过高

　　a) RR型

　　还是引用一下之前的例子。旋转的步骤如下。旋转之后为“原来根结点的右孩子作为新的根结点”。

     i.  将2作为根结点

    ii.  将1作为2的左孩子

   iii.  将2的左孩子作为1的右孩子（维护树的有序性，只是此处为NULL而已）

                                                          

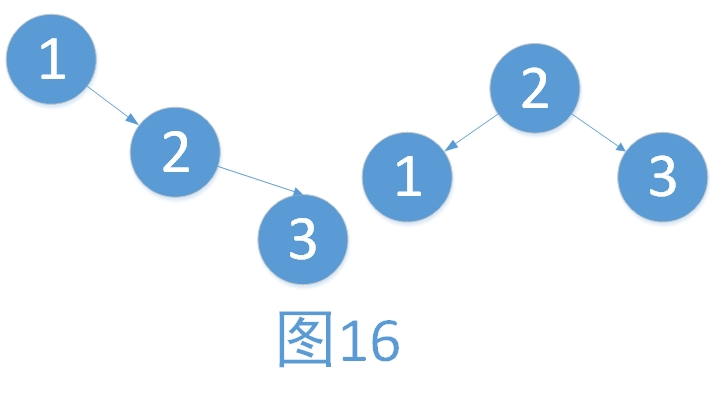
　　最后1,2,3的平衡因子都为EH。

　　b)RL型

　　还是引用一下之前的例子。与LR型类似，我们需要进行两次旋转。旋转之后为“原来根结点的右孩子的左孩子作为新的根结点”。

　　第一，以根结点的右孩子即3为中心向右旋转，结果如下。具体步骤如下

      i.  将2作为1的右孩子

     ii.  将3作为2的右孩子

    iii.   将2的右孩子作为3的左孩子（维护树的有序性，只是此处为NULL而已）

                                               

　　第二，以原根结点即1，作为中心，向左旋转。结果如下。具体步骤如下

     i.   将2作为根结点

    ii.   将1作为2的左孩子

   iii.   将2的左孩子作为1的右孩子（维护树的有序性，只是此处为NULL而已）

 　　　　　　                                            

3、  插入时失衡与调整的总结

1. 在所有的不平衡情况中，都是按照“寻找最小不平衡树”->“寻找所属的不平衡类别”->“根据4种类别进行固定化程序的操作”。
2. LL,LR，RR，RL其实已经为我们提供了最后哪个结点作为新的根指明了方向。如LR型最后的根结点为原来的根的左孩子的右孩子，RL型最后的根结点为原来的根的右孩子的左孩子。我们只要记住这四种情况，可以很快地推导出所有的情况。
3. 维护平衡二叉树，最麻烦的地方在于平衡因子的维护。想要熟悉这个过程，建议读者多多画图，在感官上首先体验这个过程。