DM2-ECOP：多用户多云卸载策略

DM2‐ECOP：一种面向多用户多云朵移动边缘计算环境的高效计算卸载策略

1 引言

移动云计算范式已被提出，以允许在云中远程执行资源密集型移动应用。应用程序的计算随后被传输到远程云进行处理。该操作被称为计算卸载[6, 7]。然而，云与用户之间的地理距离可能引入较大且不稳定的延迟，这会显著降低延迟敏感型应用的用户体验，例如移动游戏、增强现实以及人脸识别和语音识别[8, 30]。为解决此类问题，移动边缘计算（MEC）作为一种主要范式应运而生，旨在在网络边缘提供云计算能力，以支持对延迟敏感的移动应用。其核心概念依赖于在网络边缘部署称为云小站的小型服务器集群[11, 18]。用户随后可将计算任务卸载到更近的云小站。

在多用户环境中，多个移动设备可能会竞争将计算任务卸载到云小站。因此，卸载策略的性能在很大程度上取决于云小站的计算资源共享以及无线带宽分配策略[4, 5, 12]。此外，在多云朵MEC环境中，当用户周围存在多个可用的云小站时，计算卸载的性能还依赖于云朵选择[14, 33, 34]。

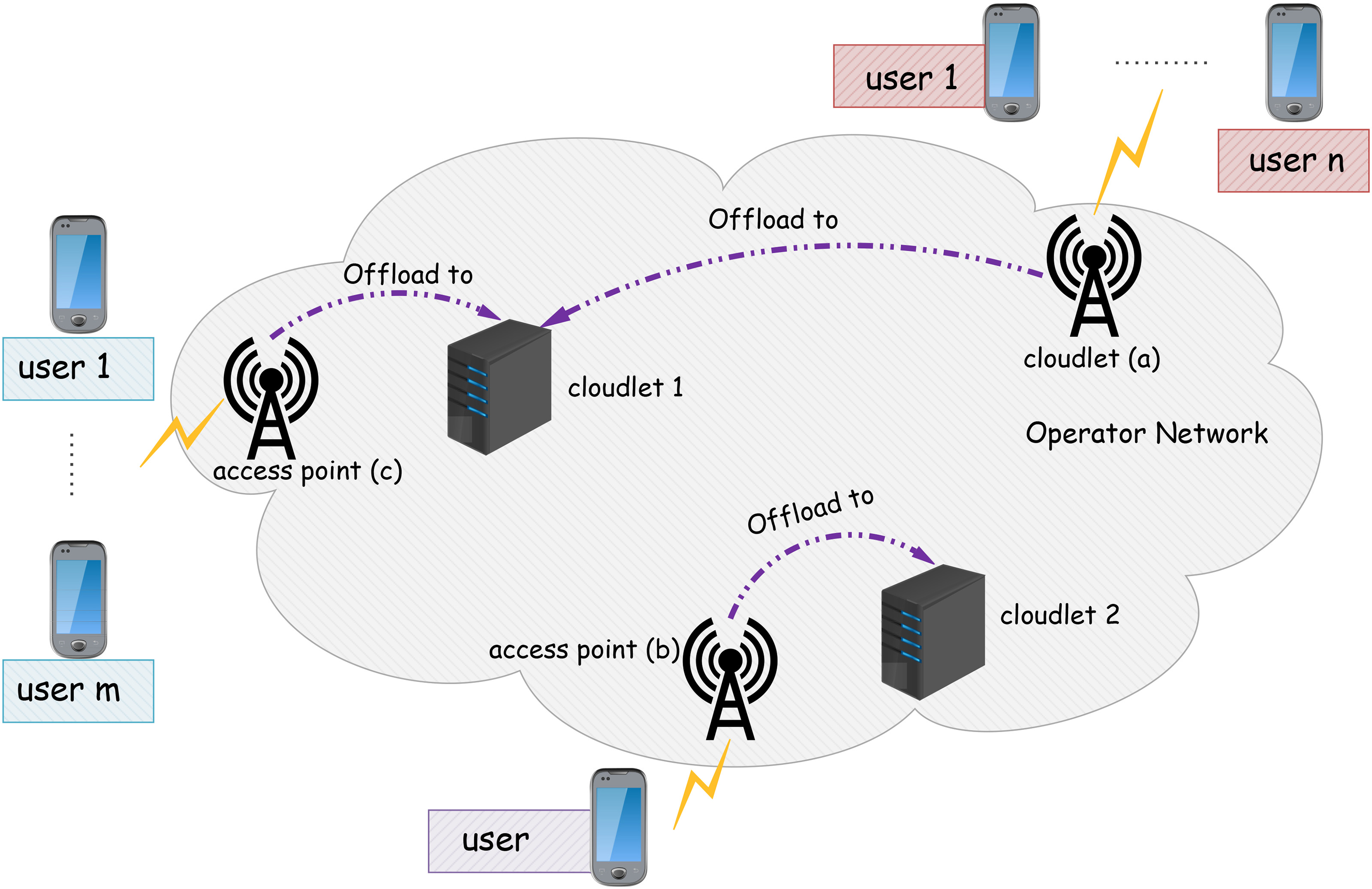
许多近期的研究探讨了云朵选择问题[21, 27, 34]。大多数已提出的卸载策略依赖于用户密度，以将每个区域静态分配给一个云小站[15, 27]。因此，如图1所示，同一区域内的用户将始终卸载到同一个云小站。然而，用户的动态密度可能导致云小站之间的负载不平衡，从而造成MEC容量次优使用和更长的卸载延迟。因此，为了实现高性能，卸载策略必须同时考虑带宽分配、计算资源分配和云朵选择。

为了解决这一问题，本文研究了多用户、多云小站多接入边缘计算环境中的计算卸载。我们的目标是提供一种高效的卸载策略，该策略为每个用户确定最佳的卸载决策和云朵选择，以降低总卸载成本。

本文提出了一种新的计算卸载策略，名为分布式多用户多云小站高效计算卸载策略（DM2‐ECOP），旨在提升MEC环境中的卸载性能。该策略扩展了参考文献[4, 5, 12]中提出的卸载策略。与以往研究类似，我们假设每个用户一次仅执行一个应用程序。然而，不同于这些研究，我们将MEC支持的应用程序分为两类：（1）必须在远程执行的应用程序；（2）可根据执行时的条件选择在本地或远程执行的应用程序。DM2‐ECOP致力于根据网络和系统资源可用性选择最优云小站，同时最小化卸载成本。卸载成本定义为移动设备消耗的能量与所有应用程序完成时间的总和的组合。

我们将该计算卸载问题建模为混合二进制规划问题，然后采用基于分布式线性松弛的启发式方法进行求解，该方法遵循拉格朗日分解思路。DM2‐ECOP包含两个决策层级：（1）本地卸载管理器负责处理同一接入点内的关联用户，并求解与此接入点相关的卸载子问题；本地卸载管理器使用我们提出的算法——贪心最优云小站优先选择启发式（GBC‐SFH），该算法为每个应用程序选择最优云小站进行卸载，以最小化能耗和完成时间。（2）在第二层级，全局卸载管理器确保各本地卸载管理器分配给云小站的资源满足每个云小站的容量约束。

本文其余部分组织如下：第2节介绍计算卸载领域的现有工作。第3节介绍系统建模。多用户、多云朵卸载问题在第4节中进行形式化表述。我们的卸载策略DM2‐ECOP在第5节中详细说明。性能评估在第6节中进行详细分析。最后，第7节给出结论。

2 相关工作

许多研究被提出以探索计算卸载，从而提升移动设备的性能。然而，并非所有提出的卸载策略都具有相同的目标。下文我们将区分三个主要目标：（i）卸载决策，（ii）云朵部署，以及（iii）云朵选择。

一些已提出的工作研究了卸载决策，以确定哪些计算应卸载到远程云，例如：Meng‐Hsi Chen等人[4], Xu Chen等人[5], Songtao Guo等人[12], 盖克克等人[10], 毛玉仪等人[22], 以及黄东等人[13]。Meng‐Hsi等人是最早研究移动云计算中多用户计算卸载的团队之一。所提出的卸载策略确定哪些计算必须在远程云上执行，哪些必须由移动设备本地执行。然后，该策略为每个用户分配无线带宽，以降低移动设备的能耗。

Xu Chen等人的卸载策略是为单个云小站MEC环境设计的。每个用户根据可用的无线带宽尝试卸载其计算任务，以减少能耗。Songtao Guo等人提出了另一种多用户卸载方法。与DM2‐ECOP类似，该工作将卸载成本最小化，该成本定义为能耗和处理时间的组合。该卸载策略决定哪些计算可以被卸载，并为每个卸载任务分配无线带宽和处理器频率。

计算方面，盖克克等人提出了一种调度器，用于在本地移动设备和远程云之间分配任务，以节省能耗。毛玉仪等人提出了一种卸载策略，尝试在多用户场景下将计算卸载到边缘服务器或云小站。该策略为每个用户分配CPU频率和带宽，以降低移动设备的能耗。最后，黄东等人设计了一种针对单用户场景的计算卸载策略，以减少移动设备的能耗。他们专注于部分卸载，即卸载策略在运行时对应用程序进行划分，以确定哪些计算必须在本地执行，哪些必须卸载到远程服务器。尽管这些策略都提升了移动设备的性能，但它们依赖于云的无限容量。因此，这些策略需要进一步改进，才能适用于计算资源有限的云小站的多接入边缘计算环境。

南玉辰等人[25, 26]和周崇宇等人[35]提出了计算卸载策略以降低雾节点的能耗。他们引入了一种卸载策略，其中雾节点尝试将其计算任务卸载到远程云。对于每个雾节点，该策略决定哪些计算必须卸载到远程云，哪些必须由节点本地执行。在文献[26],中，该卸载策略已被扩展以减少应用程序的完成时间。类似地，周崇宇等人提出了一种在线卸载策略，该策略可以选择应由最近的云小站执行的计算任务，以最小化系统范围效用，即执行时间。与这些旨在降低雾服务器能耗的策略不同，DM2‐ECOP侧重于降低移动设备端的卸载成本。此外，物联网设备的计算能力极弱，无法运行任何应用程序，而移动设备则具备较强的计算能力，能够运行复杂应用程序。

云朵部署也是MEC面临的一个挑战性问题，许多近期的研究提出了在MEC环境中的一些云朵部署启发式方法。Mike Jia等人[14, 33], 姚红等人[34], 以及马龙杰等人[21]在多用户、多云点MEC环境中引入了云朵部署与选择算法。Mike Jia等人的卸载方法是大规模环境中云朵部署的首批启发式方法之一。其主要目标是在大规模网络中找到最优的云小站部署位置，然后为每个AP选择一个云小站来执行计算任务。采用基于用户密度的K‐中值聚类方法来部署云小站。随后，每个AP被静态分配到一个云小站。类似地，姚红等人设计了支持异构云朵环境的启发式方法。最后，马龙杰等人提出了一种启发式方法，旨在确定必须部署的最少数量的云朵，以改善大规模网络中的用户体验质量。在多用户MEC环境中，移动用户的密度是动态变化的。因此，将AP静态分配给云小站可能会降低计算卸载的性能。为了避免这一问题，我们的DM2‐ECOP方法考虑了动态云点选择和无线带宽分配，旨在最小化能耗并提升移动设备的性能。

其他研究尝试在多云点MEC环境中寻找动态云点选择。Anwesha Mukherjee等人[24, 27], Mike Jia等人[15], 朱其亮等人[36], 以及Arash Bozorgchenari等人[2]提出了支持动态云点选择以降低卸载成本的方法。Anwesha Mukherjee等人设计了一种多级卸载策略以优化能耗。用户首先将任务卸载到最近的云点。根据该云点中的资源可用性，它可以执行任务或将任务卸载到另一个云点。Mike Jia等人提出了一种启发式方法来平衡云朵之间的负载。其主要目标是将部分计算从过载的云朵迁移到负载较轻的云朵，以减少执行时间。类似地，朱其亮等人开发了一种两级卸载策略，其中移动设备根据资源可用性将其计算任务卸载到卸载服务器。他们使用了

决定在本地云朵执行计算还是将计算卸载到远程云的代理。Arash Bozorgchenani等人提出的卸载策略试图选择一个附近的雾节点，将繁忙雾节点的部分计算卸载过去，以节省能耗和完成时间。尽管这些工作提出了动态云朵选择启发式方法，任务仍然总是被卸载到最近的云点，由该云点决定是本地执行还是传输给其他云朵。因此，产生了额外的卸载成本，从而导致卸载性能下降。在我们的方案中，每个被卸载任务所执行的云朵将在卸载决策时确定，且不产生额外成本。

上述所有卸载策略都致力于降低卸载成本。它们将计算卸载到预设的远程服务器（远程云或本地云朵）。远程服务器的选择在开发阶段基于用户密度等指标静态完成，尽管用户密度会随时间动态变化。此外，云小站的计算能力有限，无法执行所有卸载的计算任务。为避免这种情况，文献中最常采用的策略是考虑两层架构：任务首先卸载到最近的云点，当该云小站过载时，再将其部分计算卸载到另一个云小站或远程云。尽管两层卸载策略可以提升卸载方法的性能，但会带来额外的卸载成本。此外，在多云朵场景中，用户周围存在多个可用云小站，始终选择同一个云小站并非最佳策略。因此，本文提出一种新的卸载策略，以提高多接入边缘计算环境中计算卸载的效率。该新策略必须考虑多个可供用户卸载计算的云小站，并计算最优的计算分配方案，以优化卸载成本。

3 系统描述

在本节中，我们描述了我们的系统建模。首先介绍MEC模型，然后提出通信与计算卸载模型。最后，将卸载成本作为优化问题的目标函数。表1列出了本文中用于建模多用户、多云朵计算卸载问题的变量和符号。

3.1 MEC环境模型

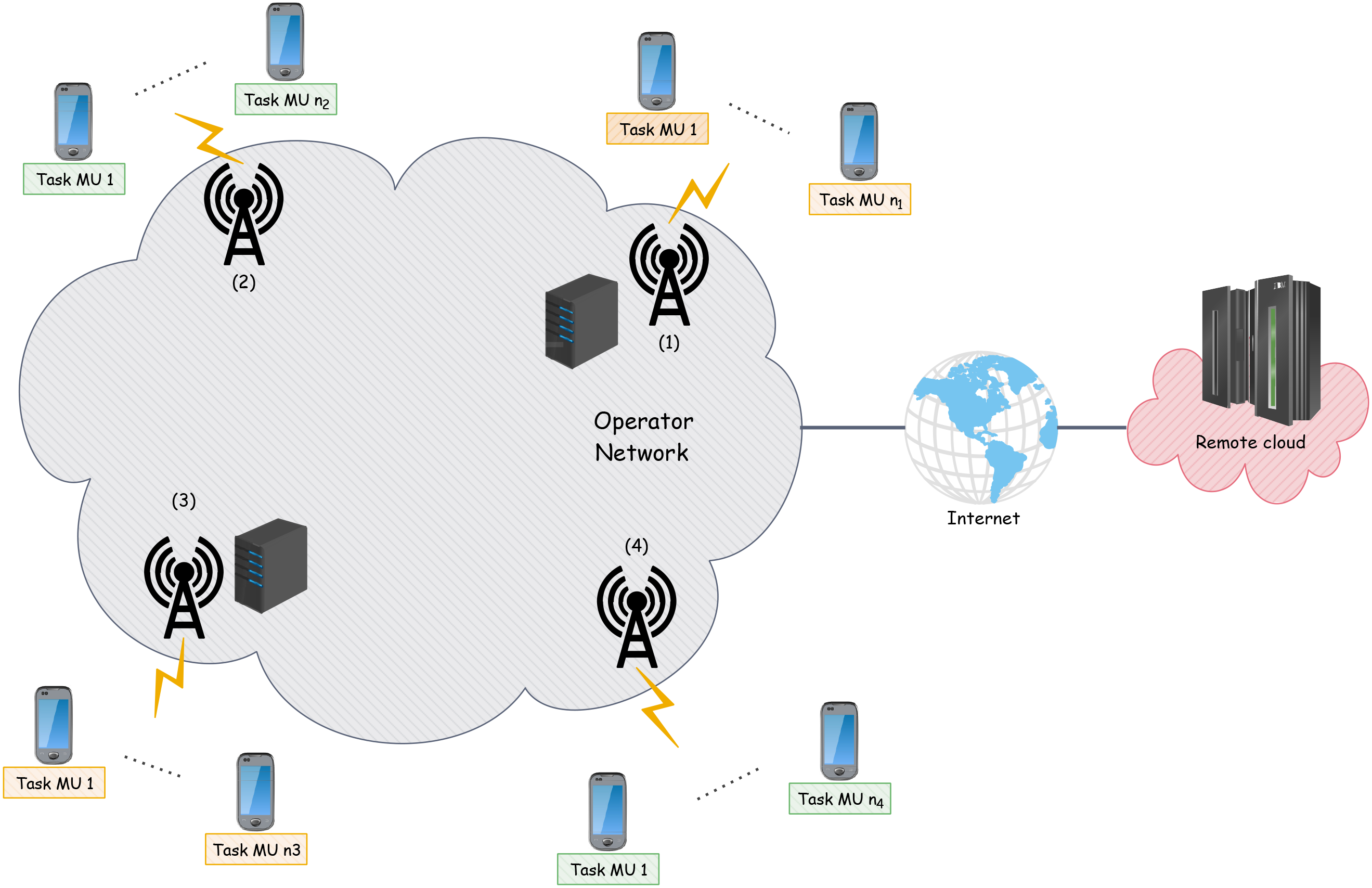
让我们考虑一个由M个接入点和K个云小站组成的多接入边缘计算环境，如图2所示。我们假设云小站的数量少于接入点的数量（K ≤ M）。在本文中，我们假设云小站已经部署完毕，并且与接入点共址。同时，我们假设用户可以通过其接入点与云小站进行通信。下文中，我们将接入点的集合表示为 M={1, 2,…, M}，并假设每个接入点i关联有Ni个用户。设 Nm={1, 2,…, Nm}为与第m个AP关联的用户的集合， K={1, 2,…, K}为云小站的集合。我们还定义um, n为第m个AP的第n个用户。类似于现有研究，每个用户在其移动设备上运行一个应用程序。该应用程序具有以下特征：（i）以CPU周期表示的计算资源需求，记为γ u m,n；（ii）上传至多接入边缘计算的数据量，记为upu m,n；（iii）在多接入边缘计算上执行结束后需要从多接入边缘计算下载到用户的数据量，记为dwu m,n；（iv）最后，根据应用程序所需的服务质量（QoS）所规定的最大容忍延迟，记为tum,n。

如先前的研究所述[11, 19], 我们将计算卸载应用程序分为两类：（1）静态卸载决策任务和（2）动态卸载决策任务。在第一类中，应用程序在设计时预先划分：本地部分（任务）始终在移动设备上执行，远程部分（任务）始终在远程执行。如图3(a)所示，任务的源代码已存在于远程服务器中，因此移动设备只需将输入数据传输到远程服务器。典型的静态卸载决策任务示例是安卓平台上的FLUID应用[16]，该应用用于粒子模拟。FLUID的轻量客户端在移动设备上运行，而服务器部分必须在多接入边缘计算环境中远程执行，因为它需要高性能的GPU计算处理器，而这些处理器在移动设备中并不常见。

在第二类中，应用程序需要根据网络和多接入边缘计算资源可用性在运行时进行相应划分。通常情况下，移动终端需要决定是在本地执行任务，还是将全部或部分任务进行卸载。在这种情况下，如图3(b)所示，当任务被卸载时，移动设备必须传输其源代码和输入数据。这类应用程序的一个示例是安卓平台的Linpack基准测试[32]，旨在测量安卓设备的性能。该应用程序可以完全在移动终端上执行，也可以部分卸载到云小站。

为简化分析，本文将静态卸载决策任务和动态卸载决策任务均建模为具有卸载计算比例的任务，记为aum ,n。其中， aum ,n表示应用程序中需要在远程执行的计算比例。区分静态卸载决策任务和动态卸载决策任务，我们考虑对于静态卸载决策任务，其卸载比例始终等于1，这意味着属于该类别的任务总是被卸载。本地部分视为等于零，因为它不会影响系统性能，因为该部分始终应在终端执行。然而，对于动态卸载决策任务，此卸载计算比例可以在0到1之间取任意值（即aum ,n ∈[0, 1]）。此外，为简化起见（但不失一般性），我们还假设当一个任务以给定的卸载计算比例进行卸载时，需要传输的数据量也与该比例成正比。但是，无论aum ,n的值如何，任务的输出（记为dwu m,n）保持不变。

为了表明用户um, n的应用程序属于哪一类，我们引入了二进制变量y u m,n，其对于静态卸载决策任务取值为1，对于动态卸载决策任务取值为0。

最后，由于任务对硬件和软件的约束，我们假设某些云小站无法执行某些任务。在这种情况下，我们定义第二个二进制变量дum,n,k，用于表示云小站k是否能够执行该任务。因此，дum,n,k在第k个云小站能够执行该任务时等于1，否则为0。

3.2 通信模型

设G=(V, E)为一个加权图，其中V(M ∪K)是对应于接入点和云小站集合的有限顶点集， E是表示任意两个顶点之间可能通信的连接（边）的集合。我们还考虑边的权重，记为ei,j，表示每两个顶点i和j之间的网络延迟。因此，利用Dijkstra算法，我们可以计算一个延迟矩阵，记为Dm, k，表示第m个AP与第k个云小站之间的延迟。根据上述考虑，我们可以按如下方式估计分配给每个用户的带宽：

$$ w_{um,n} = \frac{W_m(\pi_m)}{\pi_m} $$ (1)

其中πm是卸载容量，表示卸载其应用程序到多接入边缘计算的用户数量，如定义5.1所述。Wm（πm）是第m个AP与其关联的用户之间共享的带宽。为了估计该带宽，我们考虑了比安奇模型[1, 20]。

根据之前的假设，我们可以计算任意任务的通信时间。该时间记为T t um,n,k，由从用户终端向云小站上传数据所需的时间以及任务完成后从云小站下载结果所需的时间组成。在这种情况下，T t um,n,k可以表示为：

$$ T^t_{um,n,k} = \frac{a_{um,n} \cdot up_{um,n}}{w_{um,n}} + D_{m,k} + \frac{dw_{um,n}}{w_{um,n}} + D_{m,k} = \frac{a_{um,n} \cdot up_{um,n} + dw_{um,n}}{w_{um,n}} + 2D_{m,k} $$ (2)

3.3 计算处理模型

a) 本地处理：我们假设用户设备具有用于任务计算的本地计算能力fum,n。当用户将其计算的百分比aum,n卸载后，剩余部分必须在本地执行。因此，本地部分的本地处理时间可估计为：

$$ T^l_{um,n} = \frac{(1 - a_{um,n}) \cdot \gamma_{um,n}}{f_{um,n}} $$ (3)

从上述公式可以看出，由于静态卸载决策任务的aum ,n恒等于1，因此静态卸载决策任务的本地处理时间等于零（T l u m,n = 0）。

b) 远程处理：对于远程计算，我们假设每个云小站具有F k的计算能力。每个云小站分配其部分计算资源以执行卸载的任务。因此，用户um的 n任务的远程执行时间可估计为卸载计算的资源与所分配计算资源的比值，如以下公式所示：

$$ T^e_{um,n,k} = a_{um,n} \cdot \frac{\gamma_{um,n}}{c_k} $$ (4)

其中ck是分配给在kth云小站执行任务的计算资源量。为了简化模型，我们假设每个云小站分配的计算资源是固定的，在计算过程中不会发生变化[4, 5, 12]。

3.4 卸载成本模型

我们将卸载成本定义为应用程序的能耗和执行时间的组合。接下来，我们将介绍本地卸载成本和远程卸载成本。

a) 本地卸载成本：根据上述考虑，本地卸载成本表示为任务的能耗和执行时间的组合，如下所示：

$$ Z^l_{um,n} = \beta_{um,n} \cdot E^l_{um,n} + (1 - \beta_{um,n}) \cdot T^l_{um,n} $$ (5)

其中，E l um,n和T l um,n分别表示用户um, n的应用程序本地部分的总能耗和总处理时间。βum,n表示用户卸载决策中执行时间和能耗的权重参数。当用户设备的电池处于低电量状态，且需要降低能耗时，可设置βum,n= 1；然而，当运行延迟敏感型任务时，用户可设置βum,n= 0，以赋予执行时间更高的优先级。为了获得更灵活的成本模型，我们通过考虑能耗、执行时间或二者组合，允许采用多准则卸载策略。

考虑到能耗模型，本文采用参考文献[3, 23]中提出的模型。利用该模型，我们可以按如下方式计算E l um,n：

$$ E^l_{um,n} = \kappa \cdot (f_{um,n})^3 \cdot T^l_{um,n} $$ (6)

其中 κ是有效开关电容，其取决于芯片架构，并用于调节处理器频率。下文中，我们将 κ= 10−9设为如[3, 23]所示。

b) 远程卸载成本：用户终端远程执行任务所消耗的总能量等于设备将无线电模块置于传输模式以向远程服务器发送数据时消耗的能量，加上设备将无线电模块置于空闲模式以等待任务完成时消耗的能量，再加上设备再次将无线电模块置于接收模式以从远程服务器接收结果数据时消耗的能量。该消耗能量可表示如下：

$$ E^e_{um,n,k} = P^{tx/rx} {um,n} \cdot (T^t {um,n,k} - 2D_{m,k}) + P^{idle} {um,n} \cdot (T^e {um,n,k} + 2D_{m,k}) $$ (7)

其中P tx/rx u m n ，是无线电模块处于发送或接收模式时的功耗，而P idle u m ， n是无线电模块处于空闲模式时的功耗[3, 23, 29]。

最后，我们可以将远程卸载成本定义如下：

$$ Z^e_{um,n,k} = \beta_{um,n} \cdot E^e_{um,n,k} + (1 - \beta_{um,n}) \cdot (T^t_{um,n,k} + T^e_{um,n,k}) $$ (8)

4 多用户、多云朵计算卸载问题的建模与分解

为了提出一种高效的卸载策略，我们将该问题建模为一个优化问题。然后，我们采用拉格朗日松弛方法将问题分解为多个子问题，并分别求解每个子问题。

4.1 问题描述

如前所述，本文的目标是提出一种高效的卸载策略。该策略决定哪些用户应将其任务进行卸载、确定需卸载的计算量，并为每个用户选择一个云小站，同时最小化总卸载成本。设 xum,n,k表示第n个用户在第m个AP上的任务到云小站k的卸载决策，即当用户um, n将任务卸载到云小站k时，xum,n,k= 1为1，否则为0。基于系统描述以及服务质量和云小站资源能力约束，该问题可表述如下：

Minimize
$$ \sum_{m}^{M} \sum_{n}^{Nm} Z_{um,n} $$

Subject to:
C1: $$ \sum_{k=1}^{K} x_{um,n,k} \leq 1, \forall m \in M, u_{m,n} \in N_m $$
C2: $$ y_{um,n} - \sum_{k=1}^{K} x_{um,n,k} \leq 0, \forall m \in M, u_{m,n} \in N_m $$
C3: $$ T_{um,n} \leq t_{um,n}, \forall m \in M, u_{m,n} \in N_m $$
C4: $$ x_{um,n,k} \leq д_{um,n,k}, \forall m \in M, u_{m,n} \in N_m, k \in K $$
C5: $$ \sum_{m} \left( \sum_{n} x_{um,n,k} \cdot c_k \right) \leq F_k, \forall k \in K $$
C6: $$ x_{um,n,k} \in {0, 1}, \forall m \in M, u_{m,n} \in N_m, k \in K $$
C7: $$ a_{um,n} \in [0, 1], \forall m \in M, u_{m,n} \in N_m $$
C8: $$ a_{um,n} \geq y_{um,n}, \forall m \in M, u_{m,n} \in N_m $$ (9)

其中Zu m,n是用户um, n任务的卸载成本。Zu m,n可用以下公式表示：

$$ Z_{um,n} = Z^l_{um,n} + \sum_{k=1}^{K} x_{um,n,k} \cdot Z^e_{um,n,k} $$ (10)

如问题公式化所示，我们的目标是最小化网络中用户的总卸载成本。第一个约束（C1）确保每个任务最多被分配到一个云小站。约束（C2）保证任何静态卸载决策任务必须恰好分配到一个云小站，而动态卸载决策任务最多可分配到一个云小站。下一个约束（C3）表明，任务所需的QoS（以完成时间衡量）必须小于给定的阈值。该阈值基于移动应用的特性得出[5, 7]。例如，对于交互式应用，用户感知——从提交任务到接收到响应的时间间隔——是一种常用的技术来

确定阈值[8]。完成时间可表示如下：

$$ T_{um,n} = T^l_{um,n} + \sum_{k=1}^{K} x_{um,n,k} \cdot (T^t_{um,n,k} + T^e_{um,n,k}) $$ (11)

下一个约束（C4）确保每个被卸载的任务必须由满足该任务所需硬件和软件的云小站执行。C5约束表明，不能超过每个云小站的计算能力。约束C6确保任何决策变量均为二进制变量。

最后，约束（C7）表示卸载计算的比例必须是介于0和1之间的实数值。而（C8）确保每个静态卸载决策任务必须始终完全卸载。

定理4.1. 方程(9)是一个包含指数函数和约束的非线性混合二进制问题(NLMBP)。它是一个NP难问题。

证明。 考虑一种特殊情况，其中每个接入点关联的用户数量相同，且所有任务均为静态卸载决策。因此，所有任务必须卸载到云小站，并且分配给每个用户的带宽已预先确定。此时，该特殊情况是一个线性二进制整数问题(LBIP)。实际上，此特殊情况可轻易归约为带有分配限制的广义分配问题(GAP)，而该问题是NP难问题，如参考文献[17]所示。由于该特殊情况是NP难问题，故方程(9)也是NP难问题。

考虑到该问题的NP难问题性质，很难获得最优解。接下来，我们使用拉格朗日松弛和分解方法提出方程(9)的一个简化版本。

4.2 问题分解

为了解决上述问题，我们需要一种分解方法。将一个复杂的优化问题分解为若干个较小的问题，称为子问题，并分别求解每个较小的问题。不幸的是，约束C5被视为一个复杂约束[9, 31],，因为它涉及多个子问题的局部变量。因此，方程(9)的分解无法一步完成，且子问题无法独立求解。对于这类复杂问题，存在高级分解技术，通过迭代求解一个子问题序列来解决。本文中，我们采用其中一种最流行的分解技术——拉格朗日松弛[9, 31]。拉格朗日松弛的思想源于使用拉格朗日乘子对问题进行分解；因此，我们在约束C5上引入拉格朗日乘子 λ=[λk, k ∈ K] T，其中λk表示由kth号云小站执行的所有任务的价格。X和A分别是卸载决策变量的集合和卸载比例的集合。拉格朗日函数定义如下：

$$ L(X, A, \lambda) = \sum_{m}^{M} \sum_{n}^{Nm} Z_{um,n} + \sum_{k} \lambda_k \left( \sum_{m} \sum_{n} (x_{um,n,k} \cdot c_k - F_k) \right) $$

$$ = \sum_{m}^{M} \sum_{n}^{Nm} Z_{um,n} + \sum_{m} \sum_{n} \sum_{k} \lambda_k x_{um,n,k} \cdot c_k - \sum_{k} \lambda_k F_k $$

$$ = \sum_{m}^{M} \sum_{n}^{Nm} \left( Z_{um,n} + \sum_{k} \lambda_k x_{um,n,k} \cdot c_k \right) - \sum_{k} \lambda_k F_k $$

原始方程（9）的拉格朗日对偶问题如下所示：

$$ \max_{\lambda} \min_{X,A} L(X, A, \lambda) $$

我们可以看到，拉格朗日对偶问题可以分解为两个层级：第一级是内层最小化，包含M个子问题，每个子问题仅涉及一个接入点。第二级是外层最大化，即主问题，它考虑全局变量和约束C5。

基于这一观察，我们提出了一种新的卸载策略，称为分布式多用户、多云朵高效计算卸载策略（DM2‐ECOP）。下文将描述所提出的计算卸载策略。

5 DM2‐ECOP：分布式多用户、多云朵高效计算卸载策略

如上一节所述，拉格朗日对偶问题可分解为M个子问题。每个子问题试图为其关联的接入点所对应的用户找到最优的卸载决策和云朵选择。基于这一特性，我们设计了一种新的卸载策略DM2‐ECOP。如图4所示，DM2‐ECOP具有两个决策层级。本地卸载管理器负责一个接入点的卸载决策和云朵选择；它求解相应的子问题，然后将卸载决策和云朵选择结果发送至集中式决策层级。MEC计算卸载管理器接收所有子问题的解，并确保所得到的卸载方案是可行的且满足所有约束条件。随后，它更新拉格朗日乘子，并将新的值传送给每个本地卸载管理器以优化局部解。

5.1 本地卸载管理器：一种基于最优云小站优先选择的贪心启发式方法（GBC‐SFH）

本地卸载管理器尝试解决一个接入点的子问题，以决定哪些用户可以进行卸载。然后，它选择合适的云小站来执行每个用户的任务。根据之前的考虑，我们可以将本地卸载管理器的子问题表述为

如下：

Minimize $$ \sum_{n}^{Nm} \left( Z_{um,n} + \sum_{k} \lambda_k x_{um,n,k} \cdot c_k \right) $$

受限于：
constraints C1 – C4 and C6–C8. (12)

为了解决该子问题，我们需要知道分配给每个用户的带宽。然而，该带宽取决于将任务进行卸载的用户数量。因此，我们需要先知道带宽分配情况，才能决定某个用户是否应将其任务进行卸载。为了克服这种依赖性问题，我们采用了一种分支启发式方法。其核心思想是：对于任意接入点m，能够卸载其任务的用户数量存在一个上界和下界。下界对应于具有静态卸载决策任务的用户数量，而上界则对应于关联到接入点m的最大用户数量Nm。

定义5.1。 接入点 m 的卸载容量 定义为 MEC环境 中已接受并执行的任务数量。我们将其记为 πm，其表达式如下：

$$ \pi_m = \sum_{n}^{Nm} \sum_{k} x_{um,n,k} $$

解决子问题的策略非常简单：即找到使卸载成本最小的最优πm。我们将约束C9 添加到子问题（12）中：

C9: $$ \sum_{n}^{Nm} \sum_{k} x_{um,n,k} = \pi_m $$ (13)

为了实现良好且快速的卸载决策，本地卸载管理器使用贪心启发式方法来求解子问题（12）。贪心最优云小站优先选择启发式（GBC‐SFH）提供了一种启发式方法，用于确定哪些用户进行卸载、需卸载的计算量以及为每个卸载任务选择执行的云小站。GBC‐SFH 按递增顺序遍历所有可能的卸载容量值 πm，如算法 1 所示。简而言之，该方法的核心思想是在第一步中通过在约束条件C1− C4 和 C6− C8 下最小化拉格朗日成本 Ze um,n,k+ λkck，为所有静态卸载任务找到最优云小站选择。因此，每个静态卸载任务都将被卸载到使拉格朗日成本最小的云小站上。

对于每个动态卸载决策任务，GBC‐SFH 试图选择最优云小站并计算需卸载的计算量的最佳比例aum,n。根据资源可用性，GBC‐SFH 可以将任务卸载或由用户设备本地执行aum, n = 0。由于接入点的无线带宽可能不足以卸载所有动态卸载决策任务，我们需要定义一个顺序来确定哪些动态卸载决策任务优先进行卸载。为此，我们根据以下公式为每个任务定义卸载优先级：

$$ \xi_{um,n} = Z^l_{um,n} - \min_{k \in K} (Z^e_{um,n,k}); \text{ under } a_{um,n} = 1 $$

此处，卸载优先级定义为本地成本减去所有计算量均卸载至最优云小站时的成本。其思想是，当ξ u m,n越大时，用户um, n越倾向于将其任务进行卸载。与静态卸载决策任务不同，在动态卸载决策任务中，我们需要计算需卸载的计算量（aum ,n）。为此，GBC‐SFH采用两步法。第一步，选择用于卸载用户um, n计算任务的最优云小站。在此步骤中，GBC‐SFH选择使拉格朗日成本 Ze u m,n ,k+ λ k c k 最小的云小站约束C1 − C4、C6 −C7 和aum,n= 1。在选择最优云小站后，GBC‐SFH 为当前用户计算aum, n 的最优值。该最优值aum,n 是以下问题的解：

min(Ze um,n, k+ Z l um,n)
Subject to: constraint C7. (14) 公式（14）是一个仅含一个变量的简单问题，其最优解可通过导数符号规则求得[28]。定理5.2表明了该问题最小值的取得条件。

定理5.2。 设ψum,n 和 μum,n 分别为动态卸载决策任务的上传数据-计算比率以及用户um, n 的本地-远程卸载成本比率。它们定义如下：

$$ \psi_{um,n} = \frac{up_{um,n}}{\gamma_{um,n}} $$

$$ \mu_{um,n} = \frac{w_{um,n} \cdot [\kappa \cdot f^3_{um,n} \cdot c_k \cdot \beta_{um,n} + (1 - \beta_{um,n}) \cdot (c_k - f_{um,n}) - \beta_{um,n} \cdot P^{idle} {um,n} \cdot f {um,n}]}{c_k \cdot f_{um,n} \cdot (P^{tx/rx} {um,n} \cdot \beta {um,n} + 1 - \beta_{um,n})} $$

当满足以下条件时，公式(14)取得最小值：

• a用户第m个AP，第n个用户 = 1，当且仅当：
  $$ \psi_{um,n} < \mu_{um,n} $$

• a用户第m个AP，第n个用户 = 0，当且仅当：
  $$ \psi_{um,n} > \mu_{um,n} $$

• 问题为常数，当且仅当：
  $$ \psi_{um,n} = \mu_{um,n} $$

证明。 定理5.2的证明详见附录。

根据定理5.2，动态卸载决策任务存在三种可能的情况：（1）当aum,n = 1时，整个计算必须被卸载；（2）当aum,n = 0时，不进行任何卸载；（3）当方程（14）为常数时，aum,n的所有可能取值

均具有相同的性能表现。由于计算卸载旨在提升性能，在此情况下我们选择不进行卸载，即设置aum,n = 0。一旦卸载任务数量达到当前卸载容量（πm），剩余的任务将由用户设备本地执行。

因此，在最坏情况下，当没有静态卸载决策任务时，GBC‐SFH在外层循环中迭代Nm次，这意味着对任务进行排序的复杂度为Nm · log(Nm)，在内层循环中分配任务的复杂度为Nm ·K。因此，最大总迭代次数为N²m ·K+N²m · log(Nm)。因此，GBC‐SFH的复杂度为 O(N²m · log(Nm))，特别是当每个接入点关联的用户数量较小时，该算法速度很快 14, 21, 33 。

5.2 多接入边缘计算计算卸载管理器

拉格朗日对偶问题的外层是主问题。它确保原始方程（9）具有可行的计算卸载解。求解拉格朗日对偶问题的最优解需要对所有解空间和拉格朗日乘子值进行穷举搜索，这通常是一项困难的任务[9]。因此，我们需要采用一种更快的方法。在本研究中，我们使用基于次梯度的启发式方法[31]。所提出的启发式方法由MEC计算卸载管理器MEC计算卸载管理器使用，包含三个步骤，如算法2所示。首先，它求解子问题

算法1：本地卸载管理器：GBC-SFH
输入：
1: Πm: 卸载容量的集合；
输出： 输出卸载决策 X、比率 A 和成本 Z；
2: 将 Πm按升序排序；
3: 对于 πm ∈ Πm, do
4: 分配带宽使用公式(1)；
5: 将每个静态卸载决策任务卸载到使 Ze u最小的云小站k m,n,克 + λkck在约束条件C1 −C4 和 C6 − C8下；
6: nboffloaded_task=静态卸载决策任务的数量；
7: 计算 ξu m,n针对每个动态卸载决策任务；
8: 将动态卸载决策任务按 ξ nm的降序排列；
9: 当nboffloaded_task ≤ πm,时执行循环
10: 选择使 Ze u最小的云小站k m,n,克 + λkck在约束 C1 − C4、C6 −C7 下和au m,n= 1;
11: 计算au的最优值 m,n使用定理5.2；
12: if aum,n== 0, then
13: 没有卸载。该动态卸任务必须在本地执行；
14: else
15: 将此动态卸载任务卸载到云小站k；
16: nboffloaded_task++;
17: 结束 if
18: 如果 (没有更多任务) 且 (nboffloaded_task< πm)，则
19: 跳出 while 循环。对于该 πm值，不存在可行解；
20: 结束 if
21: 结束 while
22: 所有剩余的任务必须在本地执行；
23: 更新最佳卸载成本 Z、比率 A 和决策 X；
24: 结束循环

由GBC‐SFH在本地卸载管理器中针对当前的拉格朗日乘子 λ进行处理。接着，MEC计算卸载管理器检查所获得的卸载方案是否不可行。如果是，则使用拉格朗日调整启发式 (LAH)通过局部搜索获得一个可行解。LAH启发式方法的思想是检查每个云小站是否满足约束C5。当某个云小站不满足该约束时，LAH启发式方法会将从该云小站卸载的部分任务重新分配给另一个满足所有约束的云小站。

最后，MEC计算卸载管理器通过以下公式更新拉格朗日乘子：

$$ \lambda_k(t+ 1)= \lambda_k(t)+ \theta(t) \cdot \left( \sum_{m} \left( \sum_{n} x_{um,n,k} \cdot c_k \right) - F_k \right) $$ (15)

其中 θ(t)是更新步长。在本研究中，我们使用Held和Karp公式[9, 31]来按如下方式更新此步长：

$$ \theta(t)= \eta(t) \cdot \frac{Z^* -Z(t)}{\sum_{k=1}^{K} \left( \sum_{m} \sum_{n} x_{um,n,k} \cdot c_k - F_k \right)^2} $$ (16)

其中 η(t)是一个递减自适应参数 0< η(0) ≤ 2, Z∗是方程(9)得到的最佳解，而 Z(t)表示拉格朗日对偶问题的当前解。 η(t)可由以下公式表示：

$$ \eta(t+ 1)= \begin{cases}
\vartheta \cdot \eta(t) & \text{if } Z(t) \text{ did not increase} \
\eta(t) & \text{otherwise}
\end{cases} $$ (17)

如文献[9, 31],所建议，我们设定 ϑ= 0.9 和 η(0)= 2。主问题重复这些步骤直到满足停止条件，即最大迭代次数Itmax和更新步长的最大容忍误差 ε(θ ≤ ε)。

算法 2: MEC计算卸载管理器
输入：
1: Itmax：最大迭代次数；
2: ε：一个无穷小数；
输出： 所有用户的卸载决策和云朵选择；
3: 随机初始化 λk；
4: Zmax= −∞；
5: 当 (t < Itmax 且 θ(t) > ε) 时，执行以下操作：
6: 对于 (m ∈ M)，执行以下操作：
7: Zm(t)=从本地卸载管理器m获取子问题m的解；
8: 结束循环；
9: Z(t) =∑m∈M Z(t)m −∑k ∈K λk · Fk；
10: 如果 (Z(t) > Zmax)，则：
11: Zf easible=使用启发式LAH寻找一个可行解；
12: 如果 (Zf easible< Z ∗)，则：
13: Z∗= Zf easible；
14: 更新原始问题的最佳解；
15: 结束条件；
16: Zmax= Z(t)；
17: 结束条件；
18: 使用公式(15)、(16)和(17)更新拉格朗日乘子和 η；
19: 结束循环

6 数值结果

在本节中，我们使用真实系统配置的特性来评估DM2‐ECOP的性能。我们采用一个由城区构成的MEC环境，该环境包含20个形成环形拓扑的接入点。任意两个接入点之间的延迟为 3ms，每个接入点与远程云之间的延迟为100ms[14, 33]。假设四个云小站在网络中等距部署，即云粒1与AP 1共址，云粒2与AP 6共址，云粒3与AP 11共址，云粒4与AP 16共址。为了研究我们的卸载策略的性能，我们考虑了四种边缘云配置。表2列出了测试中所考虑的云小站配置列表。我们采用了公共云提供商（如亚马逊网络服务（AWS）和微软Azure）使用的实际配置，以模拟DM2‐ECOP策略在现实场景中的行为。

每个接入点的无线带宽为150兆比特每秒。分配给每个用户的带宽是使用Bianchi模型中的参数设置估算的[1]。类似于参考文献[33],我们

表2. 用于测试的云粒配置列表

配置	计算能力 Fk 和分配 ck，单位为千兆CPU周期/秒
	云粒1
	c1
配置1	10
配置2	15
配置3	10
配置4	15

表3. 我们测试所用真实应用程序的特征

应用程序	γum,n (千兆CPU周期)	upum,n (千字节)	dwum,n (字节)	tum,n (秒)	类别
FACE	12.3	62	60	5	静态卸载决策任务
语音	15	243	50	5.1	静态卸载决策任务
对象	44.6	73	50	13	静态卸载决策任务
Linpack	50	10,240	120	62.5	动态卸载决策任务
CPUBENCH	3.36	80	80	4.21	动态卸载决策任务
PI BENCH	130	10,240	200	163	动态卸载决策任务

假设每个接入点连接的用户数量Nm不超过20。具体而言，Nm取值自{5, 10, 15, 20}。每个用户运行表3中的一个应用程序。前三个应用程序是静态卸载决策任务；其余为动态卸载决策任务[11]。我们假设P tx/rx um 、n = 10 ∗P idle um和nP idle um分别为n = 100mW，如参考文献[3]所示。每个用户的本地计算能力从fum、n ∈[0.8, 1, 1.2]千兆周期中随机选取。

将DM2‐ECOP的性能与文献中的两种卸载策略进行比较：

• 最近云点卸载 (NCO)[14, 33] ：在这种策略中，每个接入点都与最近的云点相关联。因此，连接到该接入点的所有用户都将任务卸载到同一个云点。当某个云点过载时，任务将被迁移到另一个云点。
• 完全云卸载 (FCO)[4, 5] ：在这种情况下，用户将任务卸载到远程云。为了合理比较卸载策略DM2‐ECOP、NCO和FCO的性能，我们假设在远程云中为每个卸载任务分配的计算能力为10吉周期。

下文中，默认的云小站配置为第一种配置（配置1），且每个接入点处的用户密度视为相同，即每个接入点的用户数量相同。此外，MEC计算卸载管理器针对DM2‐ECOP的停止准则为It max = 100作为最大迭代次数， ε= 10⁻²⁰作为更新步长的最大容忍误差。

6.1 DM2‐ECOP的收敛性

为了评估DM2‐ECOP的性能及其收敛到可行解的情况，表4展示了获得可行解所需的迭代次数以及更新步长的最终值（θ）。正如预期，随着用户数量的增加，所需迭代次数也随之增加

表4. DM2‐ECOP 收敛到可行解所需的迭代次数和更新步长

用户数量	迭代次数	更新步长 θ
100	15	0.0
200	20	9.12 × 10⁻²²
300	29	5.09 × 10⁻²¹
400	43	4.46 × 10⁻²¹

随着网络的扩展，更新步长在少量迭代后收敛到最大容忍误差 ε；而当用户数量增加时，这种收敛性会发生变化。得益于我们工作中采用的Held和Karp公式来更新拉格朗日更新步长，DM2‐ECOP卸载策略实现了快速收敛。

6.2 卸载性能比较

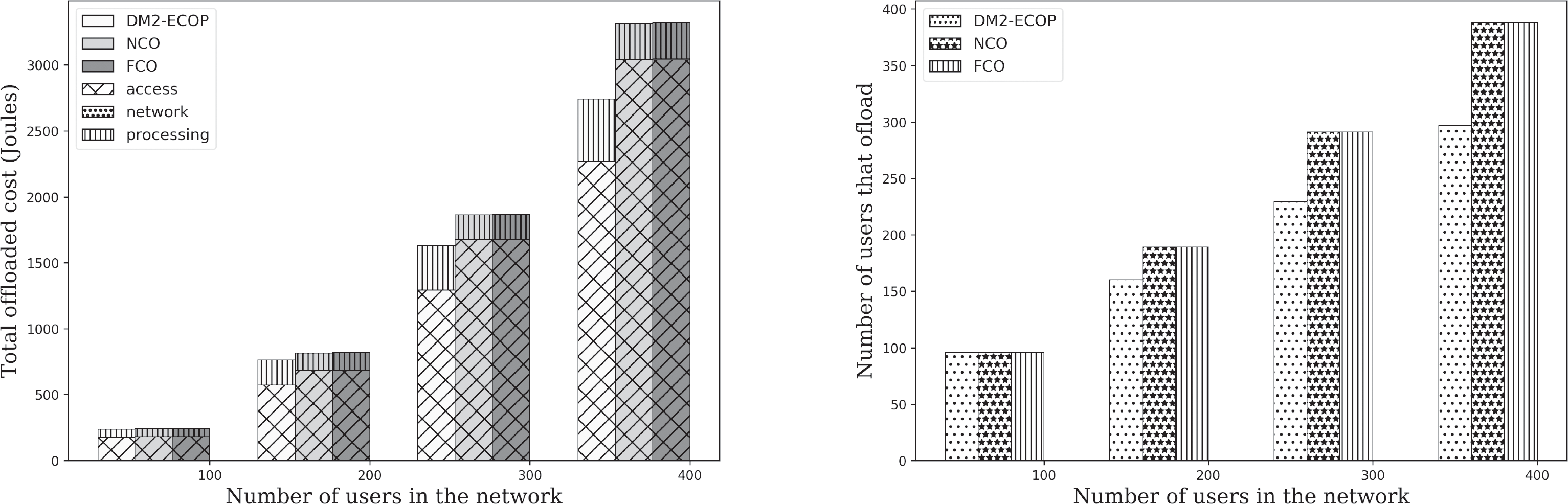
图5绘制了在设置成本参数 β= 1时，DM2‐ECOP、NCO和FCO 的卸载性能。我们还区分了与网络接入、网络回传和处理相关的成本。我们注意到，与NCO和FCO相比，DM2-ECOP降低了总卸载成本。更准确地说，我们可以看到DM2-ECOP的接入成本最低，但处理成本最高。这是由于DM2-ECOP使用的带宽分配启发式方法，该方法通过最小化每个AP的卸载容量（π），试图最大化分配给每个用户的带宽。因此，与NCO和FCO相比，使用DM2‐ECOP能够将任务卸载到MEC的用户较少。然而，当无线带宽足以卸载所有任务时，DM2‐ECOP与NCO是等效的，如表4所示，其中网络中有100名用户。

为了理解用户密度对卸载性能的影响，我们在图6中研究了在不同用户密度下 DM2‐ECOP相较于NCO的卸载增益。我们考虑了四种场景，其中拓扑结构被划分为两个区域，每个区域包含10个接入点。在场景1中，两个区域的用户密度相同。在场景2中，区域1的用户密度是区域2的两倍。在场景3中，区域1的用户密度是区域2的三倍。最后，在场景4中，区域1的用户密度是区域2的四倍。在图6中，我们注意到，当用户密度升高时，DM2‐ECOP相较于NCO的卸载增益也随之上升。例如，当网络中有200个用户时，场景1的增益为6.1%，而场景4的增益为10.5%。这是因为在NCO中的云朵选择是静态的，因此该策略需要在云小站过载时迁移部分任务。从而导致额外的卸载

开销。然而，DM2‐ECOP在卸载决策时会根据系统和网络资源的可用性动态地寻找最优云小站选择。

6.3 成本参数 β 对卸载性能的影响

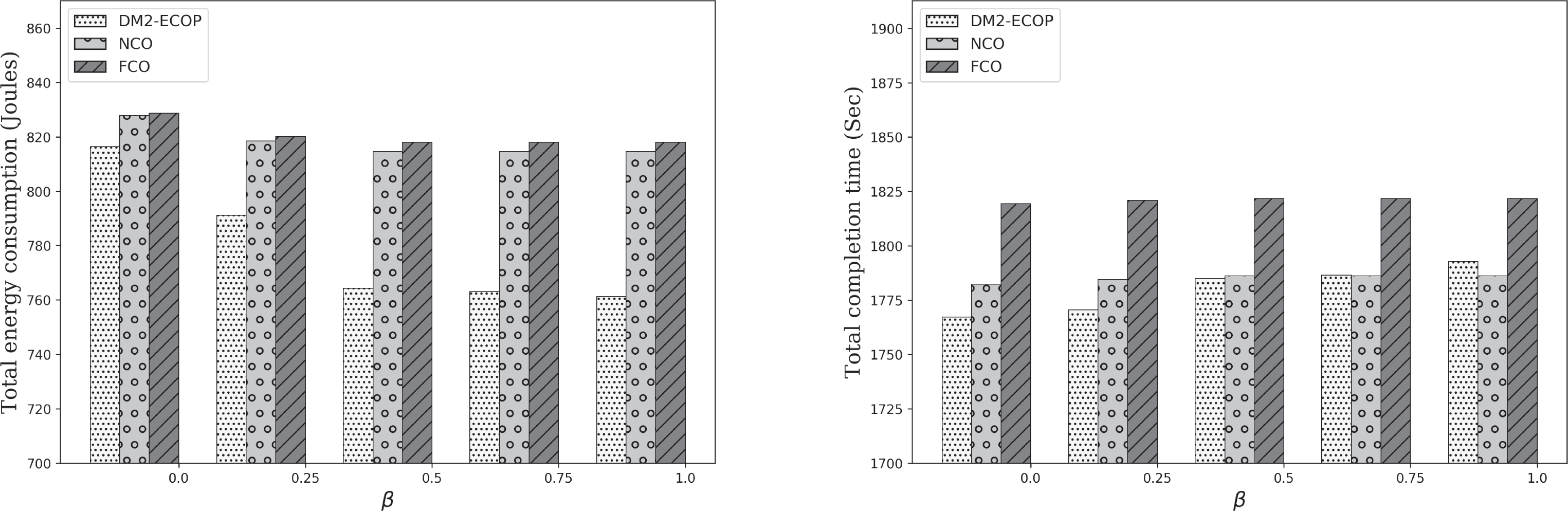
图7研究了卸载成本参数 β对DM2‐ECOP、NCO和FCO策略性能的影响。如图7(a) 所示，DM2‐ECOP 的能耗在所有可能的 β取值下均优于NCO和FCO。事实上，即使我们将 β 设为0，即完全优先考虑任务的完成时间，DM2‐ECOP 仍能获得更优的性能。此外，当我们增加 β的值时，所获得的性能更佳。因此，无论卸载成本是能耗、完成时间，还是能耗与时间的组合，DM2‐ECOP 在能耗方面均表现出更优的性能。这归因于 DM2‐ECOP中采用的动态云点选择。

在图7（b）中，我们研究了 β对完成时间性能的影响。我们注意到，DM2‐ECOP和NCO的完成时间优于FCO，因为云小站

靠近用户。此外，DM2‐ECOP的完成时间最低，其中 β= 0。然而，当 β接近1时，NCO 的完成时间优于DM2‐ECOP。因此，NCO在完成时间方面性能最佳。事实上，当 β接近1 时，能耗在卸载成本表达式中比完成时间更为重要。DM2‐ECOP通过将较少的任务卸载到多接入边缘计算（MEC）来降低卸载成本，如图5所示，以最小化无线接入层的能耗。结果，更多任务在本地执行，导致完成时间增加。

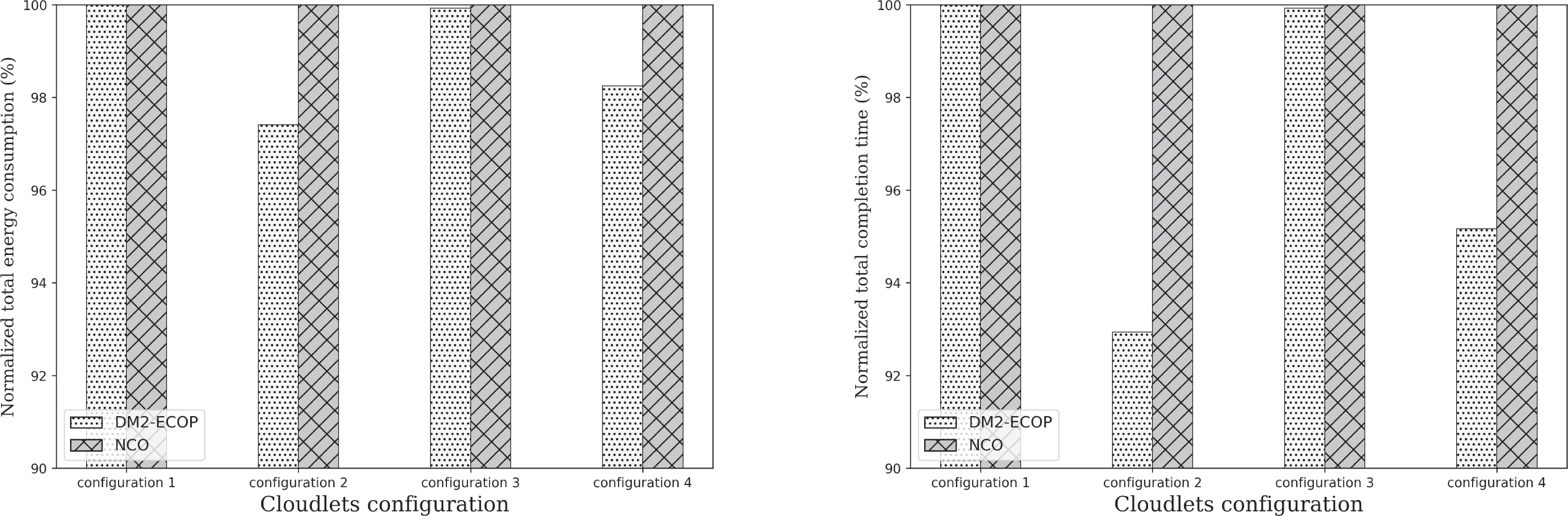
6.4 云小站配置的影响

接下来，我们研究卸载策略在异构边缘云配置下的性能表现。在图8中，我们考察了卸载策略DM2‐ECOP和NCO在本节开头提出的四种边缘云配置下的性能表现。我们观察到，当云小站的配置完全相同时（例如配置1），DM2‐ECOP与NCO的性能相当。然而，在为每个任务分配的计算资源具有异构性的情况下（这对应于更真实的应用场景），DM2‐ECOP在能耗和完成时间方面表现出更优的性能。这可以解释为：DM2‐ECOP会将任务卸载到最优的云小站，而NCO则将任务卸载到最近的云小站。我们还可以注意到，即使两种配置中为每个任务分配的资源相同，DM2‐ECOP在配置2下的性能仍优于配置4。这是因为在配置4 中，总计算能力是异构的，因此NCO需要将部分任务从边缘云1和2迁移到边缘云3和4。综上所述，这些结果表明，DM2‐ECOP在不同的边缘云配置下均能实现良好的卸载性能。

6.5 应用特性的影响

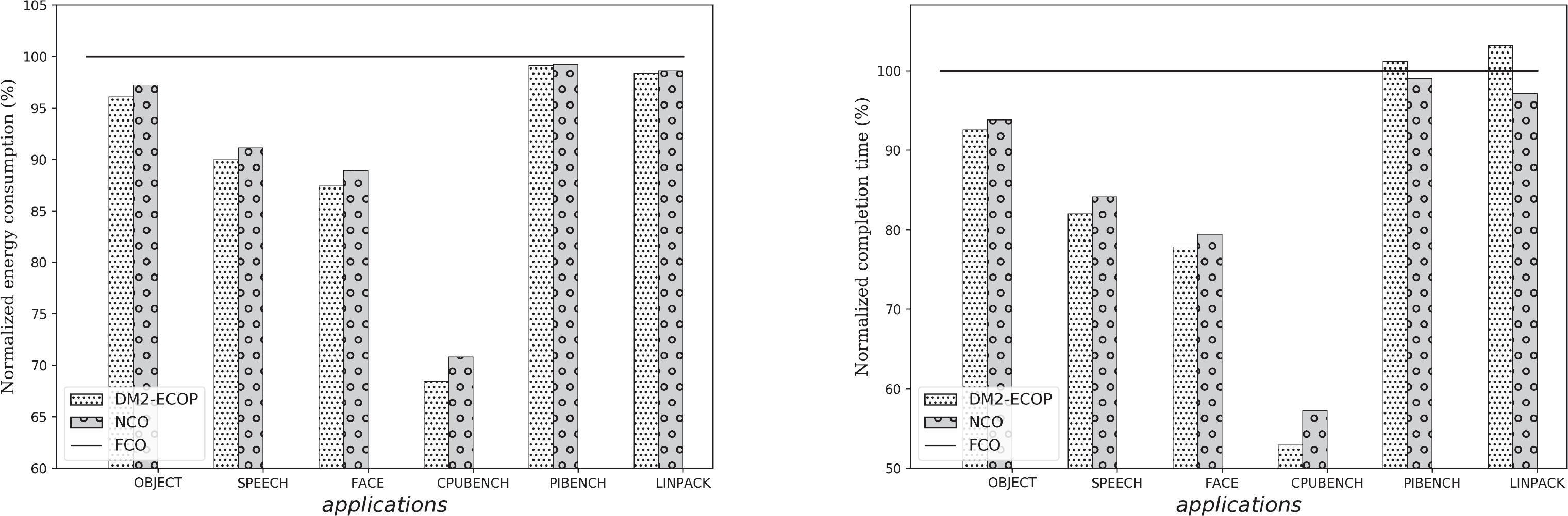
如我们之前的分析模型所示，应用程序的特性在卸载性能的效率中起着关键作用。为了理解这一作用，我们研究了应用程序对卸载成本和卸载计算量的影响，aum ,n。

图9展示了在云朵配置3下，各种卸载策略针对每个应用程序的性能表现。我们注意到，对于静态卸载决策任务，DM2‐ECOP在能耗和完成时间方面优于NCO。实际上，静态卸载决策任务必须被卸载，而DM2‐ECOP在决策时会尝试找到最优的云朵选择

时间。然而，FCO 卸载到最近的云点，这会引发额外的卸载成本，因为某些任务必须迁移 到其他云小站。但对于动态卸载决策任务，我们注意到，在应用程序无需向云小站上传大量数据的情况下（例如CPUBENCH），DM2‐ECOP 的能耗和完成时间最低。然而，当应用程序需要处理大量数据时（如Linpack和PIBENCH），NCO 和FCO 的完成时间优于DM2‐ECOP。这是因为DM2‐ECOP 在向云小站上传大量数据时，会尽量在本地执行应用程序，以最小化用户的接入成本。

最后，为了深入分析DM2‐ECOP在动态卸载决策任务下的性能，我们研究了用户数量以及远程与本地处理能力之比对卸载决策的影响。在图10(a)中，我们绘制了每个接入点的用户数量以及因此分配给每个用户的带宽对卸载决策的影响。红色区域对应仅在本地执行任务的情况（即，aum ,n = 0），绿色区域对应任务完全被卸载的情况（即，aum ,n = 1）。除了卸载决策外，我们还绘制了三个动态卸载决策任务（即Linpack、CPUBENCH和PI BENCH）的上传数据‐计算比率ψ u m,n。如图所示，

当增加每个接入点的用户数量时，这三种应用程序的表现并不相同。事实上，Linpack 是最敏感的应用程序，当用户数量超过14 时便停止卸载。然而，CPUBENCH 是最不敏感的应用程序，因为它直到用户数量达到37 时才停止卸载。这是由于Linpack 在卸载时传输的数据量远大于CPUBENCH。在图10(b)中，我们研究了本地处理能力与远程处理能力之比对卸载决策的影响。与图10(a)类似，我们也绘制了Linpack、CPUBENCH 和PI BENCH 的上传数据‐计算比率ψum，n。我们可以看到，当远程处理能力与本地处理能力的比值增大时，我们的方案倾向于更多地卸载任务。然而，与图10(a)不同的是，Linpack 对该比值的增加相比CPUBENCH 和PI BENCH 更不敏感。事实上，由于Linpack 需要卸载的总数据量较大，只有当远程处理能力相对于本地处理能力非常强时，卸载才变得有利。

7 结论

在多用户、多云朵移动边缘计算环境中，计算卸载是一个具有挑战性的问题。本文提出了一种新的计算卸载策略，以决定哪些用户应进行卸载以及卸载到哪个云小站。首先，我们将该问题建模为一个非线性混合二进制整数规划问题。然后，我们提出一种高效的分布式启发式算法，采用拉格朗日分解方法求解该问题。所提出的启发式方法利用分支算法来最大化带宽分配并最小化卸载成本。

此外，与其他研究相比，我们的方案（DM2‐ECOP）考虑了两类可卸载任务：必须在远程执行的静态卸载决策任务，以及可在本地和远程执行的动态卸载决策任务。我们还为静态和动态决策任务引入了卸载计算比例，该比例表示应用程序在终端本地执行的部分以及应卸载到云小站的部分。

所获得的数值结果表明，在不同场景和边缘云配置下，与现有的卸载策略相比，卸载成本方面性能有所提升。此外，由于我们假设所有任务具有相同的优先级，并且在云小站上不共享资源（同一CPU），我们证明了卸载计算比例的最佳值要么为0，要么为1。

在未来的工作中，我们将考虑一种自适应卸载策略，其中被卸载的任务必须在运行时确定。此外，在本文中，我们假设每个移动设备一次仅执行一个任务。在未来的工作中，我们计划探索应用程序由任务依赖图表征的情况。在这种情况下，可以同时将多个任务卸载到远程云小站或云。