PCA主成分分析

概述：

消除可能存在相关性的特征，数据降维至无相关性的特征，即提取主成分，比如原来有M维特征，降维为N为特征，不是单纯的舍弃某些特征，而是通过映射矩阵进行映射
协方差表示两个随机向量之间的线性相关性
协方差矩阵表示一组随机向量之间的两两线性相关性

步骤：

比如有5个样本，每个样本有6个特征X1，X2，…X6,将其降为3维

1 对每个特征求均值，并求取均值之后的矩阵（5*6）

2 求协方差矩阵（6 * 6）

两个向量（特征）之间的协方差，此处均值为0

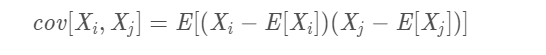
6 * 6的协方差矩阵则为

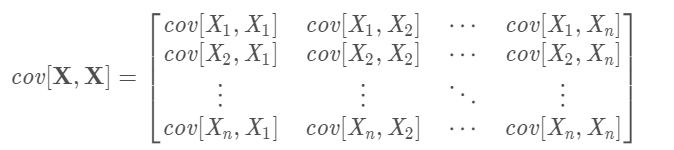
3 求协方差矩阵的特征值和特征向量

由最大的三个特征值对应的特征向量构成投影矩阵！比如前三个特征值之和（？）已经达到95%，即把它降成3维之后仍保留95%的信息，所以选择降维之后的维数为3

4 由投影矩阵求出降维后的特征矩阵

补充

不影响标签！每一行为样本，每一列是特征维度，比如每个样本有4个特征，对应一个标签，现在有150个样本，对应150个标签，A为150*4的矩阵，$1/4A^{T}A$为$4\ast 4$为协方差矩阵（$1/4$可有可无吧，不影响特征值和特征向量），求该矩阵最大的几个（比如$2$）的特征值对应的特征向量组成的映射矩阵（$4\ast 2$），每个样本之前的特征为$1\ast 4$，现在为$1\ast 4\ast 4\ast 2=1\ast 2$
，即降低了数据的维度。
我今天是想到样本不平衡（比如正负样本数量悬殊）时想到这个问题，现在想通了，PCA解决不了样本不平衡的问题，只能降低样本的维度，标签还是标签。