集成学习之GBDT

1.预备知识

集成学习之GBDT预备知识

2.提升树

被认为是统计学习中性能最好的方法之一

2.1 一般步骤

2.1.1 模型

使用的也是加法模型：$$f_M(x)=\sum _{m=1}^{M}T(x;{\Theta }_m)$$，其中$M$为树的个数，$T(x;{\Theta }_m)$表示决策树，${\Theta }_m$为决策树的参数。

2.1.2 损失函数

• 回归问题：平方误差损失函数
• 分类问题：
  • 二分类问题：指数损失函数
  • 多分类问题：softmax
  • 一般决策问题：自定义损失函数

2.1.3 优化方法

前向分步算法：

如书上：
其中当前模型$f_m(x)$已知。

2.2 二分类问题的提升树

2.2.1 基学习器

CART决策树

2.2.2 损失函数

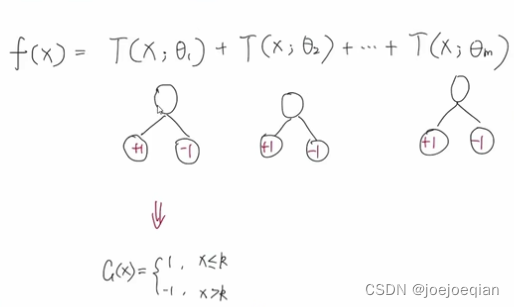
使用指数损失函数：$$\begin{gathered} f(x)=\sum _{m=1}^M{\beta }_{m}b(x;{\gamma }_m) \\ {f}_M(x)=\sum _{m=1}^{M}T(x;{\Theta }_m) \end{gathered}$$

2.2.3 说明

提升树相当于Adaboost算法的特殊情况，

Adaboost的模型为：$$\begin{array}{rl}f(x)& =\sum _{m=1}^M{\alpha }_m{G}_m(x)\\ & ={\alpha }_1{G}_1(x)+\cdots +{\alpha }_m{G}_m(x)+\cdots +{\alpha }_M{G}_M(x)\end{array}$$，其中${\alpha }_m$由$G_m(x)$的"分类误差率"决定，训练样本$G_m(x)$：提高前一轮“错误分类”的样本的权值，降低前一轮“正确分类”的样本的权值。

它只是将：

• 1.基分类器G(x)限制为二分类树；
• 2.基分类器权重${\alpha }_m$全部置为1。
  如图：
  

2.2.4 原理

只要我们使用的是指数损失函数，就可以用指数损失函数来调整样本数据的权重，从而让每个基分类器学到不同的内容。

指数损失函数：
$$L(y,f(x))=\exp [-yf(x)]$$
，其中当$f(x)$分类正确时，与$y$同号，$L(y,f(x))<=1$。当$f(x)$分类错误时，与$y$异号，$L(y,f(x))>1$。

2.3 回归问题的提升树

2.3.1 基学习器

CART回归树
$T(x;\Theta )={\sum }_{j=1}^J{c}_{j}I(x\in R_j)$
$f_M(x)={\sum }_{m=1}^{M}T(x;{\Theta }_m)$

2.3.2 损失函数

使用平方误差损失：$L(y,f(x))=(y-f(x){)}^2$
$$\begin{array}{rl}L(y,f(x))& =(y-f(x){)}^2\\ & =[y-f_{m-1}(x)-T(x;{\Theta }_m){]}^2\\ & =[r-T(x;{\Theta }_m){]}^2\end{array}$$
，其中$r$是残差，目标就是拟合残差$r$。

2.3.3 前向分步算法

$$\begin{array}{rl}{\hat{\theta }}_m& =\arg \underset{\theta m}{\min }\sum _{i=1}^{N}L(y^{(i)},f_{m-1}(x^{(i)})+T(x^{(i)},{\theta }_m))\\ & =\arg \underset{\theta m}{\min }\sum _{i=1}^N(r_m^{(i)}-T(x^{(i)},{\theta }_m){)}^2\end{array}$$

2.3.4 思路

1.个体学习器如何训练得到
如何改变训练数据的权值或概率分布如何改变？

用残差进行拟合，一步一步的将残差缩小。

2.如何将个体学习器组合
相加

3.目标

• 使得总体损失逐步减少
  

3.一般决策问题梯度提升树GBDT

GBDT也是迭代，使用了前向分布算法，但是弱学习器限定了只能使用CART回归树模型，同时迭代思路和Adaboost也有所不同。

GBDT的思想可以用一个通俗的例子解释，假如有个人30岁，我们首先用20岁去拟合，发现损失有10岁，这时我们用6岁去拟合剩下的损失，发现差距还有4岁，第三轮我们用3岁拟合剩下的差距，差距就只有一岁了。如果我们的迭代轮数还没有完，可以继续迭代下面，每一轮迭代，拟合的岁数误差都会减小。

从上面的例子看这个思想还是蛮简单的，但是有个问题是这个损失的拟合不好度量，损失函数各种各样，怎么找到一种通用的拟合方法呢？

3.1 要解决的问题

3.2 基学习器

回归树：

$T(x;\Theta )={\sum }_{j=1}^J{c}_{j}I(x\in R_j)$
$f_M(x)={\sum }_{m=1}^{M}T(x;{\Theta }_m)$

3.3 损失函数

找到一般的损失函数：$L(y,f(x))$

3.4 前向分步算法+梯度提升

3.4.1 核心目标

1.已知加法模型，一定会存在多个优化器，不断迭代优化；
2.我们要确保，每增加一个基学习器，都要使得总体损失越来越小，即第m步要比第m-1步的损失要小。
即：$$\begin{array}{rl}& L(y^{(i)},f_m(x^{(i)}))<L(y^{(i)},f_{m-1}(x^{(i)}))\to L(y^{(i)},f_{m-1}(x^{(i)}))-L(y^{(i)},f_m(x^{(i)}))>0\end{array}$$

3.4.2 将损失函数进行处理

处理的原因就是：往我们的核心目标上靠。

$\begin{array}{rl}& L(y^{(i)},f_m(x^{(i)}))<L(y^{(i)},f_{m-1}(x^{(i)}))\to L(y^{(i)},f_{m-1}(x^{(i)}))-L(y^{(i)},f_m(x^{(i)}))>0\end{array}$

由泰勒公式：$f(x)\approx f(x_0)+f^{{}^{\prime }}(x_0)(x-x_0)$和$L(y,f_m(x))$中只有$f_m(x)$是未知量，且$f_m(x)=f_{m-1}(x)+T(x;{\Theta }_m)$，得：

$$\begin{array}{rl}L(y,f_m(x))& \approx L(y,f_{m-1}(x))+\frac{\partial L(y,f_m(x))}{\partial f_m(x)}{|}_{f_m(x)=f_{m-1}(x)}\cdot \left(f_m(x)-f_{m-1}(x)\right)\\ & =L(y,f_{m-1}(x))+\frac{\partial L(y,f_m(x))}{\partial f_m(x)}{|}_{f_m(x)=f_{m-1}(x)}\cdot T(x;{\Theta }_m)\end{array}$$

即有：

$$\begin{array}{r}L(y,f_{m-1}(x))-L(\end{array}$$