ACM-ICPC 2018 南京赛区网络预赛

最新推荐文章于 2025-06-29 16:23:00 发布

最新推荐文章于 2025-06-29 16:23:00 发布 · 896 阅读

学习笔记or周记or赛后总结专栏收录该内容

16 篇文章

订阅专栏

这次服务器很流畅，比赛体验很棒，上次杭电那场真的是气到爆炸交了题要三个小时才知道结果

而且计蒜客就算超时了也可以看到超了多少（1000ms以上会显示1009ms）

队友这次有点迷茫，两个人卡在最后那道图论题3个小时，结果还是我转过去暴力过的，所以今天做出来的四道基本上是我一个人敲出来的。所以说个人的实力还是很重要的，我们这边的一队两个人就做出10道题排名34。。。望尘莫及啊！不过还好，我才学了一年不到，我觉得自己一直也很努力，现在的成果已经很不错了^_^

比赛心得：

考前要放松，今天我早上打了一早上的游戏，考试的时候一点都不紧张，全程在认真做题（赛前打游戏哈哈哈）

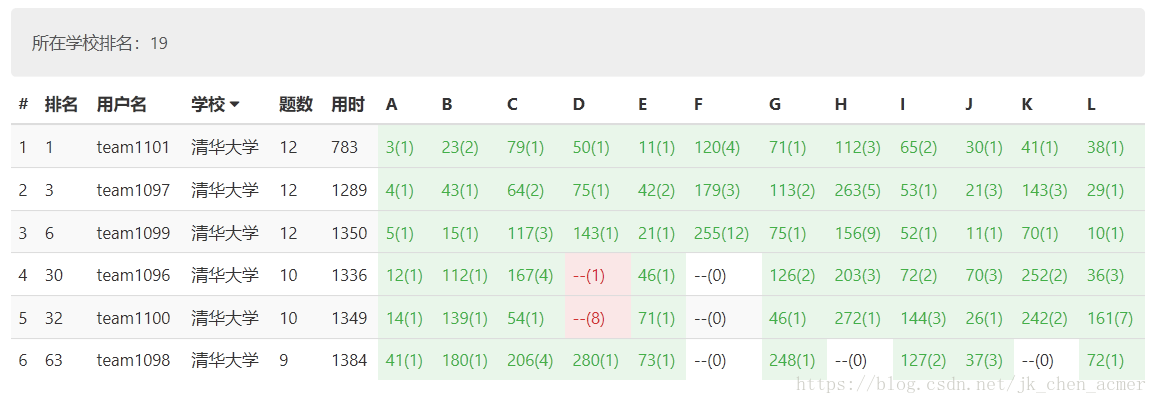
附一张清华大学的表现和我们队的表现(hh)
这里写图片描述

$\\$

A. An Olympian Math Problem

题意 :

求S%n $,S=1*1!+2*2!+...(n-1)*(n-1)!$

解析 :

水题 , $a*(a!)=(a+1)!-a!$ ,消掉后变成 $(n!-1)\%n=(k*n-1)\%n=n-1$

#include<bits/stdc++.h>
using namespace std;
#define LL long long
LL read(){
    LL ans=0;char l=' ',c=getchar();
    while(!isdigit(c))l=c,c=getchar();
    while(isdigit(c))ans=ans*10ll+c-'0',c=getchar();
    if(l=='-')ans=-ans;return ans;
}


int main(){
    int t=read();
    while(t--){
        LL n=read();
        printf("%lld\n",n-1ll);
    }
}

$\\$

E. AC Challenge

题意 :

n道题 , 每道题有值a,b和k个前提 , 前提代表你需要做完这k题才能做这题

时间t从1开始 , 每道题需要1时间来完成 , 完成后得到的价值为 $t*a+b$ , 求最大价值

解析 :

因为n的范围为20 , 所以可以状压dp , 从0状态开始bfs , 对于每个队首状态x , 枚举所有n , 如果x不包含n且满足x包含所有n所需前提 , 那么就可以转移 , 再判断一下dp值 , 如果更优则更新

#include<bits/stdc++.h>
using namespace std;
#define LL long long
#define debug(i) printf("-> %d\n",i)
LL read(){
    LL ans=0;char l=' ',c=getchar();
    while(!isdigit(c))l=c,c=getchar();
    while(isdigit(c))ans=ans*10ll+c-'0',c=getchar();
    if(l=='-')ans=-ans;return ans;
}
LL a[22],b[22];
int s[22];
LL ans[(1<<20)+9];
const LL inf=1<<60;

struct node{
    int x,ct;
    node(){}
    node(int x,int ct):x(x),ct(ct){}
};


int main(){
    int n=read();
    for(int i=0;i<=(1<<20);i++)ans[i]=-inf;
    for(int i=1;i<=n;i++){
        a[i]=read(),b[i]=read();
        int m=read();
        LL x=0;
        while(m--){
            int t=read();
            x+=(1<<(t-1));
        }
        s[i]=x;
    }

    queue<node>q;
    q.push(node(0,0));ans[0]=0;
    while(!q.empty()){
        node _=q.front();q.pop();

        int x = _.x, ct = _.ct + 1;

        for(int i=1;i<=n;i++){
            int now=(1<<(i-1));
            if(x&now){continue;}
            int tmp=(x&s[i]);//不能直接判断(x&s[i])!=s[i]
            if(tmp!=s[i]){continue;}

            int y=x+now;

            if(ans[y]<ans[x]+ct*a[i]+b[i]){
                ans[y]=ans[x]+ct*a[i]+b[i];
                q.push(node(y,ct));
            }
        }
    }
    LL A=0;
    for(int i=0;i<=(1<<20);i++)A=max(A,ans[i]);
    printf("%lld\n",A);
}

$\\$

J. Sum

题意 :

定义 : $a若合法 , 不存在i^2|a \;,\; f(n)表示将n写成a*b的方案数(a,b合法,1*2\not=2*1,2*2=2*2)$

每组案例输入n求 $f(1)+f(2)+...f(n)$

解析 :

因为n范围2e7 , 所以不可能以n为中心做 , 那么把a和b作为中心

首先预处理每个数的合法性( 线性筛,一个合法的数遇到它的第一个质因子相乘变成不合法 , 一个不合法的数乘任何素数也是不合法 )
做一下合法性的前缀和 $sum[]$
遍历 $i:1\to n$ , 对于每个 i , 将其当成a , 那么b (小于等于a) 的范围为 $[1,n/a]$ , 那么a对于答案的贡献就是 $sum[n/a]$

结果每次遍历1~n为a判断是否合法TLE了！线性筛+O(n)TLE了真的是无语了

然后我把合法的数放进一个数组里面就过了 , 好像2e7里面有1.2e7个合法的数。。。

#include<bits/stdc++.h>
using namespace std;
#define LL long long
LL read(){
    LL ans=0;char l=' ',c=getchar();
    while(!isdigit(c))l=c,c=getchar();
    while(isdigit(c))ans=ans*10ll+c-'0',c=getchar();
    if(l=='-')ans=-ans;return ans;
}

const int maxn=2e7+5;
LL sum[maxn];

bool nprime[maxn];
int prime[maxn>>1],cnt;
bool vis[maxn];


int A[15000000],ww;
void init()
{
    cnt=0;
    for(int i=2;i<=maxn-5;i++)
    {
        if(!nprime[i])
        {
            prime[++cnt]=i;
        }
        if(vis[i])
        {
            for(int j=1;j<=cnt&&prime[j]*i<=maxn-5;j++)
            {
                nprime[prime[j]*i]=1;
                vis[prime[j]*i]=1;
                if(i%prime[j]==0) break;
            }
        }
        else
        {
            for(int j=1;j<=cnt&&prime[j]*i<=maxn-5;j++)
            {
                nprime[prime[j]*i]=1;
                if(i%prime[j]==0) {
                    vis[prime[j]*i]=1;
                    break;
                }
            }
        }
    }
    sum[0]=0;ww=0;
    for(int i=1;i<=maxn-5;i++){
        if(!vis[i])A[++ww]=i;
        sum[i]=sum[i-1];
        if(!vis[i])sum[i]++;
    }
}
int main(){
    init();
    int t=read();
    while(t--){
        int n=read();
        LL ans=0;
        for(int i=1;i<=ww&&A[i]<=n;i++){
            int en=n/A[i];
            ans+=sum[en];
        }
        printf("%lld\n",ans);
    }
}

$\\$

L. Magical Girl Haze

题意 :

求1到n的最短路径 , 你可以把其中k条边的距离变成0

解析 :

好像是某个算法的裸题 , 我是直接暴力bfs过的 , 也才100多ms

每个点有k种状态 , 分别开vis数组 , 也就是1个点可能会被走k次 , dp[i][j]表示走到i点花费j次变化的最短路径

有两个比较大的剪枝 1. 因为是走到n便更新一次ans , 所以bfs到一个点的时候可以和ans比较 , 如果已经大于等于ans了说明不能比ans更优了 , 就可以直接continue了 . 2. 判断是否比当前dp更优不只是比较dp[pos][ct] , 还要比较dp[pos][小于ct] , 因为如果花了比ct还少的变化都更优 , 说明当前不优秀

#include<bits/stdc++.h>
using namespace std;
#define LL long long
#define debug(i) printf("-> %d\n",i)
LL read(){
    LL ans=0;char l=' ',c=getchar();
    while(!isdigit(c))l=c,c=getchar();
    while(isdigit(c))ans=ans*10ll+c-'0',c=getchar();
    if(l=='-')ans=-ans;return ans;
}

const int N=200009;
const LL inf=(1ll<<62);

int head[N],nex[N],to[N],now;LL v[N];
void add(int a,int b,LL vv){
    to[++now]=b,v[now]=vv,nex[now]=head[a],head[a]=now;
}

LL dp[N/2][12];

struct node{
    int p,ct;LL val;
    node(int p,int ct,LL val):p(p),ct(ct),val(val) {}
};

bool judge(LL val,int p,int ct){
    for(int i=0;i<=ct;i++){
        if(dp[p][i]<=val)return false;
    }
    return true;
}

int main(){
    int t=read();
    while(t--){
        now=0;memset(head,-1,sizeof(head));
        int n=read(),m=read(),k=read();
        for(int i=1;i<=n;i++){
            for(int j=0;j<=k;j++){
                dp[i][j]=inf;
            }
        }
        for(int i=1;i<=m;i++){
            int a=read(),b=read();LL v=read();
            add(a,b,v);
        }
        queue<node>q;

        LL A=inf;

        q.push(node(1,0,0));dp[1][0]=0;
        while(!q.empty()){
            node _=q.front();q.pop();
            int p=_.p,ct=_.ct;LL va=_.val;
            if(va!=dp[p][ct]||va>=A)continue;

            for(int i=head[p];~i;i=nex[i]){
                int u=to[i];

                if(u==n){
                    if(ct<k)A=min(A,dp[p][ct]);
                    else A=min(A,dp[p][ct]+v[i]);
                    continue;
                }

                if(ct<k){
                    int st=ct+1;
                    LL val=dp[p][ct];
                    if(judge(val,u,ct+1)){
                        dp[u][ct+1]=val;
                        q.push(node(u,ct+1,val));
                    }
                }
                int st=ct+1;
                LL val=dp[p][ct]+v[i];
                if(judge(val,u,ct)){
                    dp[u][ct]=val;
                    q.push(node(u,ct,val));
                }
            }
        }

        printf("%lld\n",A);
    }
}