偏序全序与拓扑排序-优快云博客

偏序与全序

这个应该是离散数学的内容，这里用口语来描述一下

偏序：两点之间不存在环路，不要求连通与否。

例子：合成需要药水A，药水B，这是两条连通的路，不存在环路，但是没有规定药水A和药水B的关系。
全序：就是在偏序的基础之上，有向无环图中的任意一对顶点还需要有明确的关系

比如药水A需要在药水B之前使用，就使这3个物品两两相连了。

拓扑排序

在图论中，由一个 有向无环图（DAG）的顶点 组成的序列，当且仅当满足下列条件时，称为该图的一个拓扑排序（Topological sorting）。

（1）每个顶点出现且只出现一次 -> 图中 无两个相同 的地点
（2）若A在序列中排在B的前面，则在图中不存在从B到A的路径。-> 在图中只存在 序列位后 通往 序列位前 的路

此拓扑排序的思想是：

从有向图中选取一个没有前驱的顶点，并输出之；
从有向图中删去此顶点以及所有以它为尾的弧；

重复上述两步，直至图空或者找不到无前驱的顶点为止。

看例子：
这里写图片描述
输出排序结果：v6-v1-v4-v3-v2-v5

作用：

检验一个图有没有环->判断关系是否矛盾
求关键路径->求事件执行顺序or比赛排名

代码：

#include<iostream>
#include<string.h>
#include<algorithm>
#include<vector>
#include<stdio.h>
#include<queue>
#include<set>
#define N 509
using namespace std;

int in_degree[N];
bool M[N][N];
bool vis[N];
int ans[N],now;
int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    while(m--){
        int a,b;scanf("%d%d",&a,&b);
        if(!M[a][b])in_degree[b]++;//考虑到重边的问题
        M[a][b]=1;
    }
    while(1){
        int hh=0;
        for(int i=1;i<=n;i++){
            if(vis[i]||in_degree[i])continue;
            vis[i]=1;ans[++now]=i;hh=1;
            for(int j=1;j<=n;j++){
                if(vis[j]||!M[i][j])continue;
                in_degree[j]--;
            }
        }
        if(hh==0||now==n)break;
    }
    if(now==n){
        for(int i=1;i<=n;i++){
            printf("%d ",ans[i]);
        }printf("\n");return 0;
    }
    printf("there is a ring in the map\n");
}

时间复杂度为O(n^2)

优化：

普通代码直接每次从前往后找一遍，当然浪费时间了。
对于一个入度为0的点，把它删除后要减少其所连接的点的入度，假设这个时候那些点的入度变成0，也就是说只有刚才删除的那个点必须固定在这些点的前面，这个时候就直接把这个点也删了，就大大简化了时间复杂度，变为了O(V+E)

优化代码：

#include<iostream>
#include<string.h>
#include<algorithm>
#include<vector>
#include<stdio.h>
#include<queue>
#include<set>
using namespace std;

int in_degree[509];
int M[509][509];
int vis[509];
int ans[500],ar=0;
int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    while(m--){
        int a,b;scanf("%d%d",&a,&b);
        if(M[a][b]==0)in_degree[b]++;
        M[a][b]=1;
    }
    queue<int>Q;
    for(int i=1;i<=n;i++)if(in_degree[i]==0){
        Q.push(i);vis[i]=1;
    }
    while(!Q.empty()){
        int t=Q.front();Q.pop();
        ans[++ar]=t;
        for(int i=1;i<=n;i++){
            if(vis[i]||M[t][i]==0)continue;
            in_degree[i]--;
            if(in_degree[i]==0){
                Q.push(i);vis[i]=1;
            }
        }
    }
    if(ar!=n){printf("no\n");return 0;}
    for(int i=1;i<=n;i++){
        printf("%d",ans[i]);
        if(i==n)printf("\n");
        else printf(" ");
    }
}

加限制条件的拓扑排序

因为拓扑排序ans不为一，所以很多时候题目会要求输出多个ans中字典序最小的那个

例题：

zjnu 1413

题意：

给出多个选手的对战结果，求一个比赛排名，多个ans时按名字升序排

思路：
这里写图片描述
首先把所有入度为0 的点加入优先队列（保证了开始的点从小到大），在删除一个点使另一个点的入度为0时，那个点也加入优先队列（因为只要删除4以外的点所得到的0入度点，和4点不会有先后关系），此时如果加入的点比4小，那么当然是先处理那个点了
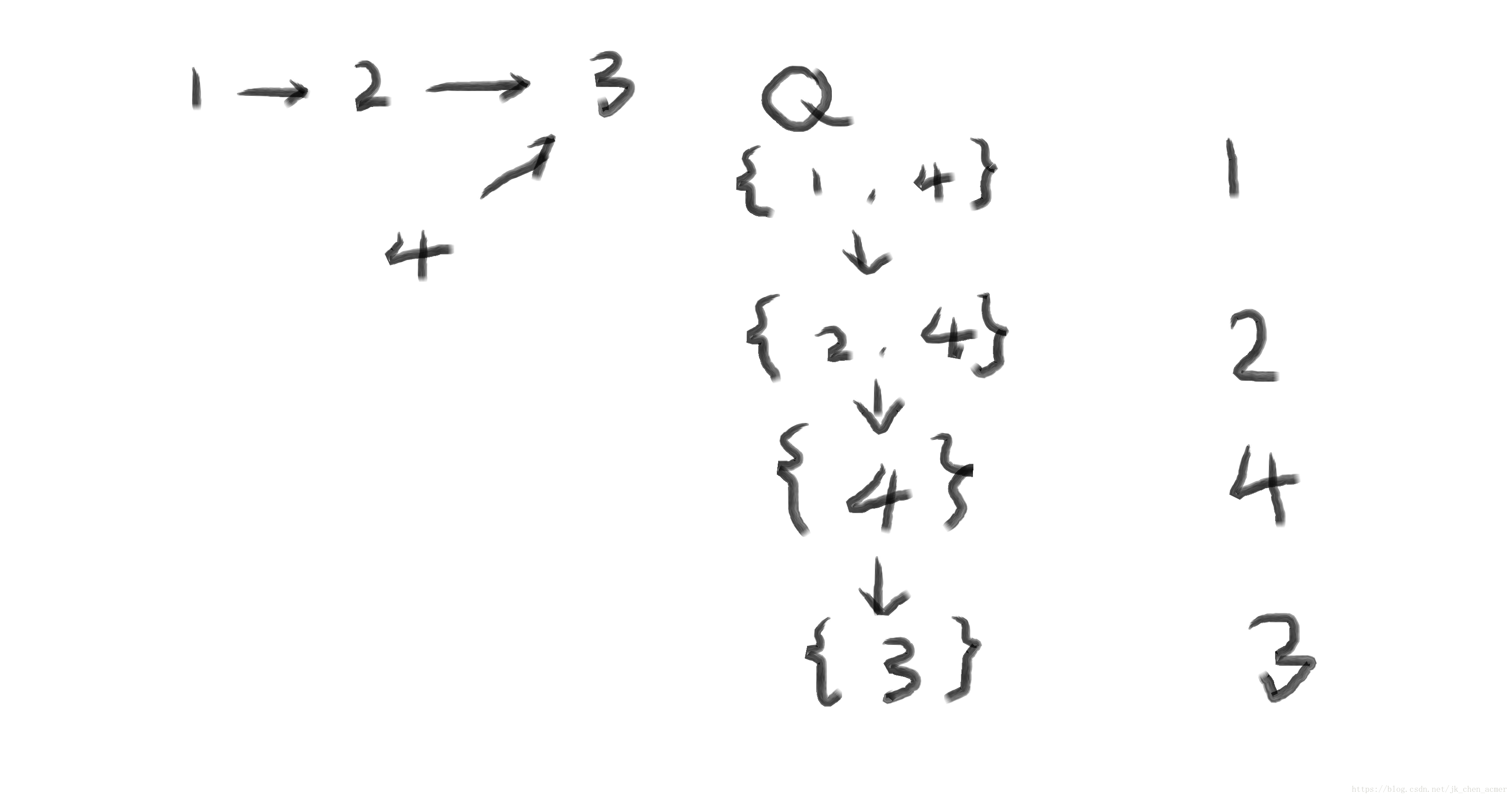
这里写图片描述

代码：

#include<iostream>
#include<string.h>
#include<algorithm>
#include<vector>
#include<stdio.h>
#include<queue>
#include<set>
using namespace std;

int in_degree[509];
int M[509][509];
int vis[509];
int main(){
    int n,m;
    while(scanf("%d%d",&n,&m)!=EOF){
        int ans[500],ar=0;
        for(int i=1;i<=n;i++)in_degree[i]=0;
        memset(M,0,sizeof(M));memset(vis,0,sizeof(vis));
        while(m--){
            int a,b;scanf("%d%d",&a,&b);
            if(M[a][b]==0)in_degree[b]++;
            M[a][b]=1;
        }
        priority_queue<int,vector<int>,greater<int> >Q;
        for(int i=1;i<=n;i++)if(in_degree[i]==0){
            Q.push(i);vis[i]=1;
        }
        while(!Q.empty()){
            int t=Q.top();Q.pop();
            ans[++ar]=t;
            for(int i=1;i<=n;i++){
                if(vis[i]||M[t][i]==0)continue;
                in_degree[i]--;
                if(in_degree[i]==0){
                    Q.push(i);vis[i]=1;
                }
            }
        }
        if(ar!=n){printf("no\n");continue;}
        for(int i=1;i<=n;i++){
            printf("%d",ans[i]);
            if(i==n)printf("\n");
            else printf(" ");
        }
    }
}