Java实现二叉树的前序、中序、后序输出

一、节点类

/**
 * @Auther: rll
 * @Date: 2021/10/9
 * @Description: 节点
 */
public class Node {
    //节点名称
    private String name;

    public Node(String name){
        this.name = name;
    }

    public String getName() {
        return name;
    }

    public void setName(String name) {
        this.name = name;
    }
}

二、二叉树类

/**
 * @Auther: rll
 * @Date: 2021/10/9
 * @Description: 二叉树
 */
public class BinaryTree {
    //根
    private Node root;
    //左
    private BinaryTree left;
    //右
    private BinaryTree right;

    public BinaryTree() {
    }

    public BinaryTree(Node root) {
        this.root = root;
    }

    public Node getRoot() {
        return root;
    }

    public void setRoot(Node root) {
        this.root = root;
    }

    public BinaryTree getLeft() {
        return left;
    }

    public void setLeft(BinaryTree left) {
        this.left = left;
    }

    public BinaryTree getRight() {
        return right;
    }

    public void setRight(BinaryTree right) {
        this.right = right;
    }

    /**
     * 生成树的节点
     *
     * @param node  根
     * @param left  左  null表示没有此节点
     * @param right 右  null表示没有此节点
     */
    public void makeTree(Node node, BinaryTree left, BinaryTree right) {
        this.setRoot(node);

        this.setLeft(left);

        this.setRight(right);
    }

    /**
     * @return 前序遍历输出   根左右
     */
    public String toPreOrderString() {
        StringBuilder sb = new StringBuilder();
        sb.append("{root=" + root.getName());
        if (null != left) {
            sb.append(",left=" + left.toPreOrderString());
        }

        if (null != right) {
            sb.append(",right=" + right.toPreOrderString());
        }
        sb.append("}");

        return sb.toString();
    }

    /**
     * @return 中序遍历输出   左根右
     */
    public String toMediumOrderString() {
        StringBuilder sb = new StringBuilder();
        sb.append("{");
        if (null != left) {
            sb.append("left=" + left.toMediumOrderString() + ",");
        }
        sb.append("root=" + root.getName());
        if (null != right) {
            sb.append(",right=" + right.toMediumOrderString());
        }
        sb.append("}");

        return sb.toString();
    }

    /**
     * @return 后序遍历输出   左右根
     */
    public String toPostOrderString() {
        StringBuilder sb = new StringBuilder();
        sb.append("{");
        if (null != left) {
            sb.append("left=" + left.toPostOrderString() + ",");
        }
        if (null != right) {
            sb.append("right=" + right.toPostOrderString() + ",");
        }
        sb.append("root=" + root.getName());
        sb.append("}");

        return sb.toString();
    }
}

 请注意，不要让Node.name为null ！

 二叉树原型

 

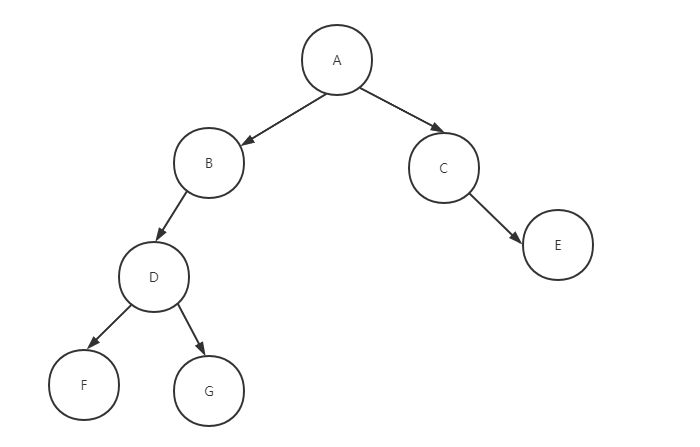
三、输出类

/**
 * @Auther: rll
 * @Date: 2021/10/9
 * @Description: 生成树并执行三种遍历方法
 */
public class PlayTree {

    public static void main(String[] args) {

        BinaryTree nt = new BinaryTree();

        Node nodeRoot = new Node("A");

        BinaryTree left = new BinaryTree();
        BinaryTree leftLeft = new BinaryTree();
        leftLeft.makeTree(new Node("D"),new BinaryTree(new Node("F")),new BinaryTree(new Node("G")));
        left.makeTree(new Node("B"),leftLeft,null);

        BinaryTree right = new BinaryTree();
        right.makeTree(new Node("C"),null,new BinaryTree(new Node("E")));

        nt.makeTree(nodeRoot, left, right);


        System.out.println("前序:");
        System.out.println(nt.toPreOrderString());
        System.out.println("中序:");
        System.out.println(nt.toMediumOrderString());
        System.out.println("后序:");
        System.out.println(nt.toPostOrderString());
    }
}

具体输出：