一步步改进Container With Most Water解法

题目描述

Given n non-negative integers a1, a2, ..., an , where each represents a point at coordinate (i, ai). n vertical lines are drawn such that the two endpoints of line i is at (i, ai) and (i, 0). Find two lines, which together with x-axis forms a container, such that the container contains the most water.

Note: You may not slant the container and n is at least 2.

题意分析

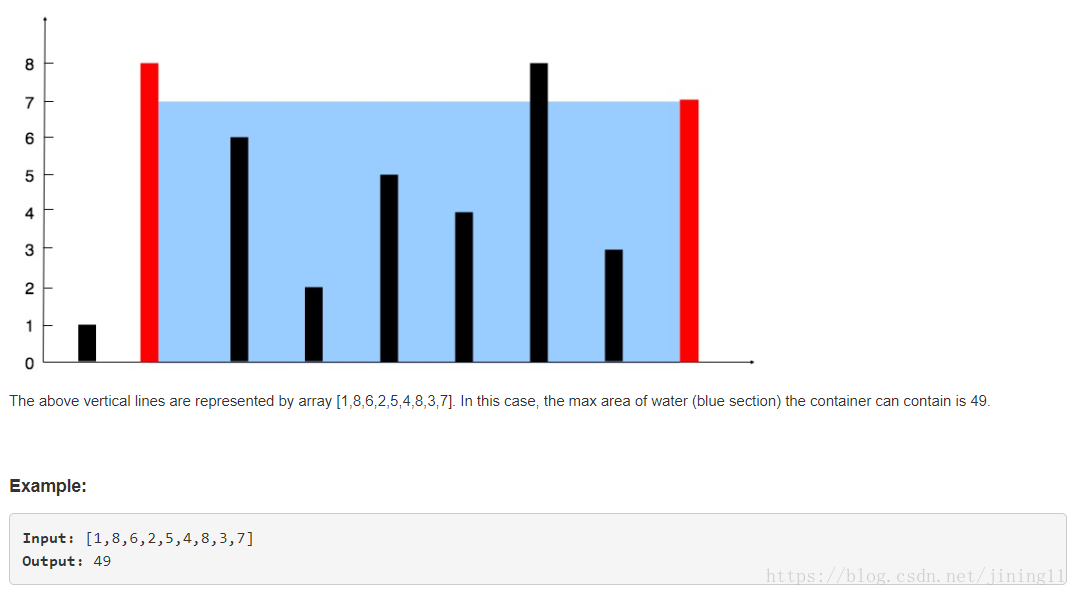
从上面这张示意图当中可以看出来，这道题从直观上来看就是“木桶原理”（一只木桶盛水的多少，并不取决于桶壁上最高的那块木块，而恰恰取决于桶壁上最短的那块）的变体。为了想象得更生动些，我们可以把图上那两根红柱子分别围绕着它们连线的中点旋转180°，获得两个半圆柱体，再将这两个圆柱体拼合成为一个水桶。水桶的容量等于底面积乘高，这里我们用两根柱子之间的距离代替底面积，而高度根据木桶原理就是较矮的那根柱子的高度。

于是这道题转化为如下描述：

在给定的一组数中找出这样两个数，使得它们之间较小的那个数与它们出现次序之差的乘积最大，并返回这个乘积。而在木桶效应中，短板是最重要的，在固定一个点作为木桶的短板之后，剩下我们需要找的，就是距离这个点最远的比它要大的点。

思路一：简单粗暴的遍历法

• 依次将每一个点作为短板
• 再次遍历寻找另一个目标点
• 计算当前围成水桶的容量
• 与记录的最大值比较，若超过则更新之

 

思路二：左右腾挪的圆规法

为了加速算法，一个很容易想到的办法就是分别从第一个元素往后以及从最后一个元素往前查找第一个比短板要长的元素，这样就可以得到在两个方向上距离短板点最远的长板。为了能在一个方向的遍历中利用另一个方向遍历的结果，特更新出圆规法如下。（自己瞎起的名字）

• 首先将‘圆规’的支点立于短板点
• 用笔尖在从距离短板点较远的一侧（比如说短板点在开头的话，就是从最后一个元素那里）到短板点之间的第一个大于短板点的点上做一个标记
• 将圆规掉转180度，在反方向做一个同样的标记
• 从另一侧到刚刚做的标记之间寻找比短板点更大的点，如果找到，新木桶的直径就是这一点到短板点之间的距离，否则，就是圆规两脚之间的距离
• 计算当前围成水桶的容量
• 与记录的最大值比较，若超过则更新之

class Solution {
public:
    int maxArea(vector<int>& height) {
        int max = 0;
        int l = height.size();
        int radius = 0;
        int n_area = 0;
        //计算前半段
        for (int i = 0; i < l/2; i++) {
        	if (height[i]*(l-i) < max) {
        		continue;
        	}
        	radius = 0;
        	for (int j = l-1; j > i; j--) {
        		if (height[j] >= height[i]) {
        			radius = j-i;
        			n_area = radius*height[i];
        			break;
        		}
        	}
        	for (int j = 0; j < i-radius; j++) {
        		if (height[j] >= height[i]) {
        			n_area = (i-j)*height[i];
        			break;
        		}
        	}
        	max = max > n_area ? max : n_area;
        }
        //计算后半段
        for (int i = l/2; i < l; i++) {
        	if (height[i]*i < max) {
        		continue;
        	}
        	radius = 0;
        	for (int j = 0; j < i; j++) {
        		if (height[j] >= height[i]) {
        			radius = i-j;
        			n_area = radius*height[i];
        			break;
        		}
        	}
        	for (int j = l-1; j > i+radius; j--) {
        		if (height[j] >= height[i]) {
        			n_area = (j-i)*height[i];
        			break;
        		}
        	}
        	max = max > n_area ? max : n_area;
        }
        return max;
    }
};

 

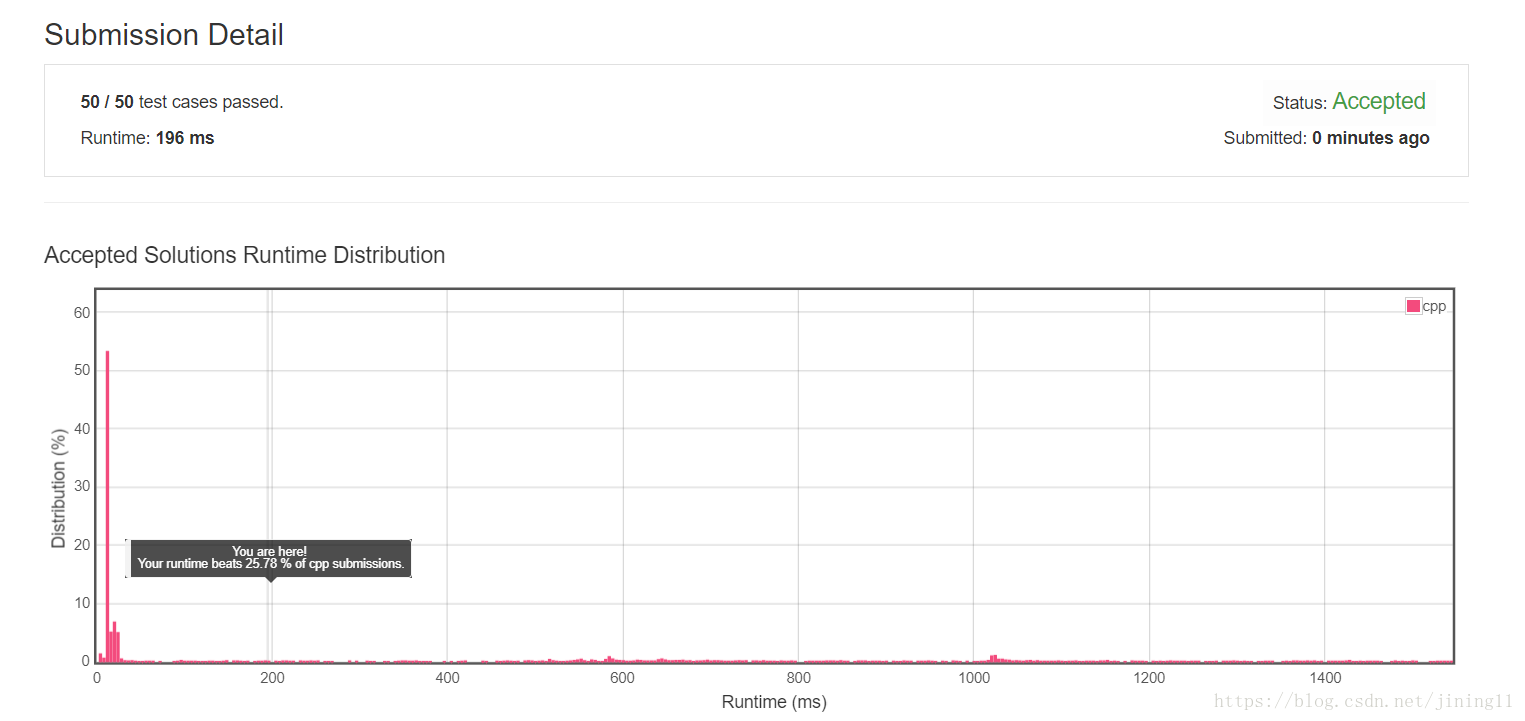
虽然过是过了，但运行时间好像不是很快，会不会有更好的方案呢？

 

思路三：来回变换的端点法

刚刚说的两个思路其实都有局限，就是每次都要指定一个点为短桶点，寻找另一个长桶点。其实可以从两端开始选点，分别向中间运动，短桶点和长桶点在两个端点之间来回变换。

• 将两个端点分别选为起始点
• 计算两个端点围成的体积
• 根据结果更新最大体积
• 两个端点中的短桶点向中心移动一步
• 重复上述步骤直至两个端点相遇

class Solution {
public:
    int maxArea(vector<int>& height) {
        int max = 0, n_area = 0, start = 0, end = height.size()-1, hs = 0, he = 0;
        while (start != end) {
        	hs = height[start], he = height[end], n_area = end-start;
            if (hs > he) {
                n_area *= he;
                end--;
            }
            else {
                n_area *= hs;
                start++;
            }
            max = max > n_area ? max : n_area;
        }
        return max;
    }
};

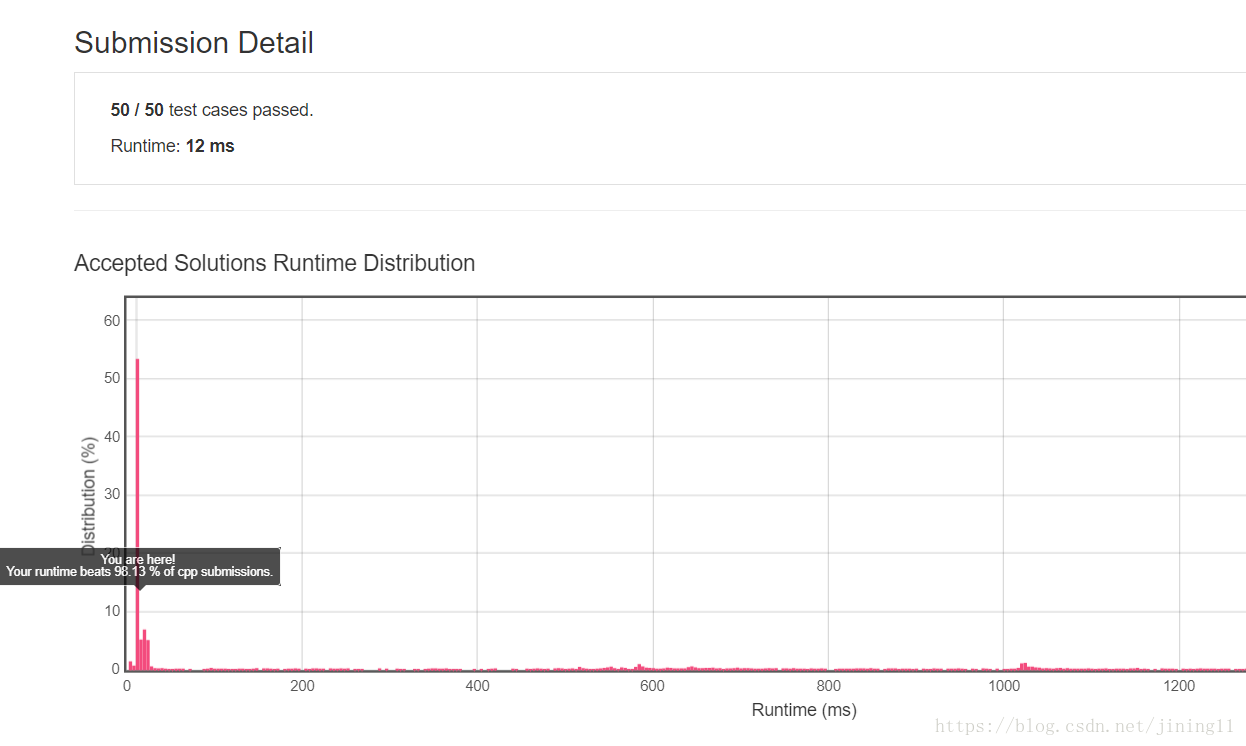
可以看到速度提升了许多。

注意事项

短桶点未必小于长桶点，判断时要注意包含两者相等的情况。