每日一题（第四天）

昨天团建太晚了没时间找没做过的题目补了qwq，虽然这道我没看题解也没做出来~

题目描述：众所周知，董学姐特别爱打太极，有一天打完太极没来得及换衣服就赶来培训（呜呜呜太感人了）。学长们看到董学姐的太极剑就两眼放光（有图为证）。可是董学姐认为他们太菜了，连一把强大的🗡都没有，不愿意和他们击剑。于是学长们想方设法找到了一把神奇的🗡，刚开始它的长度为1，这把剑有两个神奇的能力：（每使用一种能力需要耗时一天）
（1）可以从剑中挑选一把，并分裂成两把长度一模一样的剑。
（2）其中一把剑的剑长增长1。
学长们迫不及待的想与董学姐击剑了，他们想要🗡的总长大于n，你的任务是告诉学长们最少要消耗多少天可以使得🗡的总长大于n呢？
 

 

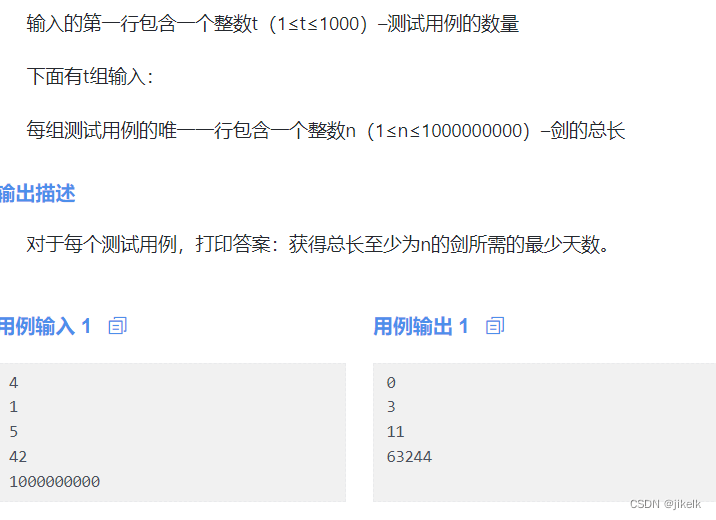
题目意思：就是给你一个长度为1的剑，然后有两个操作，使其中一把剑的长度++或者复制一把剑出来（每个操作要一天），求最短要几天。

这道题一开始我以为能用dfs和bfs能做，后来发现还是我太年轻了，看了题解才发现要贪心。

首先对于最少的天数n，把n分成 i 次增加操作和 j 次分裂操作 ，

这个可以贪心得到后分裂肯定是比先分裂得到的结果要高的。那么我们可以看成先连续的 i 次操作和连续的 j 次操作。

那么i和j的关系我们怎么判断呢？首先i次操作可以得到 长度为k的剑，然后连续的 j 次分裂，那么我们的总天数y就等于 k-1+n/k-1 或者 k-1+n/k  （如果n取余k就只需要-1次）。

然后求最小值的k的关系的话跟常数是并没有关系的 （改减还是减），就相当于  y=k+n/k ，是一个双钩函数（当k==n/k时，y最小）于是可以得出k为根号n时结果是最小，就可以求出具体的次数i和j。

代码如下：（抄了下姜哥的应该不会被发现吧（欸嘿））

#include<bits/stdc++.h>
using namespace std;
int main() {
	int _;
	cin >> _;
	while (_--) {
		int n;
		cin>>n;
		int sum=0,st=0;
		sum+=sqrt(n);//当前剑的总长度 
		st+=sqrt(n)-1;//当前的步数 
        st+=n/sum;// 5  6  
                if(!(n%sum))
                st--;
                cout<<st<<endl;
	}
	return 0;
}