离散数学上机实验二：集合上二元关系性质判定的实现

题目

通过编程实现集合上二元关系性质的判定以巩固相关理论的掌握

要求

对任意二元关系集合，判定其是否具有自反性、对称性、传递性、反对称性、反自反性，如果不具有某性质，需输出至少一个反例
输入：集合X的元素个数（不超过5个元素，必做）；X上关系的序偶个数（选做）
输出关系矩阵（由程序随机生成）
输出性质描述，不具备的性质需给出反例描述

示例

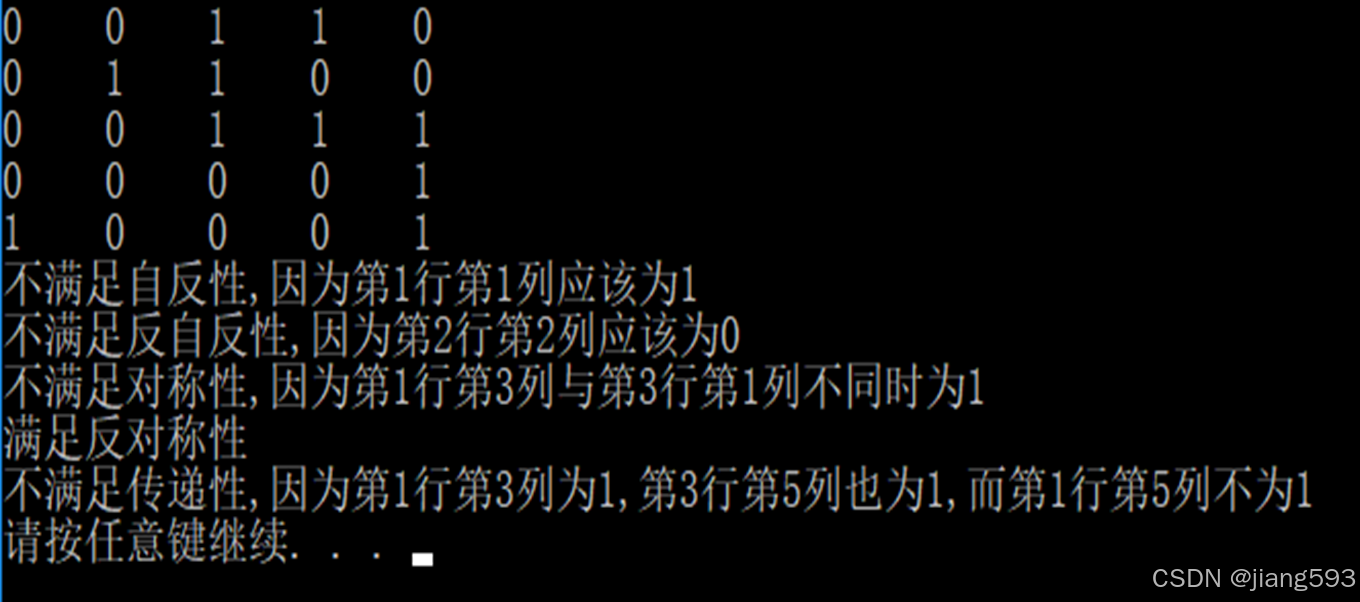
解答

用python实现

def reflexive(matrix):
    n = len(matrix)
    for i in range(n):
        if matrix[i][i] != 1:
            print(f"不满足自反性，第{i+1}行{i+1}列不满足自反性")
            return False
    print("满足自反性")
    return True

def irreflexive(matrix):
    n = len(matrix)
    for i in range(n):
        if matrix[i][i] != 0:
            print(f"不满足反自反性，第{i+1}行{i+1}列不满足反自反性")
            return False
    print("满足反自反性")
    return True

def symmetric(matrix):
    for i in range(n):
        for j in range(i,n):
            if matrix[i][j] != matrix[j][i]:
                print(f"不满足对称性，第{i+1}行{j+1}列为{matrix[i][j]}，第{j+1}行{i+1}列为{matrix[j][i]}，不对称")
                return False
    print("满足对称性")
    return True

def antisymmetric(matrix):
    for i in range(n):
        for j in range(i+1,n):
            if matrix[i][j]==1 and matrix[j][i]==1:
                print(f"不满足反对称性，第{i+1}行{j+1}列和第{j+1}行{i+1}列对称")
                return False
    print("满足反对称性")
    return True

def transitive(matrix):
    n = len(matrix)
    for i in range(n):
        for j in range(n):
            for z in range(n):
                if matrix[i][j] == 1 and matrix[j][z] == 1 and matrix[i][z] == 0:
                    print(f"不满足传递性，<i={i+1}, j={j+1}> 和 <j={j+1}, z={z+1}> 存在，但 <i={i+1}, z={z+1}> 不在关系中")
                    return False
    print("传递性")
    return True