分治算法分为快排和归并
快排
1、颜色分类
算法原理
将数组分为如下四个部分
[0,left] 0
[left+1,i-1] 1
[i,right-1] 未扫描元素
[right,size-1] 2 当nums[i]==0交换swap(nums[++left],nums[i++])
当nums[i]==1时 i++
当nums[i]==2时swap(nums[--right],nums[i]); 注意这里不要i++
代码
class Solution {
public:
void sortColors(vector<int>& nums) {
int i=0;
int left=-1,right=nums.size();
while(i<right)
{
if(nums[i]==0)
{
swap(nums[++left],nums[i++]);
}
else if(nums[i]==1)
{
i++;
}
else//nums[i]==2
{
//这里i不++,因为交换之后i位置上的是没有扫描过的元素
//[i,right-1]之间是没有扫过的元素
swap(nums[--right],nums[i]);
}
}
}
};
2、排序数组
算法原理
方法一:快排
方法二:归并排序
代码
class Solution {
public:
// void QuickSort(vector<int>& nums,int l,int r)
// {
// if(l>=r)
// return;
// int ra=rand();
// int left=l-1,right=r+1;
// //生成一个随机数来作为key
// int key=nums[ra%(r-l+1)+l];
// int i=l;
// while(i<right)
// {
// if(nums[i]<key)
// {
// swap(nums[++left],nums[i++]);
// }
// else if(nums[i]==key)
// {
// i++;
// }
// else
// {
// swap(nums[--right],nums[i]);
// }
// }
// QuickSort(nums,l,left);
// QuickSort(nums,right,r);
// }
vector<int> tmp;
void MergeSort(vector<int>& nums,int left,int right)
{
if(left>=right)
return;
//1、找中间节点
//这中间节点不一定是整个数组的中间节点,所以不要使用(right-left)/2
int mid=(right+left) /2;
//2、分发
MergeSort(nums, left, mid);
MergeSort(nums, mid + 1, right);
//3、合并数组
int cur1=left;
int cur2=mid+1;
int i=0;
while(cur1<=mid&&cur2<=right)
{
tmp[i++]=nums[cur1]<nums[cur2]?nums[cur1++]:nums[cur2++];
}
//4、处理没有的排序的数组
while(cur1<=mid)
{
tmp[i++]=nums[cur1++];
}
while(cur2<=right)
{
tmp[i++]=nums[cur2++];
}
//5、还原
for(int i=left;i<=right;i++)
{
nums[i]=tmp[i-left];
}
}
vector<int> sortArray(vector<int>& nums)
{
// 快排
// srand(time(NULL));
// int n=nums.size();
// int left=0,right=n-1;
// QuickSort(nums,left,right);
// return nums;
//归并排序
tmp.resize(nums.size());
MergeSort(nums,0,nums.size()-1);
return nums;
}
};3、数组中的第K个最大元素
215. 数组中的第K个最大元素 - 力扣(LeetCode)
算法原理:
方法一:优先级队列
优先级队列内部维护了一个堆排序,默认为大根堆,所以只需要把所有元素插入,然后把数据pop最后得到的结果就是第k大。
方法二:快排
1、将数组分为三个部分,数据个数分别为a,b,c
[0,left] <key a
[left+1,right-1] ==key b
[right,r] >key c
这里就可以分为三个情况
1) c>=k 直接在第三段区间找第k大
2) b+c>=k 说明在第二段区间,而第二段区间所有值都相等,直接返回key
3)如果1和2都不成立,那么在第一段区间找第k-b-c大
代码
//方法一
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
priority_queue<int> q;
for(auto e: nums)
{
q.push(e);
}
for(int i=0;i<k-1;i++)
{
q.pop();
}
return q.top();
}
};
//方法二
class Solution {
public:
int QucikSort(vector<int>& nums,int l,int r,int k)
{
int rad=rand();
int key=nums[l];
int i=l;
int left=l-1,right=r+1;
while(i<right)
{
if(nums[i]<key)
{
swap(nums[++left],nums[i++]);
}
else if(nums[i]==key)
{
i++;
}
else
{
swap(nums[--right],nums[i]);
}
}
int b=right-left-1;
int c=r-right+1;
if(c>=k)//到第三段区间去找第k大
{
return QucikSort(nums,right,r,k);
}
else if(b+c>=k)
{
return key;
}
else
{
return QucikSort(nums,l,left,k-b-c);
}
}
int findKthLargest(vector<int>& nums, int k) {
srand(time(NULL));
return QucikSort(nums,0,nums.size()-1,k);
}
};4、库存管理 III(最小的k个数)
LCR 159. 库存管理 III - 力扣(LeetCode)
算法原理
与上一道题类似,也可以使用优先级队列,建一个小根堆
这里也是分为三个情况,找最小的k个元素
1)k<a 在第一个区域找最小的k个元素
2)k<=a+b 直接返回,当前位置前面k个就是最小的元素
3)如果不是上面两种情况,就在第三个区域去找k-a-b个最小元素
本质就是快排,之所以在里面进行判断,这样把前k小个排出来就行,不需要关注这前k小的排序
代码
class Solution {
public:
void QuickSort(vector<int>& nums,int l,int r,int k)
{
int ra=rand();
int left=l-1,right=r+1;
//生成一个随机数来作为key
int key=nums[ra%(r-l+1)+l];
int i=l;
while(i<right)
{
if(nums[i]<key)
{
swap(nums[++left],nums[i++]);
}
else if(nums[i]==key)
{
i++;
}
else
{
swap(nums[--right],nums[i]);
}
}
//这里将数组分为三个区间
//个数分别为a,b,c
int b=right-left-1;
int a=left-l+1;
if(k<a)
{
QuickSort(nums,l,left,k);
}
else if(k<=a+b)//直接返回
{
return;
}
else//在c区间找k-a-b个
{
QuickSort(nums,right,r,k-a-b);
}
}
vector<int> inventoryManagement(vector<int>& stock, int cnt)
{
QuickSort(stock,0,stock.size()-1,cnt);
return {stock.begin(),stock.begin()+cnt};
}
};归并排序
5、交易逆序对的总数
LCR 170. 交易逆序对的总数 - 力扣(LeetCode)
算法原理:
采用归并排序的思想
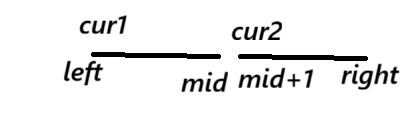
1、从中间将数组分为两个部分,先找左边有多少个逆序对,排序。
2、然后找右边的逆序对,排序
3、找左边和右边可以组成多少个逆序对
1)nums[cur1]>nums[cur2],说明cur1到mid之间的数都比cur2大,ret+=mid-cur1+1,cur2++
2)nums[cur1]<=nums[cur2],cur1++
3)当cur1==mid或者cur2==right,进行排序
注意:这里排序需要排升序,这样左边只要第一个比右边的大,那么左边所有就比右边大
代码
class Solution {
public:
int tmp[50010];
int MergeSort(vector<int>& nums,int left,int right)
{
int ret=0;
if(left>=right)
return 0;
//1、找中间节点
//这中间节点不一定是整个数组的中间节点,所以不要使用(right-left)/2
int mid=(right+left) /2;
//2、找到左边部分有多少个逆序对,然后排序
ret+=MergeSort(nums, left, mid);
//找到右边部分有多少个逆序对,然后排序
ret+=MergeSort(nums, mid + 1, right);
//3、一左一右
int cur1=left;
int cur2=mid+1;
int i=0;
while(cur1<=mid&&cur2<=right)
{
if(nums[cur1]>nums[cur2])
{
ret+=mid-cur1+1;
tmp[i++]=nums[cur2++];
}
else
{
tmp[i++]=nums[cur1++];
}
}
//4、处理没有的排序的数组
while(cur1<=mid)
{
tmp[i++]=nums[cur1++];
}
while(cur2<=right)
{
tmp[i++]=nums[cur2++];
}
//5、还原
//把排序后的数组插入原数组
//nums下标从left开始,tmp从0开始
for(int i=left;i<=right;i++)
{
nums[i]=tmp[i-left];
}
return ret;
}
int reversePairs(vector<int>& record) {
return MergeSort(record,0,record.size()-1);
}
};6、计算右侧小于当前元素的个数
315. 计算右侧小于当前元素的个数 - 力扣(LeetCode)
算法原理:
与第五题类似,上一道题找的是比右侧大的数,所以排升序
这道题降序排序,当左边的数比右边的第一个数大,说明左边比右边所有数都要大
注意:
1、需要记录原来的下标,使用index数组中的值来记录nums下标,当修改数据,index数组同步修改
2、ret数组,来记录返回值
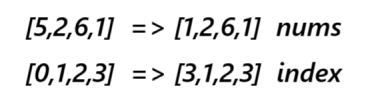
代码
class Solution {
public:
vector<int> ret;
vector<int> index;//在数组元素移动过程中,绑定数组原始下标
int tmp[500010];//存放临时元素
int tmp_index[500010];
void MergeSort(vector<int>& nums,int left,int right)
{
if(left>=right)
return;
//1、找中间节点
//这中间节点不一定是整个数组的中间节点,所以不要使用(right-left)/2
int mid=(right+left) /2;
//2、找到左边部分有多少个逆序对,然后排序
MergeSort(nums, left, mid);
//找到右边部分有多少个逆序对,然后排序
MergeSort(nums, mid + 1, right);
//3、一左一右
int cur1=left;
int cur2=mid+1;
int i=0;
while(cur1<=mid&&cur2<=right)
{
//使用index[cur1]来表示返回元素对应位置
if(nums[cur1]>nums[cur2])
{
ret[index[cur1]]+=right-cur2+1;
tmp_index[i]=index[cur1];//记录交换的位置
tmp[i++]=nums[cur1++];
}
else
{
tmp_index[i]=index[cur2];
tmp[i++]=nums[cur2++];
}
}
//4、处理没有的排序的数组
while(cur1<=mid)
{
tmp_index[i]=index[cur1];//第二次之后下标已经改变了,需要使用index[i]
tmp[i++]=nums[cur1++];
}
while(cur2<=right)
{
tmp_index[i]=index[cur2];
tmp[i++]=nums[cur2++];
}
//5、还原
for(int i=left;i<=right;i++)
{
nums[i]=tmp[i-left];
index[i]=tmp_index[i-left];
}
}
vector<int> countSmaller(vector<int>& nums)
{
int n=nums.size();
index.resize(n);
for(int i=0;i<nums.size();i++)
{
index[i]=i;
}
ret.resize(n);
if(nums.size()<=1)
return {0};
MergeSort(nums,0,n-1);
return ret;
}
};7、 翻转对
算法原理:
与上面题相同,直接排降序,然后进行判断
注意:
但是这里不可以像上面第六题一样,直接判断如果左边比右边第一个大,就比右边所有大,因为这里是比二倍大,排序是直接比大小
代码
class Solution {
public:
int tmp[50010];
int MergeSort(vector<int>& nums,int left,int right)
{
if(left>=right)
return 0;
int ret=0;
//1、找中间节点
//这中间节点不一定是整个数组的中间节点,所以不要使用(right-left)/2
int mid=(right+left) /2;
ret+=MergeSort(nums, left, mid);
ret+=MergeSort(nums, mid + 1, right);
int cur1=left;
int cur2=mid+1;
//降序
//这里先对两部分先进行翻转对判断
//因为这里需要计算,而排序是直接比较两个位置值的大小
while(cur1<=mid)
{
//2147483647 * 2 cannot be represented in type 'int'
//不要使用*
while(cur2<=right && nums[cur2]>=nums[cur1]/2.0)
{
cur2++;
}
if(cur2>right)
break;
cur1++;
ret+=right-cur2+1;
}
//4、合并数组
cur1=left;
cur2=mid+1;
int i=0;
while(cur1<=mid&&cur2<=right)
{
tmp[i++]=nums[cur1]>=nums[cur2]?nums[cur1++]:nums[cur2++];
}
while(cur1<=mid)
{
tmp[i++]=nums[cur1++];
}
while(cur2<=right)
{
tmp[i++]=nums[cur2++];
}
//5、还原
for(int i=left;i<=right;i++)
{
nums[i]=tmp[i-left];
}
return ret;
}
int reversePairs(vector<int>& nums) {
return MergeSort(nums,0,nums.size()-1);
}
};



















 3058
3058

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








