DualPivotQuicksort两枢轴快速排序

最新推荐文章于 2025-06-10 15:11:54 发布

转载最新推荐文章于 2025-06-10 15:11:54 发布 · 836 阅读

文章标签：

#DaulPivotQuickSort #双轴快速排序

算法与设计专栏收录该内容

36 篇文章

订阅专栏

本文详细解析了双枢轴快速排序算法的工作原理及其在Java JDK中的实现方式。相较于传统快速排序，双枢轴版本通过将数据划分为三部分来提高排序效率。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

参考jdk DualQuickSort源码
普通快速排序一次把数据划分成两部分，两部分再分别递归，两枢轴，就是两个结点，把数据划分成三部分，三部分再分别递归，可参考下图


            left part           center part                   right part
          +--------------------------------------------------------------+
          |  < pivot1   |    pivot1 <= && <= pivot2      |    > pivot2  |
          +--------------------------------------------------------------+
                        ^                                ^
                        |                                |
                       less                            great

划分成三部分：leftpart：x<p1，centerpart：p1<=x<=p2，rightpart:x>p2

注意：p1< p2
如何完成这个操作
程序中给的下图

        /*
         * Partitioning:
         *
         *   left part           center part                   right part
         * +--------------------------------------------------------------+
         * |  < pivot1  |  pivot1 <= && <= pivot2  |    ?    |  > pivot2  |
         * +--------------------------------------------------------------+
         *               ^                          ^       ^
         *               |                          |       |
         *              less                        k     great
         *
         * Invariants:
         *
         *              all in (left, less)   < pivot1
         *    pivot1 <= all in [less, k)     <= pivot2
         *              all in (great, right) > pivot2
         *
         * Pointer k is the first index of ?-part.
         */

less指向 < p1 的下一个位置
great指向 > p2 的前一个位置
k 是遍历的当前位置
less 到 k -1 之间的数：p1 <= x <= p2
对变量的当前k位置出现下面三种情况：
（1）ak < p1 交换 k 和less位置的数，less++
（2）ak < p1 && ak >p2 这个时候需要将 ak这个数放到对应的great的位置
程序中是先找到：A[great] < pivot2 的位置

while (A[great] > pivot2) { // 找到不满足条件的位置 
                     if (great-- == k) {
                         System.out.println("outer");
                         break outer;
                     }
                 }

再判断：A[great] < pivot1
若成立：这个时候说明great位置的数应该在在< p1 的部分

                if (A[great] < pivot1) { // a[great] <= pivot1，  

                     A[k] = A[less];  // less放到 k的位置,  k 位置的元素数保存在 ak中  
                     A[less] = A[great]; // great 放到less的位置 
                     ++less;  // 更新 less 
                 } else { // pivot1 <= a[great] <= pivot2
                     A[k] = A[great];
                 }

最后还有这个

A[great] = ak; // ak 放到 great位置 
--great;

上面的过程看着比较复杂，其实就是一个交换数的过程
若：A[great] < pivot1
A[less]位置说应该在中间部分，这里可以放到k的位置
A[great]应该放到less位置
又：ak这个数放到对应的great的位置
最后上面程序已经有了
若：A[great] >= pivot1 又：A[great] <= pivot2

A[k] = A[great];

A[great] = ak

就这样

结束后：形成最上面的形式，三个部分再分别进行递归
在jdk1.7中DualQuickSort 进行了优化
自己画的一个图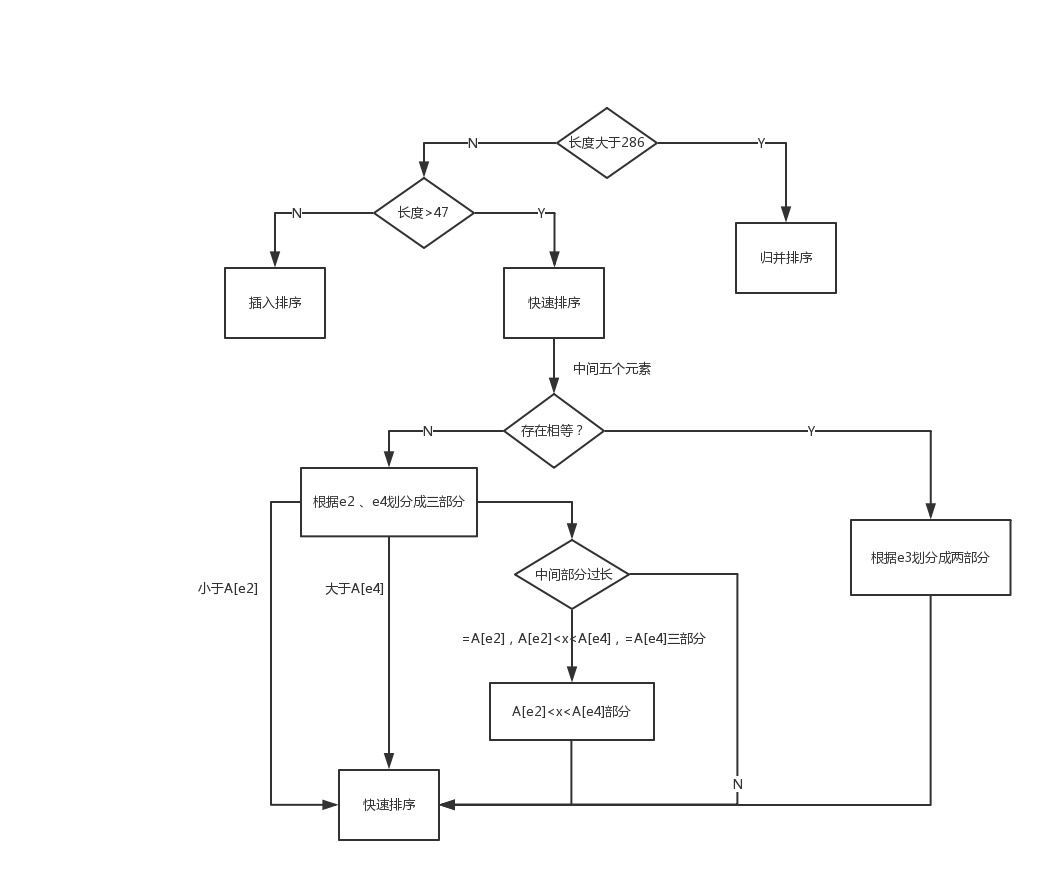
这里写图片描述
图中对run数组还没有理解，没有细画，在归并排序中会调用到快排的过长也没有画出来，因为这里都用到run数组，表示没理解。

下图中不是进行归并，而是进行快排递归

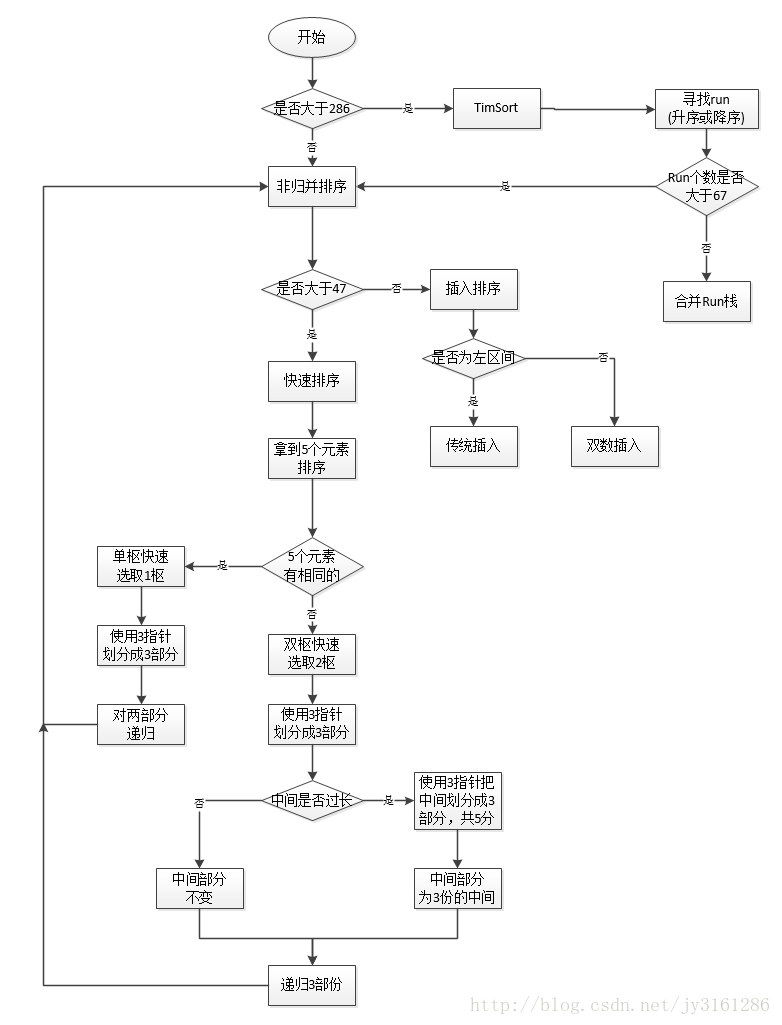
这里写图片描述

DualPivotQuicksort代码整理
由于p1 p2 两个值取得的左右端点的值，同时没有做相等判断，所有程序对没有相等数据可以实现排序

package alg.sort;

public class DualQuickSort {
    public void dualQuickSort(int[] A,int left,int right){
        if(left>=right)
        {
//          System.out.println(left+"\t"+right);
            return;
        }
        if(A[left]>A[right])
        {
            swap(A,left,right);
        }
        int less = left;
        int great = right;
        int pivot1 = A[left];
        int pivot2 = A[right];
        while (A[++less] < pivot1);
        while (A[--great] > pivot2);

        /*
         * Partitioning:
         *
         *   left part           center part                   right part
         * +--------------------------------------------------------------+
         * |  < pivot1  |  pivot1 <= && <= pivot2  |    ?    |  > pivot2  |
         * +--------------------------------------------------------------+
         *               ^                          ^       ^
         *               |                          |       |
         *              less                        k     great
         *
         * Invariants:
         *
         *              all in (left, less)   < pivot1
         *    pivot1 <= all in [less, k)     <= pivot2
         *              all in (great, right) > pivot2
         *
         * Pointer k is the first index of ?-part.
         */
        outer:
        for(int k = less - 1;++k<= great;){
            int ak = A[k];
            if(ak<pivot1){ // ak 小于 p1
                swap(A,k,less); // 交换
                less++;
            }else if(ak>pivot2){ // ak > p2 
                 while (A[great] > pivot2) { // 找到不满足条件的位置 
                     if (great-- == k) {
                         System.out.println("outer");
                         break outer;
                     }
                 }
                 if (A[great] < pivot1) { // a[great] <= pivot1，  

                     A[k] = A[less];  // less放到 k的位置,  k 位置的元素数保存在 ak中  
                     A[less] = A[great]; // great 放到less的位置 
                     ++less;  // 更新 less 
                 } else { // pivot1 <= a[great] <= pivot2
                     A[k] = A[great];
                 }
                 /*
                  * Here and below we use "a[i] = b; i--;" instead
                  * of "a[i--] = b;" due to performance issue.
                  */
                 A[great] = ak; // ak 放到 great位置 
                 --great;
            } // 其他情况就是中间位置，不用考虑 
        }

        System.out.println("left :"+left+" less " + less + " great" + great+" right "+ right);
        Print.printArray(A);    

        dualQuickSort(A,left,less-1);
        dualQuickSort(A,less,great);
        dualQuickSort(A,great+1,right);
    }
    public void swap(int[] A,int i,int j){
        int t = A[i];
        A[i] = A[j];
        A[j] = t;
    }
    public static void main(String[] args){
        int[] A = new int[]{13,3,65,97,76,10,35,71,5,7,3,27,49};
        Print.printArray(A);
        DualQuickSort dualQuickSort = new DualQuickSort();
        int l = 0;
        int r = A.length -1;
        dualQuickSort.dualQuickSort(A,l,r);
        Print.printArray(A);
    }

}