本文是HNUCM信息科学与工程学院第二届新生赛正式赛的题目解析。涵盖简单、中等、困难三类题目，包括字符串转换、电灯开关、数论、博弈、动态规划等问题，详细介绍了题目描述、输入输出要求，并给出部分题目的解题思路与代码。
HNUCM信息科学与工程学院第二届新生赛——正式赛
简单题
A：Yftc的字符串转换
题目描述
Ytfc来到了一个魔法密林，里面住着一只魔法兔子，Yftc想去见见这只魔法兔子，但是这个魔法密林很奇怪，你需要将手中的字符串小写变成大写，大写变成小写才能进入。
你能帮帮Yftc完成这个问题嘛？
输入
多组输入，每组一行，包含一个字符串，1<=字符串长度<=200
输出
每行输出一个大小写转换后的字符串。
样例输入
abcDE
ABCDE
样例输出
ABCde
abcde
代码
ASCII码的简单运用
#include<stdio.h>
#include<string.h>
int main()
{
char str[205] = { 0 };
int len;
while (scanf("%s", str) != EOF)
{
len = strlen(str);
for (int i = 0; i < len; i++)
{
if (str[i] >= 'a' && str[i] <= 'z')
str[i] -= 32;
else if (str[i] >= 'A' && str[i] <= 'Z')
str[i] += 32;
}
printf("%s\n", str);
memset(str, 0, len);
}
return 0;
}
C： XP的电灯
题目描述
XP最近发现一个很好玩的问题。现在有N盏电灯，序号为1到N，最开始的时候所有电灯都是关闭的。XP有一群同学，序号是（1~K）,这些调皮的同学会去按电灯的开关，每个同学按开关符合一种规律。序号为1的同学会按下序号是1的倍数的灯的开关，序号是2的同学会按下序号是2的倍数的灯的开关（将关的灯打开，开的灯关闭）。现在XP有K位同学，每位同学都去操作一次，问最后有多少盏灯是亮着的？
输入
每行输入两个整数，N，K（K<=N<=1000）
输出
每行输入一个整数，表示打开电灯的数量。
样例输入
2 2
10 10
样例输出
1
3
代码
按照题意模拟一遍过程就行
#include<stdio.h>
#include<string.h>
int num[1001];
int main()
{
int n, k;
while (~scanf("%d%d", &n, &k))
{
memset(num, 0, sizeof(num));
for (int i = 1; i <= k; i++)
{
for (int j = i; j <= n; j+=i)
{
num[j]++;
}
}
int ans = 0;
for (int i = 1; i <= n; i++)
{
if (num[i] % 2 == 1)
ans++;
}
printf("%d\n", ans);
}
return 0;
}
E： 小小yh的几何
题目描述
一个大圆中包含两个小圆，三个圆的圆心均位于同一水平直线。
输入
有多组数据，每行包含两个实数，分别表示两个蓝色圆的面积。s1,s2(1<=s<=100)
输出
绿色部分面积。(保留三位小数)
样例输入
3.140 3.140
样例输出
6.280
结果ans=pi*(r1+r2)^2-s1-s2=pi *r1 *r2 *2
#include<stdio.h>
#include<math.h>
#define pi 3.1415926
int main()
{
double a, b;
double ans;
while (scanf("%lf%lf", &a, &b) != EOF)
{
ans = sqrt(a * b) * 2;
printf("%.3lf\n", ans);
}
return 0;
}
F：我爱中国
题目描述
2019年是祖国70周年华诞，Sunny老师让我用我们专业的方式来表达一下对祖国的热爱！
输出“I love China”。
输入
无
输出
输出一行“I love China”
样例输入
样例输出
I love China
代码
真正的水题，甚至连多组输入都没有
#include<stdio.h>
int main()
{
printf("I love China\n");
return 0;
}
J：XP的绝对值
题目描述
XP今天要教他的初一妹妹绝对值，但是XP觉得这个太简单了，不想教她。于是XP想写一个程序，让妹妹手动输入，可以得出来答案。
输入
包含多组输入，每行一个值n。
输出
对于每组输入，你只需输出一行，每行一个值，表示n的绝对值。
样例输入
1
0
-1
样例输出
1
0
1
//n小于零取相反数就行
#include<stdio.h>
int main()
{
int n;
while (scanf("%d", &n) != EOF)
{
if (n < 0)
n = -n;
printf("%d\n", n);
}
return 0;
}
中等题
G：小小yh的数论
hyh最近迷上了数论，尤其对费马小定理情有独钟，最近他又发现利用费马小定理能够快速求出2^100除以13的余数
费马小定理定义如下：费马小定理(Fermats little theorem)是数论中的一个重要定理，在1636年提出。如果p是一个质数，而整数a不是p的倍数，则有a^（p-1）≡1（mod p）相信聪明的学弟学妹们一定能够从上面的计算过程中，快速求出p是一个质数且a不是p的倍数的情况下，(a^n)%p的答案
输入
有多组样例，每行包含三个整数a,n,p(2<=a<=9,1<=n<=1000000,2<=p<=14)
输入保证a,p互质。
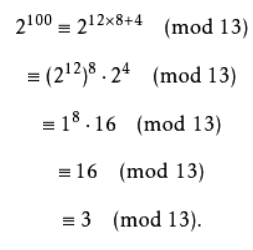
输出
每组数据输出一个整数,代表(a^n)%p后的值。
样例输入
2 100 13
样例输出
3
提示
质数是指在大于1的自然数中，除了1和它本身以外不再有其他因数的自然数。
9^13=2541865828329超出了int的数据范围
代码
仔细观察费马小定理和图片中的例子，2的100次方被分解为8个2的12次方乘以2的4次方，取模也就是取余有一个重要的性质，a*b%c=(a%c) *(b%c)%c，又因为212%13=1,所以式子变为24%13=3
由此我们可以先让n=n%(p-1)，然后再求2的n次方
费马小定理的证明网上有很多版本，这里提供一个我认为相对比较简单清晰的版本
#include<stdio.h>
int main()
{
long long a, n, p,ans;
while (~scanf("%lld%lld%lld", &a, &n, &p))
{
n = n % (p - 1);
ans = 1;
for (int i = 0; i < n; i++)
ans = ans * a % p;
printf("%lld\n", ans);
}
return 0;
}
H： yangftc的魔法
题目描述
yangftc会两种魔法，一个是将一个东西变多a份，另一个是将一个东西复制一倍，不过他只有b个单位的能量，每一种魔法都会消耗一单位的能量，yangftc现在有x个单位的钱，yangftc想让他的钱尽量多，你能告诉他他最多能有多少钱吗
输入
首先输入t代表样例数量
后跟t组样例每一个样例一行
每个样例输入三个数字a，b，x
输出
yangftc最多能拥有的钱数
数据范围 1<=t<=500 1<=a<=40 1<=b<=40 1<=x<=10
样例输入
1
1 2 1
样例输出
4
代码
直接将思路就能明白了，当x大于等于a的时候，我们让x翻倍，当x小于a的时候，就让x加上a
#include<stdio.h>
int main()
{
double x;
int t, a, b;
scanf("%d", &t);
while (t--)
{
scanf("%d%d%lf", &a, &b, &x);
while (b--)
{
if (x >= a)
x *= 2;
else
x += a;
}
printf("%.0lf\n", x);
}
return 0;
}
I：Yangftc&XP的博弈
题目描述
yangftc逃出魔法大陆后，发现自己在一片沙漠，旁边是XP，他是从另一个魔法大陆来的，而附近只有一瓶水，这只够一个人走出去，为了存活下来他们决定玩一个游戏来决定水的归属
他们找来一些石子（不用管他们怎么找过来的）放在一起变成一堆。如果这一堆石子个数为奇数则可以拿去一个或者两个石子，如果这一堆石子个数为偶数则只能拿去一个石子，两个人轮流进行操作，yangftc先手,取走最后一个石子的人胜，假设两个人都知道游戏的诀窍，判断yangftc是否能赢
输入
第一个数字t代表样例数量
后面t个样例，每一个样例输入一个整数n代表石子的个数
输出
yangftc能赢输出YES，否则输出NO
数据范围 1<=t<=500 1<=n<=100000
样例输入
2
2
3
样例输出
NO
YES
代码
分类讨论一下这题就是一个简单题
- 当石头数量为奇数时，yangftc先手拿一个石头让石头数变为偶数，那么XP接下来只能选一个石头，那么yangftc又可以像前面一样，只拿一个石头，最终因为石头数为奇数，那么yangftc会拿走最后一个石头，也就赢了
- 当石头数量为偶数时，yangftc先手只能拿一个石头让石头总数变为奇数，接着因为石头个数为奇数，和上面第一点的情况类似，只是这次等价于XP先手从奇数个石头中先手拿
- 总合在一起，就是奇数yangftc赢，偶数XP赢
#include<stdio.h>
int main()
{
int num;
int t;
scanf("%d", &t);
while (t--)
{
scanf("%d", &num);
if (num % 2 == 1)
printf("YES\n");
else
printf("NO\n");
}
return 0;
}
困难
这两个动态规划题当时都没有人做出，所以归为困难题
D：XP的宝藏
题目描述
几经波折和磨难，XP终于拿到了宝库的钥匙和藏宝图，他站在宝库的左上角，这是宝库的入口，出口在右下角。宝库是由一个个小暗格组成的正方形，有些暗格里面有宝藏，也有一些暗格没有。暗格中布满了机关，所有开往左边和上面的门都不能开启，一旦开启就会触发机关，将被万箭穿心。XP开始陷入深深的沉思，他希望活着走出宝库；人总是有贪欲的，他还希望能够带走尽可能多的宝藏，你能否帮到他呢？
输入
每组输入第一个包括一个N，表示N*N的矩阵
第2~n+1行表示该藏宝图 （0<=N<=20）
输出
XP获得的最多宝藏数
样例输入
3
1 10 2
2 1 1
20 1 1
样例输出
25
代码
这个题和下面的B题XP的午餐都被叫做动态规划题(简称dp），不像I题的博弈论和H题的贪心思想，这种思想要是没有学过是很难自己领悟一二的。
表达能力优先，尽量长话短说，把要点体现出来，结合代码慢慢体会
首先把这个藏宝图输入，是一个二维矩阵，dp (i,j)就表示从之前的某个点走到这个点的最大宝藏。由题意可知道这个点只可能是从上或者左边的某个点过渡而来，只需要判断这两个点dp(i-1,j),dp(i,j-1)的大小，然后加上去即可。
#include<stdio.h>
#include<string.h>
int map[25][25],dp[25][25];
int max(int a, int b)
{
return a > b ? a : b;
}
int main()
{
int n;
while (scanf("%d", &n) != EOF)
{
memset(dp, 0, sizeof(dp));
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
scanf("%d", &map[i][j]);
for(int i=1;i<=n;i++)
for (int j = 1; j <= n; j++)
{
dp[i][j] = max(map[i][j] + dp[i - 1][j], map[i][j] + dp[i][j - 1]);
}
printf("%d\n", dp[n][n]);
}
return 0;
}
B：XP的午餐
题目描述
XP每天都会思考一个问题，今天午餐去哪里吃？这是一个很重要的问题，这会影响到他下午的体力值。他的午餐预算是M元，现在有N种菜品，每一种菜品的价格和能够提供的体力值已知（每种菜品只能选择一次），请问如何选择菜品能够让XP下午的体力值最大呢？
输入
多组输入
第一行：M元和菜品数量N。
接下来N行，每一行两个整数，分别表示每一种菜品的价格(vi)和能够获得的体力值(wi)。
（0<N<=20,0<=M<=1000）(0<=vi<=50，0<=wi<=100)
输出
最大体力值。
样例输入
10 5
1 5
2 4
3 3
4 2
5 1
样例输出
14
上面那个题要是没学过还有可能写出来，这个经典的01背包的动态规划问题就是不友好了，最近刚好在复习dp的一些内容，到时候抽时间写一个专门讲解01背包和基础dp的文章，再把链接放在这，这里直接上代码
对dp感兴趣可以看看罗勇军老师的这篇介绍常见dp的博客
罗勇军老师的dp专题
#include<stdio.h>
#include<string.h>
struct x {
int v, w;
}food[25];
int n, m;
int dp[110][1010];
int max(int a, int b)
{
return a > b ? a : b;
}
int ans() {
memset(dp, 0, sizeof(dp));
for (int i = 1; i <= n; i++)
for (int j = 0; j <= m; j++)
if (food[i].v > j)
dp[i][j] = dp[i - 1][j];
else
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - food[i].v] + food[i].w);
return dp[n][m];
}
int main()
{
while (~scanf("%d%d", &m, &n))
{
for (int i = 1; i <= n; i++)
scanf("%d%d", &food[i].v,&food[i].w);
printf("%d\n", ans());
}
return 0;
}
扫一扫
696
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
