BST、AVL、B-、B+、红黑树的基本定义和结构

BST

即二叉搜索树

基本定义：

• 对于任意一个节点，若有左子树，则左子树的所有节点都小于当前节点；若有右节点，则所有右节点都大于当前节点，即满足递归定义。

AVL

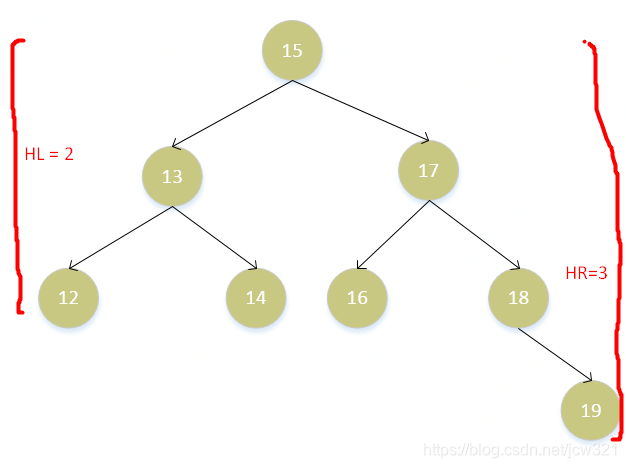
即平衡二叉搜索树

基本定义:

• 二叉搜索树(BST)的性质，平衡二叉搜索树也满足；
• 对于任意一个节点，若其左子树的树高为HL，其右子树的树高为HR，则||HL-HR|| < 2

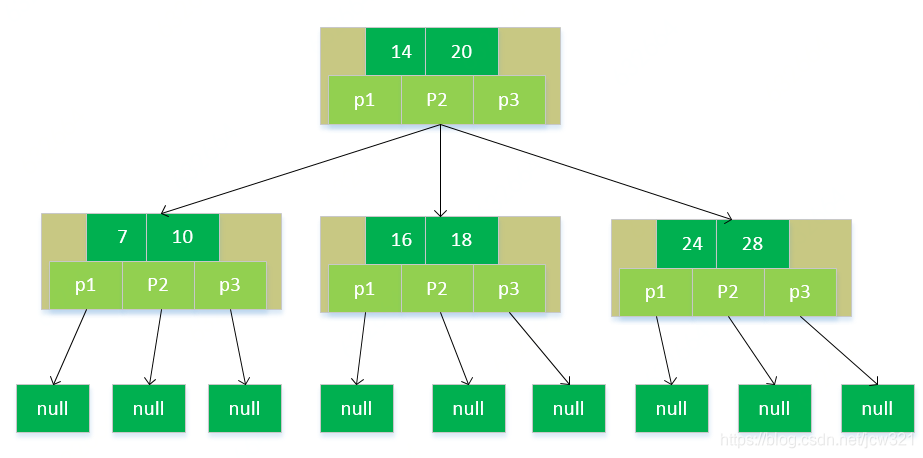
B-树

基本定义：（M阶B-树）

• 对于节点（p0,k1,p1,k2…,kn,pn）,pi节点下的值都小于k(i+1), ki< pi节点下的值 < ki+1 (i >=1)
• 除非根节点是叶子节点，否则至少有两个节点；
• 每个节点至多有M个子节点，即每个节点至多有M-1个关键字key；
• 有K个子节点的非叶子节点包含K-1个健；
• 每个非叶子节点（根节点除外）至少有M/2（向上取整）个子节点；
• 所有的叶子节点都在同一层

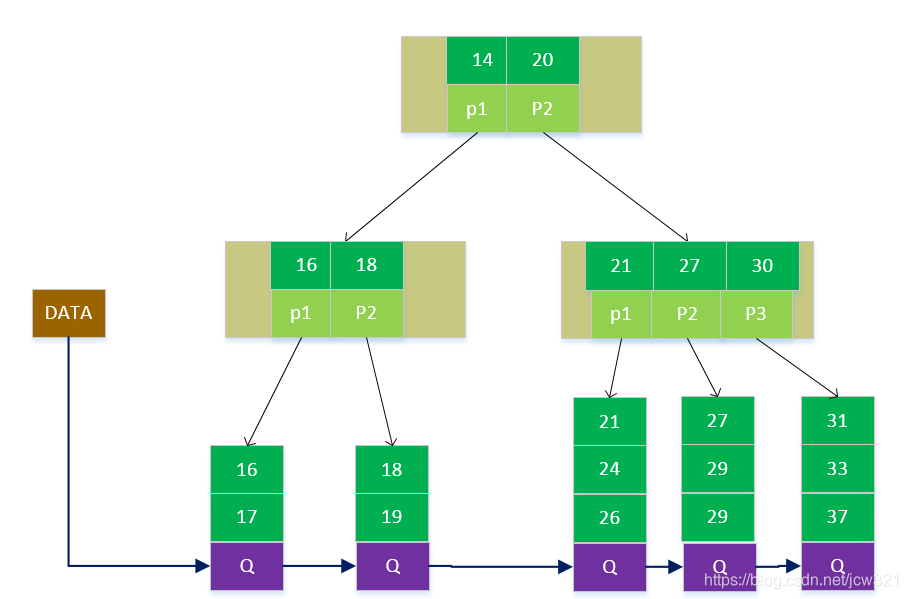
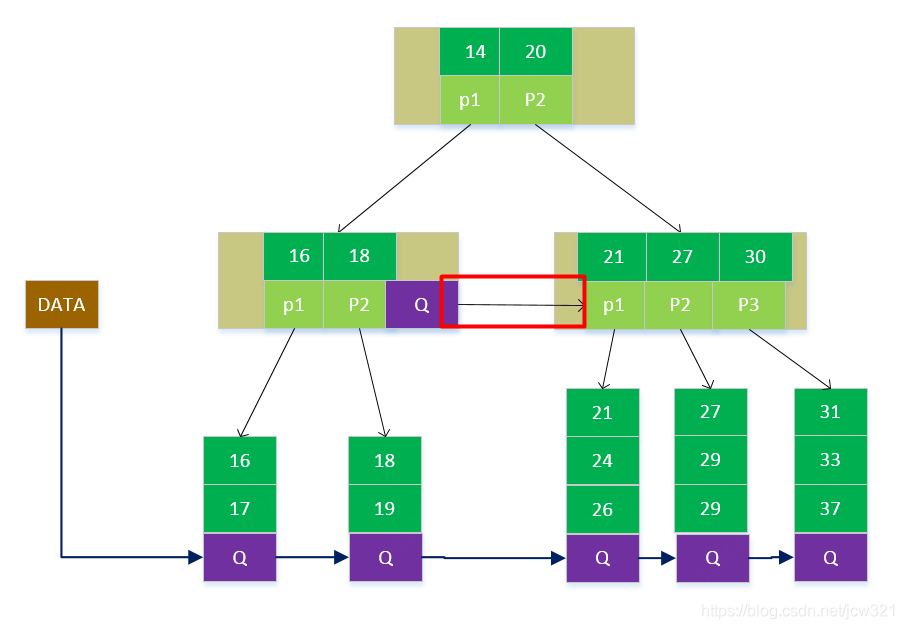
B+树

基本性质：

• 除了下面一些条件和B-树不同外，其他基本性质和B-树相同；
• 所有的关键字都出现在叶子节点的链表中，且链表中的关键字恰好是有序的；
• 有K个子树的节点包含K个元素，且这K个元素不保存数据，只用来作为索引，所有的数据都保存在叶子节点上；
• 所有的中间节点元素都同时存在于子节点，在子节点元素中是最大（或最小）元素。
• 为所有的叶子节点增加一个链指针；

B*树

基本性质:

• 非叶子节点的兄弟节点之间加入了一个指针，其他的性质和B+树相同；

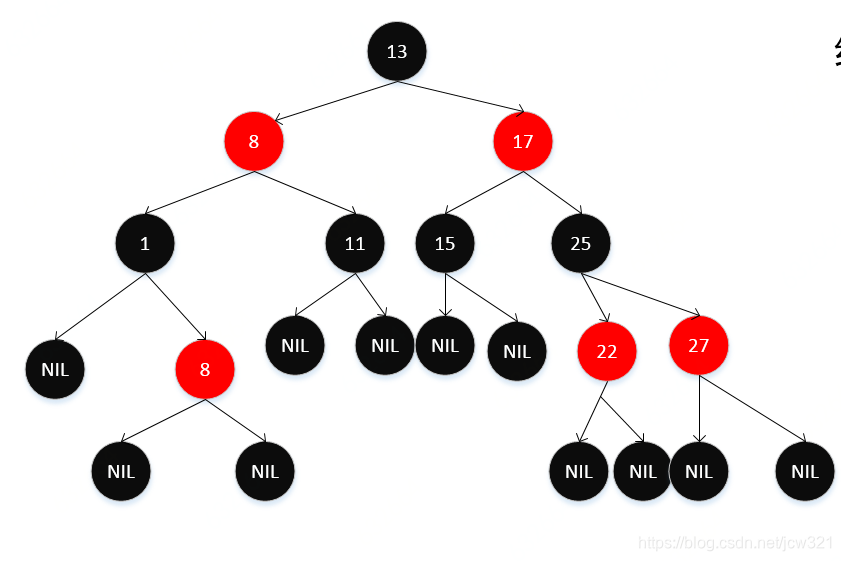
红黑树

基本性质：

• 每个节点是黑色的或者红色的；
• 根节点是黑色的；
• 每个叶子节点（NIL）是黑色的；
• 如果一个节点是红色的，则其两个儿子节点都是黑色的；
• 对于每一个节点，从该节点到其所有子孙叶子节点具有相同数目的黑色节点；