本文详细介绍了算法竞赛中的小技巧，包括快读、STL的使用、iostream的注意事项、algorithm库中的函数应用，以及一些常用数据结构如pair、vector、queue、stack、set、map和unordered_map的操作。还涵盖了前缀和、双指针算法、高精度计算、二进制与倍增等算法。此外，文章还强调了易错点，提供了各种实用的代码示例和技巧。
算法题的小技巧（持续更新）
本文将提及：
- 快读！
- STL几个重要函数的实际应用
- 容易错的
- 前缀和与差分
- 双指针算法
- 高精度加减乘除乘方
- 二进制与倍增(LCA,RMQ）
- 区间合并
- 快速幂，矩阵快速幂
- 离散化
- 贪心（因为贪心能讲的比较少，是个试出感觉和典型例题堆出来的算法，就在小技巧讲掉吧）
- 启发式合并
- 分块
- 拆点
- 莫队算法(树上莫队)
- 对拍与debug技巧
如果本文对你有帮助，记得点赞！
快读
单个字符的处理比数字快，于是我们把数字当成字符来读。（要读很大的数据的时候可以节省很多时间）
template<typename T>inline void read(T &x)
{
x=0;T f=1,ch=getchar();
while(!isdigit(ch)) {if(ch=='-') f=-1; ch=getchar();}
while(isdigit(ch)) {x=x*10+ch-'0'; ch=getchar();}
x*=f;
}
STL
参考了《算法竞赛进阶指南》stl部分和若干博客。
头文件可以用bits/stdc++.h
iostream
另：输入if else if的时候一定要把整个补全！
ios::sync_with_stdio(false);
while(cin>>n,n)//用于判断输入是否为0终止
cin>>op>>x;
if(op=="A")//用于多操作
cout.precision(2);//设置输出精度
algorithm
#include<algorithm>
//对序列进行的一系列基本操作
- sort
像sort，reverse之类，都是针对一个左闭右开的区间。
如对一个从a[0]到a[n-1]的数组排序，我们总是这么写:
sort(a,a+n);
如果是a[1]到a[n]:
sort(a+1,a+n+1)
如果是对vector
sort（v.begin(),v.end()）即可。
对pair排序时默认先对first再对second排序。
sort的第三个参数是一个cmp函数，用于我们对比较进行定义，也可以对小于号进行重载来实现这个功能。常用于你写了一个结构体，要对他们的实体排序的情况。
举个栗子：
int example[N];
vector<int> vecample;
bool cmp(int a,int b)
{
return a>b;
}
sort(example,example+n);
sort(vecample.begin(),vecample.end());
再举个栗子：
struct haha{
int x,y;
}s[N];
bool operator <(const haha &a,const haha &b)
{
return a.x>b.x||a.x<b.x&&a.y<b.y;
}
sort(s,s+n);
- lower_bound()/upper_bound()
首先使用这两个函数的数组必须是有序的。
这是两个二分查找的函数，lower_bound()返回第一个大于等于x的最小元素。
upper_bound()返回第一个大于x的元素。
使用嘛就是lower_bound(a,a+n,x)啦，是不是非常简单呢？
但是有人可能会疑惑，都是查找大于等于x的元素，为什么一个是lower一个是upper？
因为upper是用来倒过来算小于等于x的最大元素的。
举个栗子：
在有序int数组中查找大于等于x的最小整数的下标
int i=lower_bound(a,a+n,x)-a;
再举个栗子：
在有序vector中查找小于x的最大整数
int y=*--upper_bound(a.begin(),a.end(),x);
- next_permutation
把指定部分看成一个排列，求出这些元素构成的全排列中，字典序排在下一个的排列，直接在序列上更新。
若不存在返回false
举个栗子：求1~n的全排列
for(int i=1;i<=n;a[i]=i,i++);
do{
for(int i=1;i<=n;i++) cout<<a[i]<<' ';
cout<<endl;
}while(next_permutation(a+1,a+n+1);)
- unique
去重，这个离散化很常用了。
和sort一样左闭右开。
计算去重后的个数：
int m=unique(a.begin(),a.end())-a.begin();
int m=unique(a,a+n)-a;
离散化：
erase(unique(a.begin(),a.end()),a.end());
关于离散化
- reverse
翻转，没什么好说的。
和sort一样左闭右开。
reverse(a.begin(),a.end());
reverse(a,a+n);
- __gcd(a,b)//前面有两个横
cstring
#include<cstring>
- 写在前面：c++中string的效率很低，能用字符数组就不要用string了。
- memset
只能清零或者-1，或者0x3f，0xcf。
但是注意0x3f，0xcf的值有时候会被修改，要灵活进行判定。比如floyd算法中：if(d[i][j]>2*INF)。
如果是bool数组，bool是一字节的可以直接赋值。比如
memset(a,1,sizeof a);
- strcpy
两个变量，前一个是要复制到的目标数组起始地址，后一个是被复制的原数组起始地址，不要写反了。。
举个栗子：
char str1[]="sample";
char str2[40];
char str3[40];
strcpy(str2,str1);
strcpy(str3,"successful");
- strncpy
指定位数的strcpy.最后要自己补充\0
strncopy(str2,str1,sizeof(str2));
strncpy(str3,str2,5);
str3[5]=''\0';
- strcat
字符串连接
strcpy(str,"this ");
strcat(str,"is ");
strcat(str,"cat.");
- strncat
指定位数的字符串连接
strcpy(str1,"examp");
strcpy(str2,"leeeee");
strncat(str1,str2,2);
- strcmp
=0表示相等。
strcmp(key,buffer)!=0
- strchr
找出第一个此字母在字符串中的位置。
当然找所有也是可以写的，代码如下：
char str[]="this is a sample."
key[i]=strchr(str,'s');
while(key!=Null)
{
key[++i]=strchr(key[i-1]+1,'s');
}
- strstr
找出第一个此字符串在原字符串中的位置。
char str[]="this is a sample."
key=strstr(str,"sample");
- strlen
求长度，不包括\0
这些知识只是最初级的字符串处理办法，还有回文串，模式匹配串需要处理。
简单提及一些经典的字符串算法，在以后我的博文中也会提及。
- KMP(周期问题)
- Trie(异或问题)
- LCP
- Manacher(回文串)
- 字符串哈希（后缀树，后缀数组（波兰表），后缀自动机，后缀仙人掌）
- 有限状态自动机
- AC自动机
bitset
#include<bitset>
//声明：
bitset<10000> s;
//赋值
s[0]=1;
bitset相当于二进制压缩，n位bitset做一次位运算复杂度只有n/32.
- count
返回有多少位为1
- any/none
若s所有位为0，s.none()=true；s.any()=false;
若s有一位为1，s.any()=true;s.none()=false;
- set/reset/flip
s.set():把所有位变为1
s.set(k,v):把第k位变成v
s.reset():把所有位变为0
s.reset(k):把第k位变成0
s.flip():所有位取反
s.flip(k):第k位取反
讲一些位运算基本操作：
- (n>>k)&1 取出第k位
- n&((1<<k)-1) 取后k位
- n^(1<<k) 第k位取反
- n|(1<<k) 第k位赋值1
- n&(~(1<<k)) 第k位赋值0
- n&(-n) 取最右边的1的左边一个数
- x&(x+1) 把右边连续的1变成0
- x|(x+1)把右边连续的0变成1
- (x^(x+1))>>1 去掉右边连续的1
- x&(x-1)==0偶数，!=0奇数
- (x&y)+((x^y)>>1)位运算求平均数
- 位运算求两数之和：
int Add(int a,int b)
{
if(b==0) return a;//直到没有进位为止
int sum,carry;
sum=a^b;//完成没有进位的加法运算
carry=(a+b)<<1;//进位左移
return Add(sum,cacrry);
}
- 位运算统计1的个数
int num(int n)
{
int t=0;
while(n)
{
t++;
n=n&(n-1);
}
return tl
}
这些在最短hamildon路径，二进制枚举，状态压缩，树状数组lowbit函数都有应用。在二进制与倍增那一节会提及。
一些数据结构的头文件
这些因为比较容易理解，直接上例子，读者可以自行调试比较结果来掌握这些数据结构。
pair
我们先来讲一下pair这也是个常用的结构，不过不需要头文件。
pair是存两个数的结构体的简单写法，有first和second。比较的时候默认先比较first和second，多用于一个区间有l和r，把这两个都存下来。比如贪心法的活动安排问题，经典的区间合并问题。
还可以直接开pair数组，或者用其他数据结构套pair。
pair<int,int> p[N];
vector
vector是个变长的动态数组，数组中可以放数，字符串，pair，结构体等等。
vector不是链表，虽然他也接受随机存取，但是并不是o（1）的，因此我们总是在最后存数或者取数。
声明：
vector<int> a;
vector<int> b[233];
vector<rec> c;
基本函数：
empty和size是所有数据结构共享的。
a.size()
a.empty()
a.clear()
a.front()//a[0] *a.begin()
a.back()//*--a.end() a[a.size()-1]
a.push_back(x)
a.pop_back()
迭代器：
迭代器就像STL容器的指针，可以用*操作符解除引用
迭代器之间可以相加减，也可以与整数相加减。
a.begin()返回指向第一个元素的迭代器、
所有的容器都可以视作一个前闭后开的结构，a.end()返回vector最后一个元素再往后的边界。
*a.end()与a[n]一样是越界访问。
用迭代器遍历整个vector：
for(vector<int>::iterator it=a.begin();it!=a.end();it++)
{
cout<<*it<<endl;
}
迭代器不仅仅在vector可以用，其余数据结构里都可以。
实例：vector模拟邻接表
vector<int> ver[N],edge[N];
void add(int x,int y,int z)
{
ver[x].push_back(y);
edge[x].push_back(z);
}
for(int i=0;i<ver[x].size();i++)
{
int y=ver[x][i],z=edge[x][i];
}
【我记得蓝桥杯国赛训练营图论都是vector写的，可以都贴上来】
其实图论更常用的是链式前向星（数组模拟邻接表），先不写了以后写。
queue
其中包含queue和priority_queue
对于正常的队列，有方法：push,pop,front,back
队列涉及的知识点很多，像循环队列，双端队列，优先队列，spfa，bfs，单调队列等。
对于优先队列，有方法push，pop，top
优先队列可以重载运算符，重载的也是小于号，在讲sort的时候说过了。
priority_queue可以实现大根堆，如果需要实现小根堆，把要插入的元素取相反数插入，取出后再还原。另一种思路priority_queue<int,vector,greater>。
priority_queue<PII,vector<PII>,greater<PII>> pq;
//清空
while(!pq.empty()) pq.pop();
当优先队列里是pair的时候，如果用定义greater，则first和second都会逆序，如果只需要first逆序，second正序，还是用负号模拟小根堆。
堆还是要会手写的，因为priority_queue只能做到查找最大值O(1)，插入O(logn)，删除根O(logn)，而手写堆可以做到修改O(logn)，删除任意一个。
其中最重要的操作是up()和down()。
【以后做到题目再补充代码吧】
另外，优先队列也能实现分支限界法。
懒惰删除法。
单调栈和单调队列O(n)
一般先想暴力，如果具有符合单调栈或者单调队列的一种单调性，则尝试思考这两种数据结构。
单调栈用的是stack，如果不单调就把前面的弹出去。
应用场景查找左（右）侧第一个比他大（小）的数
有个往长方形上贴广告面积（或者只算块数）的裸题
int n=hight.size();
vector<int> stk;
for(int i=0;i<n;i++)
{
while(stk.size()&&heights[stk.top()]>=heights[i]) stk.pop();
if(stk.empty()) left.push_back(-1);
else left.push_back(stk.top());
stk.pop();
stk.push(i);
}
while(stk.size()) stk.pop();
for(int i=n-1;i>=0;i++)//right不能用pushback会发生翻转问题
{
while(stk.size()&&heights[stk.top()]>=heights[i]) stk.pop();
if(stk.empty()) right[i]=n;
else right[i]=stk.top();
stk.push(i);
}
int res=0;
for(int i=0;i<n;i++) res=max(res,heights[i]*(right[i]-left[i]-1));
return res;
接雨水：按层计算。重点是，栈里面还没完全空的时候，加上一个细长的长方形的面积
int trap(vector<int> &height)
{
int res=0;
stack<int> stk;
for(int i=0;i<height.size();i++)
{
int last=0;//存一下上一层的状态方便求高度差
while(stk.size()&&height[stk.top()]<height[i])//栈不空，并且单调递增，删掉栈顶
{
int t=stk.top();
stk.pop();
res+=(i-t-1)*(height[t]-last);//删掉的时候需要加上一个小长方形
last=height[t];//last更新成当前层
}
if(stk.size()) res+=(i-stk.top()-1)*(height[i]-last);//加上图中黑色细层
stk.push(i)
}
return res;
}
单调队列其实就是个可以pop_front的单调栈，我们利用deque实现。
应用场景：解决滑动窗口问题。
滑动窗口裸题：
vector<int> res;
deque<int> q;
for(int i=0;i<nums.size();i++)
{
if(q.size()&&i-k>q.front()) q.pop_front();
while(q.size()&&nums[q.back()]<=nums[i]) q.pop_back();//其实也就像一个队头会出队的单调栈
q.push_back(i);
if(i>=k-1) res.push_back(nums[q.front()]);//满了就开始push_back了
}
return res;
环形子数组最大和：维护的是前缀和一段的最值。
另外：看到环把他扯成2n长度的线。
int n=A.size();
for(int i=0;i<n;i++) A.push_back(A[i]);
vector<int> sum(n*2+1);
for(int i=1;i<=n*2;i++)
{
sum[i]=sum[i-1]+A[i-1];
}
int res=INI_MIN;
deque<int> q;
q.push_back(0);
for(int i=1;i<=n*2;i++)
{
if(q.size()&&i-n>q.front()) q.pop_front();
if(q.size()) res=max(res,sum[i]-sum[q.front()]);
while(q.size()&&sum[q.back()]>=sum[i]) q.pop_back();
q.push_back(i);
}
return res;
deque
双端队列deque是一个支持在两端高效率插入删除的vector。可以随机索引访问。也可以运用
begin,end,
front,back,
push_front,push_back,
pop_front,pop_back来对首尾进行高效率操作。
stack
操作： push/pop/top
运用：单调栈、对顶栈、前中后缀表达式、模拟递归、N项Catalan数 。
set
set最重要的作用就是去重了
包含set（有序去重）,multiset（有序多重）,unordered_set（无序去重）
set和multiset需要定义小于号。
在set中，迭代器遍历的顺序是从小到大的，s.begin()是指向最小元素的迭代器。–s.end()是指向最大元素的迭代器。
s.insert(x)
s.find(x): 找到第一个等于x的元素，返回迭代器。如果没有则返回s.end()
s.lower_bound(x)/s.upper_bound(x)
s.count(x)
s.erase(it) 删除迭代器指向的元素
s.erase(x) 删除所有等于x的元素
map
map的内部基于平衡树实现。
平衡树BST就是任何子树的左右子树高度相差最多为1。
让h维持在logn左右，时间复杂度比较小。
有时候BST也要手写，比如动态维护有多少个>=某个数的数，请自行思考。
有以下几种：
- 红黑树
- AVL
- SBT
- Treap(比较重要)
- 伸展树
举个栗子：用map统计字符串出现的次数
map<string,int> h;
char str[25];
for(int i=1;i<=n;i++)
{
cin>>str;
h[str]++;
}
for(int i=1;i<=m;i++)
{
cin>>str;
if(h.find(str)==h.end()) puts("0");
else cout<<h[str];
}
unordered_map和哈希
map和unordered_map都是做哈希操作的。
哈希是一种映射，把很多数映射到比较少的数上，就能节省时间空间了0v0
但是这不可避免会发生冲突，这时候有两种方式解决冲突：
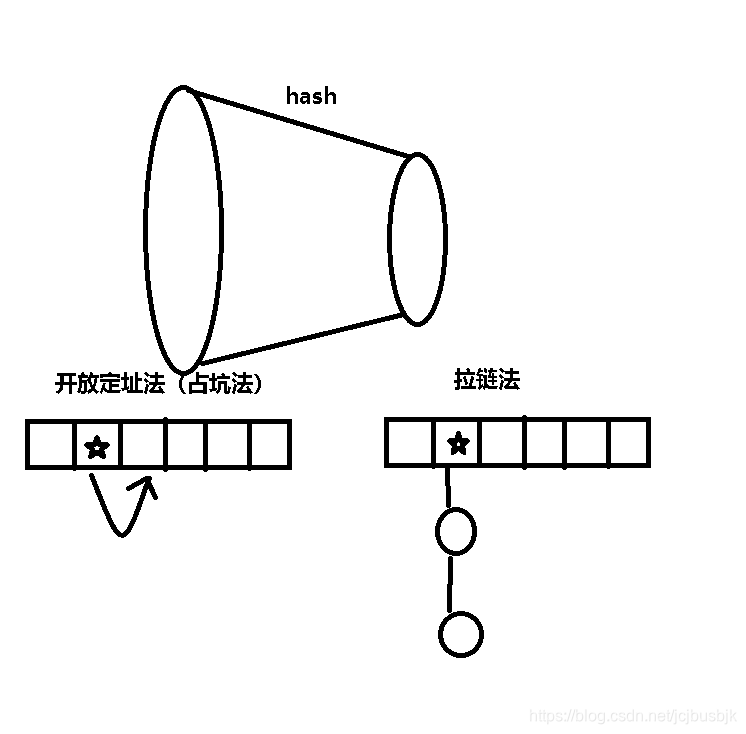
首先，一般来说我们取哈希表的大小都是数据大小两到三倍的质数。其次，不要映射成0，容易冲突。
开放定址：
int h[N];
int i=(x%N+N)%N;
while(h[i]!=Null&&h[i]!=x)
{
i++;
if(i==N)//找到末尾了
i=0;
}
return i;
拉链：
int h[N],e[N],ne[N],idx;//数组模拟邻接表
void insert(int x)
{
int k=(x%N+N)%N;
e[idx]=x;
ne[idx]=h[k];
h[k]=idx++;
}
bool find(int x)
{
int k=(x%N+N)%N;
for(int i=h[k];i!=-1;i=ne[i])
{
if(e[i]==x) return true;
}
return false;
}
上面是哈希表的实现方式，实际做题的时候我们用unordered_map就可以解决。
定义、查询和遍历操作
#include<unordered_,ap>
unordered_map<string,int>//key,value
hash["hello"]++;
//查询
if(hash.count("hello")!=0)
if(hash.find("hello"!=hash.end()))
//遍历
for(unordered_map<string,int>::iterator
it=hash.begin();it!=hash.end();it++)
如果是一个自定义的结构体（这里用了Acwing yxc博文的代码和讲解）：
(1) 哈希函数，需要实现一个class重载operator()，
就是你自定义的类型代表哪个数（size_t）？写一个这样的函数。
(2) 重载等于号。
代码：
#include <iostream>
#include <vector>
#include <unordered_map>
using namespace std;
class Myclass
{
public:
int first;
vector<int> second;
// 重载等号，判断两个Myclass类型的变量是否相等
bool operator== (const Myclass &other) const
{
return first == other.first && second == other.second;
}
};
// 实现Myclass类的hash函数
namespace std
{
template <>
struct hash<Myclass>
{
size_t operator()(const Myclass &k) const
{
int h = k.first;
for (auto x : k.second)
{
h ^= x;
}
return h;
}
};
}
int main()
{
unordered_map<Myclass, double> S;
Myclass a = { 2, {3, 4} };
Myclass b = { 3, {1, 2, 3, 4} };
S[a] = 2.5;
S[b] = 3.123;
cout << S[a] << ' ' << S[b] << endl;
return 0;
}
作者：yxc
链接：https://www.acwing.com/blog/content/9/
来源：AcWing
hash一般在题目数字比较庞大爆ull的时候使用。或者用来降低复杂度，避免重复遍历，就像查表一样O(1)插入和查询。
此外还有很多不在头文件的数据结构，在数据结构的博文中会进行详细的扩充。
容易错的
忘记 输入，==，忘记初始化，浮点数精度，一些语句放循环内还是循环外，数组开小了
一些边缘数据一定要记得考虑！0和1和2之类的！
前缀和与差分
前缀和用于求一个数组中，从l到r这一段的和。
动态维护前缀和请转到线段树和树状数组。
前缀最值
维护一个前缀的最值，实时比较实时操作。
例如下面这题：LC155
//min stack
void push(int x)
{
stk.push(x);
if(stk_min.empty()) stk_min.push(x);
else stk_min.push(min(x,stk_min.top()));
}
void pop()
{
stk.pop();
stk_min.pop();
}
int top()
{
return stk.top();
}
int getMin()
{
return stk_min.top();
}
双指针算法
双指针在leetcode里有很多题目都很好。
先想暴力怎么做，看看双指针能否优化（一般会具有某种单调性，让i和j之间相互约束从而减少复杂度）。
归并排序就是一个典型的双指针算法，这是用于对比两个数组的。值得一提的是，如果要放在原数组中建议倒序遍历。
unique函数的实现也是双指针算法，一个指针指向遍历到哪里，另一个指向数字放到哪里。
在排好序的数组中找出两数之和等于k，可以利用单调性，若是i1>i2必定有j1<j2，所以一个正序一个倒序遍历即可。
下面是两题比较有思考价值的：
最小覆盖子串问题
两个指针就像两个边界，维护一个窗口，开hash表统计T里面字母出现次数。
这里有个技巧，我们把目标的数值作为hash值，就能统一用hash[i]是否为0表示我们是否达到了要求。
如果多余了，前指针就往后指，达到目标的时候与res比较看是否更短，更新最小值。
unordered_map<char,int> hash;
for(auto c:t) hash[c]++;//我们需要的字母都变成1
int cnt=hash.size();
string res;
for(int i=0,j=0;i<s.size();i++)
{
if(hash[s[i]]==1) cnt++;
hash[s[i]]--;
while(hash[s[j]]<0)
{
hash[s[j++]]++;//如果重复了
}
if(c==cnt)//找到c个，比较找出最短的
{
if(!res.empty()||res.size()>i-j+1)
res=substr(j,i-j+1);
}
括号匹配问题
只要涉及括号的匹配，就会有个catlan数的性质出现。
设左括号为1，有括号为-1.
括号序列合法等价于所有前缀和大于等于0且总和等于0.
分cnt与零的关系分类讨论。
最后还要反过来做一遍。于是我们可以写一个函数做，这样不用写两遍，直接reverse原序列再做。
代码：
int work(string s)
{
int res=0;
for(int i=0,start=0,cnt=0;i<s.size();i++)
{
if(s[i]=='(') cnt++;
else
{
cnt--;
if(cnt<0) start=i+1,cnt=0;
else if(!cnt) res=max(res,i-start+1);
}
}
return res;
}
int longestValidParentheses(string s)
{
int res=work(s);
reverse(s.begin(),s.end());
for(auto &c:s) c^=1;//引用
return max(res,work(s));
}
高精度
高精度加法
思路：先把a和b倒序一下，如果哪个长就继续做和0的加法。
add中保存好进位，往vector中push当前位。
最后别忘了倒序回来。
#include<iostream>
#include<string>
#include<algorithm>
#include<vector>
using namespace std;
vector<int> v;
string a,b;
void add(char a,char b,int &next)
{
int sum=(a-'0')+b-'0'+next;
int local=sum%10;
v.push_back(local);
next=sum/10;
}
int main()
{
cin>>a>>b;
reverse(a.begin(),a.end());
reverse(b.begin(),b.end());
int i=0;
int next=0;
while(i<a.size()&&i<b.size())
{
add(a[i],b[i],next);
i++;
}
while(i<a.size())
{
add(a[i],'0',next);
i++;
}
while(i<b.size())
{
add('0',b[i],next);
i++;
}
if(next==1)
{
v.push_back(1);
}
reverse(v.begin(),v.end());
for(int j=0;j<v.size();j++)
{
cout<<v[j];
}
return 0;
}
高精度乘法
思路：保存进位，push当前位。如果最后还有进位也要push进去。
#include<iostream>
#include<vector>
#include<string>
#include<algorithm>
using namespace std;
vector<int> v;
string a;
int b;
void multi(string a,int b)
{
int t=0;
for(int i=0;i<a.size();i++)
{
t+=(a[i]-'0')*b;
v.push_back(t%10);
t/=10;
}
while(t)
{
v.push_back(t%10);
t/=10;
}
}
int main()
{
cin>>a>>b;
reverse(a.begin(),a.end());
multi(a,b);
reverse(v.begin(),v.end());
for(int i=0;i<v.size();i++)
{
cout<<v[i];
}
return 0;
}
高精度除法
思路：和列除法式子一样，余数乘10进行下一轮。
另：最后倒过来删除前导零。
#include<iostream>
#include<algorithm>
#include<string>
#include<vector>
using namespace std;
vector<int> v;
string a;
int b,r=0;
void div(string a,int b,int &r)
{
for(int i=0;i<a.size();i++)
{
r=r*10+a[i]-'0';
v.push_back(r/b);
r=r%b;
}
reverse(v.begin(),v.end());
while(v.size()>1&&v.back()==0)
{
v.pop_back();
}
}
int main()
{
cin>>a>>b;
div(a,b,r);
reverse(v.begin(),v.end());
for(int i=0;i<v.size();i++)
{
cout<<v[i];
}
cout<<endl<<r;
return 0;
}
二进制与倍增
这个仍然参考了《算法竞赛进阶指南》0v0
下面要讲的快速幂就是一种倍增技巧的应用。
背包问题中可以用倍增优化。
ST算法实现LCA也是倍增的应用。
倍增简而言之就是由于任何整数都可以表示若干个2的幂次和，我们用2的幂次和表示0~2k-1，只需要logK个代表值，大大降低了复杂度。
如果空间太大，线性递推没办法满足时间与空间复杂度要求，也可以用倍增进行优化。
【代码以后补充？】
快速幂
二分幂和快速幂的想法很相似，只不过不用二进制写，这里就不说了。当进行数的幂次运算时，复杂度由O(n)降低为O(logn)。
思路：枚举每一位，如果是1，则res*=a，如果不是1，就将a=a*a提升一位。
一般这种题都会越界要记得%mod
代码：
int quickpow(int a,int b)
{
int res=1;
while(b)
{
if(b&1)
{
res=res*a%mod;
}
a=a*a%mod;
b=b>>1;
}
return res;
}
矩阵快速幂同理，只不过初始化的时候是一个单位矩阵，并且乘的时候用一个函数实现矩阵乘法（矩阵用一个记录维度和内容的结构体存储）：
struct matrix {
int a[100][100];
int n;
};
matrix matrix_mul(matrix A, matrix B, int mod) {
matrix ret;
ret.n = A.n;
for (int i = 0; i < ret.n; i++) {
for (int j = 0; j < ret.n; j++){
ret.a[i][j] = 0;
}
}
for (int i = 0; i < ret.n; i++) {
for (int j = 0; j < ret.n; j++) {
for (int k = 0; k < A.n; k++) {
ret.a[i][j] = (ret.a[i][j] + A.a[i][k] * B.a[k][j] % mod) % mod;
}
}
}
return ret;
}
matrix unit(int n)
{
matrix ret;
ret.n=n;
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
if(i==j)
{
ret.a[i][j]=1;
}
else
{
ret.a[i][j]=0;
}
}
}
return ret;
}
matrix matrix_pow(matrix A,int p,int mod)
{
matrix res=unit(A.n);
for(;p;p/=2)
{
if(p&1)
{
res=matrix_mul(res,A,mod);
}
A=matrix_mul(A,A,mod);
}
return res;
}
单纯的矩阵乘法需要判断中间那一维是否能接上：
#include <iostream>
using namespace std;
struct matrix
{
int a[100][100];
int n,m;
};
matrix matrix_mul(matrix A,matrix B)
{
matrix ret;
ret.n=A.n;
ret.m=B.m;
for(int i=0;i<ret.n;i++)
{
for(int j=0;j<ret.m;j++)
{
ret.a[i][j]=0;
}
}
for(int i=0;i<ret.n;i++)
{
for(int j=0;j<ret.m;j++)
{
for(int k=0;k<A.m;k++)
{
ret.a[i][j]+=A.a[i][k]*B.a[k][j];
}
}
}
return ret;
}
int main() {
matrix A,B;
cin>>A.n>>A.m;
for(int i=0;i<A.n;i++){
for(int j=0;j<A.m;j++)
{
cin>>A.a[i][j];
}
}
cin>>B.n>>B.m;
for(int i=0;i<B.n;i++)
{
for(int j=0;j<B.m;j++)
{
cin>>B.a[i][j];
}
}
if(A.m!=B.n)
{
cout<<"No"<<endl;
}
else
{
matrix C=matrix_mul(A,B);
for(int i=0;i<C.n;i++)
{
for(int j=0;j<C.m;j++)
{
if(j!=C.m-1)
{
cout<<C.a[i][j]<<" ";
}
else
{
cout<<C.a[i][j]<<endl;
}
}
}
}
return 0;
}
动态规划中有一个经典题目，如何加括号让矩阵的连乘次数最少。
离散化
我们在讲STL的时候已经提到，用erase(unique(v.begin(),v.end()),v.end())这句话进行离散化。那么离散化的应用场景是什么呢？
一些数字，他们有着很大的范围，但是个数很少，并且这些数字大小本身不重要，只看他们之间的大小关系。
数量庞大的方块，他们之间有的有颜色，但大多没颜色。
一个超大的迷宫，空白的地方很多。
所以离散化的应用场景大家就自己意会吧。
【写到题目再更】
写太多了，其余寒假放到下篇讲。。。。
扫一扫
457
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
