剑指 Offer 53 - I. 在排序数组中查找数字 I（两次二分查找）

个人初始解法：二分查找+线性搜索

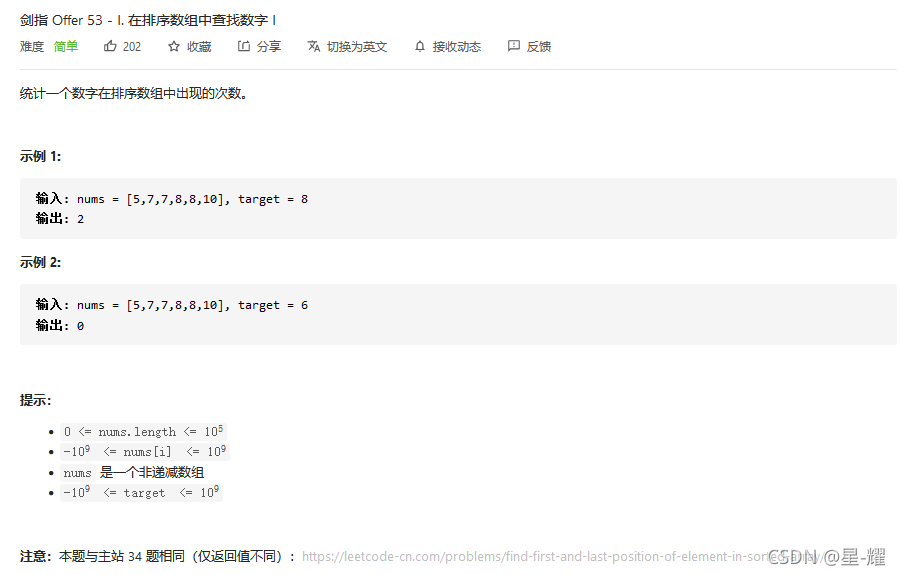
思路：通过二分查找定位到target位置，以此为起点，向两边线性搜索target并统计次数。

int binarySearch(int *nums, int left, int right, int target)
{
    while(left <= right)
    {
        int mid = left + (right-left)/2;
        if(nums[mid] == target) return mid;
        else if(nums[mid] < target) left = mid + 1;
        else right = mid - 1;
    }
    return -1;//查找失败
}

int search(int* nums, int numsSize, int target){
    int index = binarySearch(nums, 0, numsSize-1, target);
    // 没找到，次数为0
    if( index == -1) return 0;

    // 找到了，则向两边线性搜索，统计次数
    int ret = 1;
    // 向左线性搜索
    int p = index - 1;
    while(p >= 0)
    {
        if(nums[p] != target) break;
        ret++, p--;
    }
    //向右线性搜索
    int q = index + 1;
    while(q<numsSize)
    {
        if(nums[q] != target) break;
        ret++, q++;
    }
    return ret;
}

时间复杂度分析：当数组中全是相同元素时，该算法退化为线性查找，最坏时间复杂度$O(n)$;
空间复杂度$O(1)$。

官方解法：两次二分查找
思路：通过两次二分查找确定target的左、右边界位置，记为left和right，则target的个数为right-left+1。

怎么做？在原来的二分法基础上进行简单修改。
当查找左边界时，如果找到目标值，此时nums[mid]==target，还不能确定mid位置就是左边界。
先将现在的target位置用temp记录下来，然后继续在其左区间进行查找是否还有target。如果找到了新的target，就更新temp的值；如果没找到，则temp记录的位置就是左边界。
同理，当查找右边界时，用temp记录target的位置，但是接下来在其右区间进行查找，找到了就更新temp的值；没找到，则temp记录的位置就是右边界。
个人C版本，比官方更易理解：
bool从C99开始可以使用。

int binarySearch(int *nums, int numsSize, int target, bool lower)
{
    int left = 0, right = numsSize - 1;
    int temp  = -1;
    while(left <= right)
    {
        int mid = left + (right-left)/2;
        if(nums[mid] == target)
        {
            temp = mid;
            if(lower) right = mid - 1;
            else left = mid + 1;
        }
        else if(nums[mid] < target) left = mid + 1;
        else right = mid - 1;
    }
    return temp;//查找失败返回-1；查找成功返回索引值
}

int search(int* nums, int numsSize, int target){
    int left = binarySearch(nums, numsSize, target, true);
    int right = binarySearch(nums, numsSize, target, false);
    return left == -1 ? 0 : right - left + 1;
}

时间复杂度$O(logn)$：进行了两次二分查找
空间复杂度$O(1)$。