动态规划：打家劫舍

打家劫舍

题干：

给定一个nums[], nums[i]表示第i个房子里的资金，不能盗取相邻的两家否则会触发报警。求不触发报警情况下，最多可以盗取多少资金

nums = [2,7,9,3,1] // 答案：12

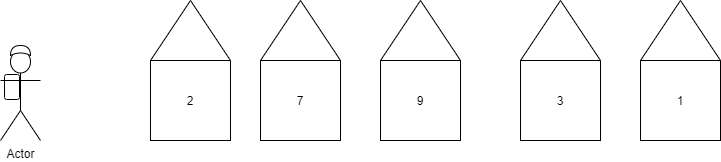
设计状态

定义最优状态数组dp=[],dp[i]表示不触发2报警情况下，打劫到第i家时盗取的最大资金。

解题思路

先算出局部最优解，用局部最优解递推出全局最优解。

步骤

当房子只有1间的时：

就直接盗取这间，dp[0]=nums[0] = 2

当房子有2间时：

不能盗取相邻的，因此二选一。

因此dp[1]=max(nums[0],nums[1])=max(2,7)=7

当房子有3间时：

不能盗取相邻的，前面已算出盗取1间和两间的最优解。不能盗取相邻的，所以3间有2种情况：

1. 至第1间为止的最大获利+盗取第3间，最大收获为：dp[0]+nums[2]
2. 至第2间为止的最大获利。最大收获为：dp[1]

最终，盗取3间最大获利为： dp[2] = max(dp[0]+nums[2],dp[1]) = max(11,7)=11

当房子有n间时：

当要求盗取第n间的最大获利时，前面我们已经算出了盗取至n-1和n-2的最大获利。那么此时有两种情况：

1. 盗取第n间。就只能获得前面至n-2间的最大获利，因为相邻的n-1不能盗取,最终获利为：dp[n-2]+nums[n]

2. 不盗取第n间。那么最大获利就是，前面算出的至前上一间房子为止的最大获利：dp[n-1]

最终，盗取n间的最大获利为：dp[n]=max(dp[n-2]+nums[n],dp[n-1])

代码编写（用js）

function  houseRobbery(){
    nums = [2,7,9,3,1] // 答案：12
    // 定义初始状态 dp[i] 表示打劫到第i家为止最大的资金
    dp = [nums[0]]
    // 状态转移方程： dp[i] = max(dp[i-1],dp[i-1]+nums[i])
    for(let i=1;i<nums.length;i++){
        if(i==1){
            dp[i] = max(dp[i], nums[i])
        }else{
            dp[i] = max(dp[i-1], dp[i-2]+nums[i])
        }
    }
    return "最大盗取获利为："+dp[nums.length-1]+"\n"

}
/*
结果： 最大盗取获利为：12
*/
function max(a,b){
    return a > b ? a : b
}

总结：

动态规划的解题思路就是化大问题为小问题，通过局部最优解推出全局最优解。先求出1个元素时的最优解，通过第一个最优解去推出2个元素时的最优解，通过第二个最优解继续推出3个元素时的最优解。直到第n个。

此类问题为线性问题，处理起来还算简单。下一次开始将研究多维的问题的解法。

至于下次更新在什么时候。看看下周吧