LeetCode 886 Possible Bipartition

题目

Given a set of N people (numbered 1, 2, …, N), we would like to split everyone into two groups of any size.
Each person may dislike some other people, and they should not go into the same group.
Formally, if dislikes[i] = [a, b], it means it is not allowed to put the people numbered a and b into the same group.
Return true if and only if it is possible to split everyone into two groups in this way.
Example 1:
Input: N = 4, dislikes = [[1,2],[1,3],[2,4]]
Output: true
Explanation: group1 [1,4], group2 [2,3]
Example 2:
Input: N = 3, dislikes = [[1,2],[1,3],[2,3]]
Output: false
Example 3:
Input: N = 5, dislikes = [[1,2],[2,3],[3,4],[4,5],[1,5]]
Output: false
Note:
1 <= N <= 2000
0 <= dislikes.length <= 10000
1 <= dislikes[i][j] <= N
dislikes[i][0] < dislikes[i][1]
There does not exist i != j for which dislikes[i] == dislikes[j].

思路

这道题可以采用图染色算法。具体思路是首先根据题目给出的条件构造图。每个节点代表一个人，如果存在dislike的关系，用边表示，一条边代表相连的这两个节点是dislike的。构造完图之后，给每个节点染色，把节点染成两种颜色，如果完成整个图的染色不出现错误，那么就说这个图是可以二分的。染色规则是这样的：

每个节点的颜色都要跟相邻节点的颜色不同，每个节点都染上颜色才能说这个图完成了染色。

为了更好理解，我画出了Example1 和 Example3 的示意图：

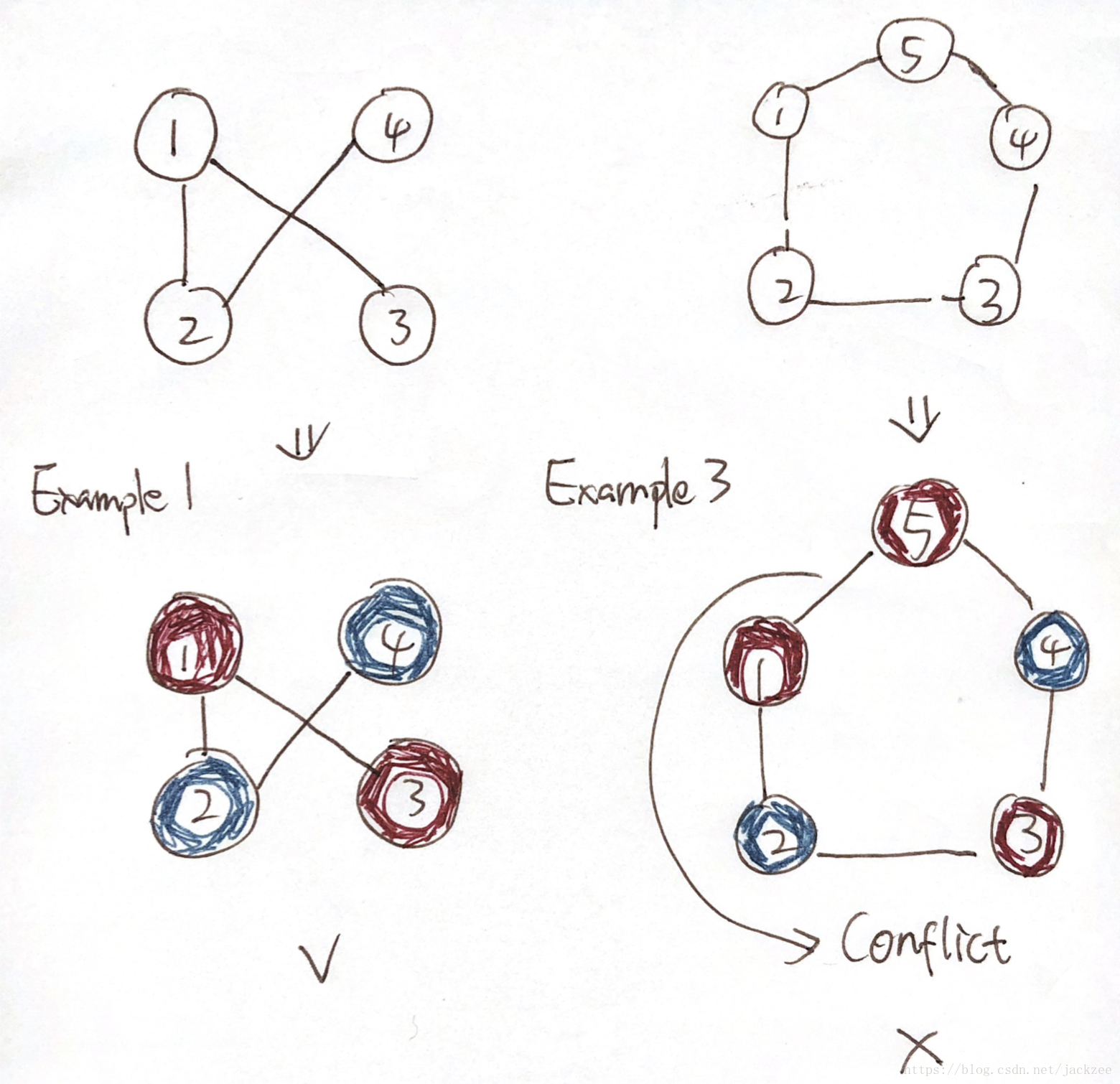
因此，解决这个问题的思路很简单，第一步构造图，第二部染色。

代码实现

构造图

首先要选择一种数据结构来存储图。可以用HashMap，key是Integer类型，代表节点的具体数字，value存放一个数组，数组里面存放的也是Integer，用来表示与当前节点存在dislike关系的节点。也可以理解为，key是节点，value是与这个节点相连的所有的边，这样就可以存储一张图了。

染色

染色这个过程，首先需要一个数组来存储每个节点的颜色。为了逻辑上更加清晰，数组大小定位N-1，下表和点的编号就可以一一对应。然后编写一个染色方法，接收两个关键的参数，要染色的点的编号，以及要染成的颜色，返回一个布尔值，代表能否染色成功。从下标为1的元素开始遍历颜色数组，一旦发现这个节点在图里面有边与其相连，就开始染色（如果这个点是孤立的，最后放在哪一组也不影响，可以直接跳过）。而染色方法内部会进行递归，如果全部染色成功，说明这个图是二分的。

代码：

public class LeetCode886 {

    //define a hashMap used to store the graph
    Map<Integer, ArrayList<Integer>> graph = new HashMap<>();
    
    public boolean possibleBipartition(int N, int[][] dislikes) {
        for (int[] dis : dislikes) {
            //store the dislike relations in the ArrayList,which is the edges of the map
            if (!graph.containsKey(dis[0])) graph.put(dis[0], new ArrayList<>());
            graph.get(dis[0]).add(dis[1]);
            if (!graph.containsKey(dis[1])) graph.put(dis[1], new ArrayList<>());
            graph.get(dis[1]).add(dis[0]);
        }
        //the array used to store the colors of each vertex(0 for default, 1 for red, -1for blue)
        int[] colors = new int[N + 1];
        for (int i = 1; i <= N; i++) {
            if (graph.get(i) == null) continue;
            if (colors[i] == 0 && !paint(i, colors, 1))
                return false;
        }
        return true;
    }

    //return if it can successfully paint this vertex with color
    public boolean paint(int index, int[] colors, int color) {
        if (colors[index] != 0)
            return colors[index] == color;
        colors[index] = color;
        int length = graph.get(index).size();
        for (int i = 0; i < length; i++) {
            if (!paint(graph.get(index).get(i), colors, -1 * color))
                return false;
        }
        return true;
    }
}