牛客多校-1-H Hash Function (NTT加速)

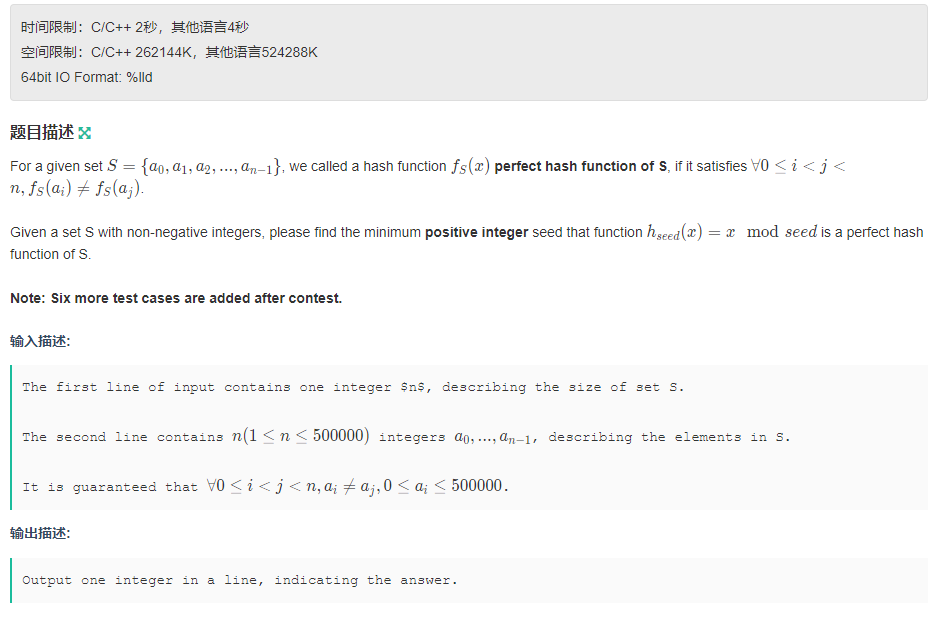
题目

样例

Input

3
2 3 4

Output

3

Input:

10
0 7 23 18 29 27 6 28 24 11Input

Output:

15

题意：给一个整数集 P，求一个最小的整数 sedd 使得 P 中的数对 seed 取模所得互不相同。

思路

• 可以将题目转化为求seed，使得对任意不同的 i,j， (p[i]-p[j]) % seed != 0。
• 若差值只取正数，那么所能得到的值只能是 0..500000 中的数。要是能对 1,,500000 的所有数知道它是否是一个差值，那么从小到大枚举最终答案 ans，再枚举 k 取遍 0..500000 中 ans 的倍数，验证是否是差值即可。
• 令 A=500000 这样的时间复杂度是
  $$\frac{A}{1}+\frac{A}{2}+\frac{A}{3}+...+\frac{A}{A}=O(A)$$
• 下面就是如何快速得到差值的集合。
• 构造两个多项式 ( a[i]=(i在集合P中) ? 1 : 0) (为了书写简便，令 N=n-1 )
  F(x) = a[0] + a[1] x + a[2] x^2 + a[3] x^3 + ... + a[N] x^N
G(x) = a[N] + a[N-1]x + a[N-2] x^2 +