D. Contact ATC

最新推荐文章于 2021-09-06 10:14:39 发布

原创最新推荐文章于 2021-09-06 10:14:39 发布 · 1.9k 阅读

0 ·

CC 4.0 BY-SA版权

数据结构与算法专栏收录该内容

63 篇文章

订阅专栏

本文探讨了一个有趣的问题：在有风的情况下，多架飞机如何能够同时到达原点。通过分析飞机到达时间与风速的关系，利用数据结构进行高效计算，提出了两种解决方案。

D. Contact ATC
time limit per test1 second
memory limit per test256 megabytes
inputstandard input
outputstandard output
Arkady the air traffic controller is now working with n planes in the air. All planes move along a straight coordinate axis with Arkady’s station being at point 0 on it. The i-th plane, small enough to be represented by a point, currently has a coordinate of xi and is moving with speed vi. It’s guaranteed that xi·vi < 0, i.e., all planes are moving towards the station.

Occasionally, the planes are affected by winds. With a wind of speed vwind (not necessarily positive or integral), the speed of the i-th plane becomes vi + vwind.

According to weather report, the current wind has a steady speed falling inside the range [ - w, w] (inclusive), but the exact value cannot be measured accurately since this value is rather small — smaller than the absolute value of speed of any plane.

Each plane should contact Arkady at the exact moment it passes above his station. And you are to help Arkady count the number of pairs of planes (i, j) (i < j) there are such that there is a possible value of wind speed, under which planes i and j contact Arkady at the same moment. This value needn’t be the same across different pairs.

The wind speed is the same for all planes. You may assume that the wind has a steady speed and lasts arbitrarily long.

Input
The first line contains two integers n and w (1 ≤ n ≤ 100 000, 0 ≤ w < 105) — the number of planes and the maximum wind speed.

The i-th of the next n lines contains two integers xi and vi (1 ≤ |xi| ≤ 105, w + 1 ≤ |vi| ≤ 105, xi·vi < 0) — the initial position and speed of the i-th plane.

Planes are pairwise distinct, that is, no pair of (i, j) (i < j) exists such that both xi = xj and vi = vj.

Output
Output a single integer — the number of unordered pairs of planes that can contact Arkady at the same moment.

Examples
inputCopy
5 1
-3 2
-3 3
-1 2
1 -3
3 -5
output
3
inputCopy
6 1
-3 2
-2 2
-1 2
1 -2
2 -2
3 -2
output
9
Note
In the first example, the following 3 pairs of planes satisfy the requirements:

(2, 5) passes the station at time 3 / 4 with vwind = 1;
(3, 4) passes the station at time 2 / 5 with vwind = 1 / 2;
(3, 5) passes the station at time 4 / 7 with vwind = - 1 / 4.
In the second example, each of the 3 planes with negative coordinates can form a valid pair with each of the other 3, totaling 9 pairs.

题意是，在一个有正负的一维坐标轴上有若干飞机。每辆飞机在初始的坐标，并且有飞行的速度。
现在有风，并且风的速度的最大值一定，为w，然后并且风的最大速度没有其中任何一辆飞机的速度大。
现在问你有多少不同对飞机，在某个风速的情况下能够同时到达原点。
很显然，每个飞机到达的时间为abs(index / v +或者- w)这个区间内的任意值
那么要判断两辆飞机能否同时到达，应该是看到达的时间是否有交点。

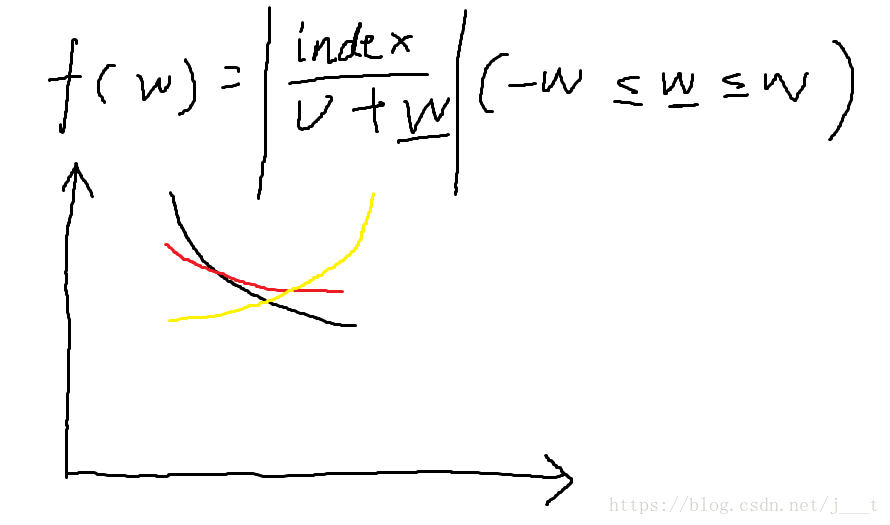
如上图所示，这个函数一定是单调的，如果要求得一个w使得两个f(w)相等，那么必然是这两个飞机的函数有交点。
有交点是什么意思呢？是两个飞机到达时间的区间相交吗？
不，请看下面这个例子。
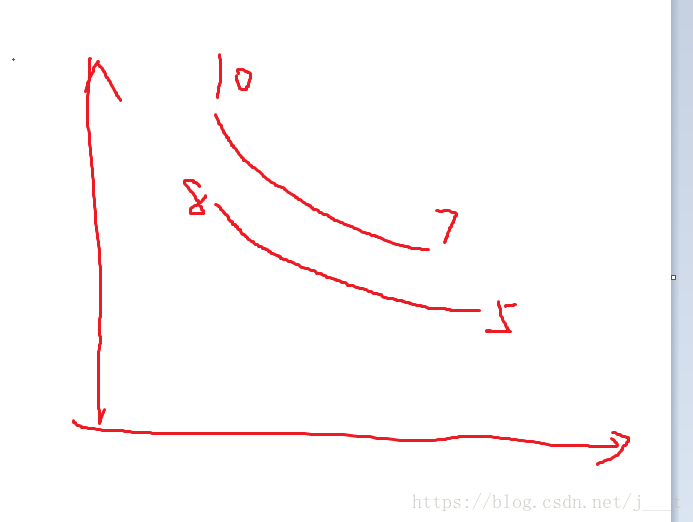
这里写图片描述
两个区间是【5，8】和【7，10】，但是并没有一个w能够使得他们相交，也就是同时到达原点。
那么看我第一个图，两个函数图像相交的根本因素，在于它们左端点的序列和右端点的序列相对顺序（也就是偏序）不一样。
也就是在-w的时候他们的顺序和w的时候顺序不一样！
OK那也就是我先按-w的情况sort一下，按w的情况sort一下，看看同一个飞机在两次排序中的次序是否相同。
那么如何在nlogn的时间内求不同次序呢？
可以用BIT或者线段树来做。（由于我不会BIT，下面就是用线段树模板写的。）
反正原理就是，按右端点sort之后的顺序来检索，每加入一个点（单点更新），看看之前有几个飞机的顺序（左端点sort的顺序）本来该在它之后的，却在它之前就出现过（区间查询）。
然后这样就可以求出来所有的逆序对了。

当然仅仅如此还是不行的，为什么呢？看下图：
这里写图片描述
如果两辆飞机的左端点或者右端点时间是一样的，那么我们的sort是无法保证在sort序列里他们的相对顺序的，但是这种情况我们是一定要让res+1的。

个人猜测，两条函数图像的增长速度在w改变很小的情况下，应该是不变的。
所以我们把w的范围+一个很小的数，这样他们的左端点次序和右端点次序就不会一样了。
就能符合我们用顺序来求res的方法了。
但这个加上去的数也不能很大，因为搞不好左端点两个相近的数被你这么一弄，变成次序相反了。
所以这个数要尽可能的小。
下面是AC代码：

#include <bits/stdc++.h>
#define N (int)1e5+10
typedef long long ll;
using namespace std;
struct node{
	int id;
	double index, v;
	bool operator< (const node& b) const{
		return fabs(index * b.v) < fabs(b.index * v);
	}
}arr[N];
int a[N], b[N];
#define lc root<<1
#define rc root<<1|1
struct seg{
	int l, r;
	ll he, lazy, tag;
}t[N<<2];
void build(int root, int l, int r)
{
	t[root].l = l, t[root].r = r;
	t[root].lazy = 0;
	t[root].tag = -1;
	if (l == r)
	{
		t[root].he = 0;
		return;
	}
	int m = (l + r) >> 1;
	build(lc, l, m);
	build(rc, m+1, r);
	t[root].he = t[lc].he + t[rc].he;
}
void imptag(int root, ll change)
{
	t[root].tag = change;
	t[root].he = (t[root].r - t[root].l + 1) * change;
	t[root].lazy = 0;
}
void implazy(int root, ll change)
{
	t[root].lazy += change;
	t[root].he += (t[root].r - t[root].l + 1) * change;
}
void pushdown(int root)
{
	ll temp1 = t[root].tag;
	if (temp1 != -1)
	{
		imptag(lc, temp1);
		imptag(rc, temp1);
		t[root].tag = -1;
	}
	ll temp2 = t[root].lazy;
	if (temp2)
	{
		implazy(lc, temp2);
		implazy(rc, temp2);
		t[root].lazy = 0;
	}
}
void assignment(int root, int l, int r, ll change)
{
	if (r < t[root].l || l > t[root].r) return;
	if (l <= t[root].l && t[root].r <= r)
	{
		imptag(root, change);
		return;
	}
	pushdown(root);
	assignment(rc, l, r, change);
	assignment(lc, l, r, change);
	t[root].he = t[lc].he + t[rc].he;
}
void update(int root, int l, int r, ll change)
{
	if (r < t[root].l || l > t[root].r) return;
	if (l <= t[root].l && t[root].r <= r)
	{
		implazy(root, change);
		return;
	}
	pushdown(root);
	update(rc, l, r, change);
	update(lc, l, r, change);
	t[root].he = t[lc].he + t[rc].he;
}
ll query(int root, int l, int r)
{
	if (r < t[root].l || l > t[root].r) return 0;
	if (l <= t[root].l && t[root].r <= r)
	{
		return t[root].he;
	}
	pushdown(root);
	return query(rc, l, r) + query(lc, l, r);
}
int main(void)
{
	int n;
	double w;
	scanf("%d%lf", &n, &w);
	int i;
	w += 1e-6;
	for (i = 0; i < n; i++)
	{
		double a, b;
		scanf("%lf%lf", &a, &b);
		arr[i].index = a, arr[i].v = b - w;
	}
	sort(arr, arr+n);
	for (i = 0; i < n; i++)
	{
		a[i] = arr[i].id = i;
		arr[i].v += 2 * w;
	}
	sort(arr, arr+n);
	for (i = 0; i < n; i++)
	{
		b[i] = arr[i].id;
	}
	build(1, 0, n - 1);
	ll res = 0;
	for (i = 0; i < n; i++)
	{
		res += query(1, b[i]+1, n-1);
		update(1, b[i], b[i], 1);
	}
	printf("%lld", res);
}

当然，这种做法很有风险，因为你不知道w这个东西取多少是好的，有可能要WA好多发才测出来。
下面是一种稳妥的做法：
常规的逆序对定义是i < j, arr[i] > arr[j]，那我现在按左端点排序，并除去重复的那些值，然后再按右端点排序。
如果当前点i < j, arr[i] >= arr[j]，结果就加1。
代码如下：

#include <bits/stdc++.h>
#define N (int)1e5+10
typedef long long ll;
using namespace std;
struct node{
    int id;
    double index, v;
    node():id(0){}
    bool operator< (const node& b) const{
        return fabs(index * b.v) == fabs(b.index * v) ? id > b.id : fabs(index * b.v) < fabs(b.index * v);
    }
    bool operator== (const node& b) const{
        return fabs(index * b.v) == fabs(b.index * v);
    }
}arr[N], sup[N];
int a[N], b[N];
#define lc root<<1
#define rc root<<1|1
struct seg{
    int l, r;
    ll he, lazy, tag;
}t[N<<2];
void build(int root, int l, int r)
{
    t[root].l = l, t[root].r = r;
    t[root].lazy = 0;
    t[root].tag = -1;
    if (l == r)
    {
        t[root].he = 0;
        return;
    }
    int m = (l + r) >> 1;
    build(lc, l, m);
    build(rc, m+1, r);
    t[root].he = t[lc].he + t[rc].he;
}
void imptag(int root, ll change)
{
    t[root].tag = change;
    t[root].he = (t[root].r - t[root].l + 1) * change;
    t[root].lazy = 0;
}
void implazy(int root, ll change)
{
    t[root].lazy += change;
    t[root].he += (t[root].r - t[root].l + 1) * change;
}
void pushdown(int root)
{
    ll temp1 = t[root].tag;
    if (temp1 != -1)
    {
        imptag(lc, temp1);
        imptag(rc, temp1);
        t[root].tag = -1;
    }
    ll temp2 = t[root].lazy;
    if (temp2)
    {
        implazy(lc, temp2);
        implazy(rc, temp2);
        t[root].lazy = 0;
    }
}
void assignment(int root, int l, int r, ll change)
{
    if (r < t[root].l || l > t[root].r) return;
    if (l <= t[root].l && t[root].r <= r)
    {
        imptag(root, change);
        return;
    }
    pushdown(root);
    assignment(rc, l, r, change);
    assignment(lc, l, r, change);
    t[root].he = t[lc].he + t[rc].he;
}
void update(int root, int l, int r, ll change)
{
    if (r < t[root].l || l > t[root].r) return;
    if (l <= t[root].l && t[root].r <= r)
    {
        implazy(root, change);
        return;
    }
    pushdown(root);
    update(rc, l, r, change);
    update(lc, l, r, change);
    t[root].he = t[lc].he + t[rc].he;
}
ll query(int root, int l, int r)
{
    if (r < t[root].l || l > t[root].r) return 0;
    if (l <= t[root].l && t[root].r <= r)
    {
        return t[root].he;
    }
    pushdown(root);
    return query(rc, l, r) + query(lc, l, r);
}
int main(void)
{
    int n;
    double w;
    scanf("%d%lf", &n, &w);
    int i;
    for (i = 0; i < n; i++)
    {
        double a, b;
        scanf("%lf%lf", &a, &b);
        arr[i].index = a, arr[i].v = b - w;
        sup[i] = arr[i];
    }
    sort(sup, sup+n);
    int m = unique(sup, sup+n)- sup;
    for (i = 0; i < n; i++)
    {
        arr[i].id = lower_bound(sup, sup+m, arr[i]) - sup;
        arr[i].v += 2 * w;
    }
    sort(arr, arr+n);
    for (i = 0; i < n; i++)
    {
        b[i] = arr[i].id;
    }
    build(1, 0, m - 1);
    ll res = 0;
    for (i = 0; i < n; i++)
    {
        res += query(1, b[i], m-1);
        update(1, b[i], b[i], 1);
    }
    printf("%lld", res);
}