双边滤波器（bilateral filter）

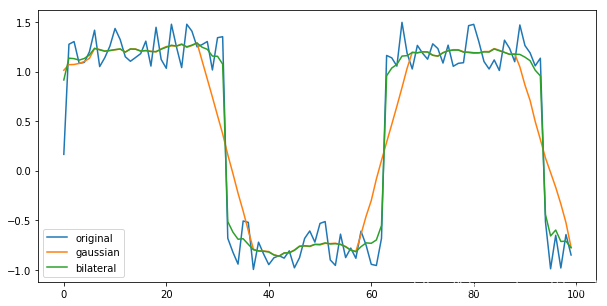
直接看看滤波结果吧，蓝线为原始信号，黄线为高斯滤波结果，绿线为双边滤波结果。

高斯滤波大家应该都很熟悉：
$$y_i^{\prime }=\sum _{j=i-H}^{i+H}{w}_{ij}{y}_j$$$$w_{ij}=\frac{1}{Z}\exp (-|i-j{|}^2/2{\sigma }^2)$$

滤波后每个点的信号值是其周边值得加权平均，权值仅仅由时空距离决定。

这样的弊端是什么呢？在处理阶跃信号的时候，很容易将信号的突变平滑掉。表现在图像处理上就是在去噪的同时，减损边缘信息。

双边滤波为什么可以保留边缘信息呢？

原因在于双边滤波的权值不仅仅取决于下标的时空距离，还取决与信号值之间的距离：
$$w_{ij}=\frac{1}{Z}\exp (-|i-j{|}^2/2{\sigma }_1^2)\exp (-|y_i-y_j{|}^2/2{\sigma }_2^2)$$

如果信号发生阶跃，比如某点右端的信号值普遍大于当前值，而左端的值则普遍接近，那么滤波时该点左端的权重会大于右端的权重，因而不会使得阶跃信号被平滑。

code

import math
import numpy as np
import matplotlib.pyplot as plt

def denoise_step(sample, H=3, dn1=1., dn2=1.):
    def get_denoise_value(idx):
        start_idx, end_idx = get_neighbor_idx(len(sample), idx, H)
        idxs = np.arange(start_idx, end_idx)
        weight_sample = sample[idxs]

        weights = np.array(list(map(lambda j: bilateral_filter(j, idx, sample[j], sample[idx], dn1, dn2), idxs)))
        return np.sum(weight_sample * weights)/np.sum(weights)

    idx_list = np.arange(len(sample))
    denoise_sample = np.array(list(map(get_denoise_value, idx_list)))
    return denoise_sample

def get_neighbor_idx(total_len, target_idx, H=3):
    '''
    Let i = target_idx.
    Then, return i-H, ..., i, ..., i+H, (i+H+1)
    '''
    return [np.max([0, target_idx-H]), np.min([total_len, target_idx+H+1])]

def gen_wave():
    N = 100
    t = np.linspace(0,10,N)
    y = np.sign(np.sin(t))
    y += np.random.random((N))*0.5
    return y

ts = gen_wave()

plt.figure(figsize=(10,5))
plt.plot(ts, label='original')

def bilateral_filter(j, t, y_j, y_t, delta1=1.0, delta2=1.0):
    idx1 = -1.0 * (math.fabs(j-t) **2.0)/(2.0*delta1**2)
    idx2 = 0  												# gaussian filter
    weight = (math.exp(idx1)*math.exp(idx2))
    return weight

ts1 = denoise_step(ts, H=5, dn1=10, dn2=1)
plt.plot(ts1, label='gaussian')

def bilateral_filter(j, t, y_j, y_t, delta1=1.0, delta2=1.0):
    idx1 = -1.0 * (math.fabs(j-t) **2.0)/(2.0*delta1**2)
    idx2 = -1.0 * (math.fabs(y_j-y_t) **2.0)/(2.0*delta2**2)
    weight = (math.exp(idx1)*math.exp(idx2))
    return weight

ts1 = denoise_step(ts, H=5, dn1=10, dn2=1)
plt.plot(ts1, label='bilateral')
plt.legend()
plt.show()