function solve_coupled_dde_with_history
% 固定延迟参数
tau = 1;
% 设置求解器选项
opts = ddeset('RelTol', 1e-8, 'AbsTol', 1e-10, 'MaxStep', 0.05);
% 时间范围 [0, 20]
tspan = [0, 20];
% ================== 求解主系统 ================== %
% 主系统历史函数 (t ∈ [-1, 0])
history_master = @(t) [...
1.3; % κ1^R
1.1; % κ1^I
3.0; % w1^R
-1.8; % w1^I
-2.0; % κ2^R
-1.2; % κ2^I
-1.0; % w2^R
1.3 % w2^I
];
fprintf('Solving Master System...\n');
tic;
sol_master = dde23(@master_ddefun, tau, history_master, tspan, opts);
toc;
% ================== 求解从系统 ================== %
% 从系统历史函数 (t ∈ [-1, 0])
history_slave = @(t) [...
1.8; % λ1^R
1.7; % λ1^I
3.9; % v1^R
0.3; % v1^I
-2.5; % λ2^R
-1.4; % λ2^I
-4.3; % v2^R
-0.4 % v2^I
];
fprintf('\nSolving Slave System...\n');
tic;
sol_slave = dde23(@slave_ddefun, tau, history_slave, tspan, opts);
toc;
% ================== 绘制结果 ================== %
plot_results(sol_master, sol_slave);
% ================== 同步误差分析 ================== %
analyze_synchronization(sol_master, sol_slave);
end
function dydt = master_ddefun(t, y, Z)
% 主系统状态变量分配:
% y(1) = κ1^R, y(2) = κ1^I, y(3) = w1^R, y(4) = w1^I
% y(5) = κ2^R, y(6) = κ2^I, y(7) = w2^R, y(8) = w2^I
% 延迟状态 (t - tau)
y_d = Z;
% 节点1的方程
dydt = zeros(8,1);
dydt(1) = -y(1) + y(3); % dot{κ}_1^R
dydt(2) = -y(2) + y(4); % dot{κ}_1^I
% w1^R方程中的min/max项
A1 = 0.4*tanh(y_d(1)) + 1.0*tanh(y_d(2));
B1 = -2.0*tanh(y_d(5)) + 0.3*tanh(y_d(6));
min1 = min(A1, B1);
C1 = 0.2*tanh(y_d(1)) + 2.5*tanh(y_d(2));
D1 = 2.0*tanh(y_d(5)) + 1.4*tanh(y_d(6));
max1 = max(C1, D1);
dydt(3) = -y(3) - 0.4*y(1) + 1.5*tanh(y(1)) - 2.6*tanh(y(2)) ...
- 2.0*tanh(y(5)) - 1.7*tanh(y(6)) ...
+ 2.5*tanh(y_d(1)) - 1.5*tanh(y_d(2)) ...
+ 1.0*tanh(y_d(5)) + 1.2*tanh(y_d(6)) ...
+ min1 + max1 + 2; % dot{w}_1^R
% w1^I方程中的min/max项
A2 = -1.0*tanh(y_d(1)) + 0.4*tanh(y_d(2));
B2 = -0.3*tanh(y_d(5)) - 2.0*tanh(y_d(6));
min2 = min(A2, B2);
C2 = -2.5*tanh(y_d(1)) + 0.2*tanh(y_d(2));
D2 = -1.4*tanh(y_d(5)) + 2.0*tanh(y_d(6));
max2 = max(C2, D2);
dydt(4) = -y(4) - 0.4*y(2) + 2.6*tanh(y(1)) + 1.5*tanh(y(2)) ...
+ 1.7*tanh(y(5)) - 2.0*tanh(y(6)) ...
+ 1.5*tanh(y_d(1)) + 2.5*tanh(y_d(2)) ...
- 1.2*tanh(y_d(5)) + 1.0*tanh(y_d(6)) ...
+ min2 + max2; % dot{w}_1^I
% 节点2的方程
dydt(5) = -y(5) + y(7); % dot{κ}_2^R
dydt(6) = -y(6) + y(8); % dot{κ}_2^I
% w2^R方程中的min/max项
A3 = 1.5*tanh(y_d(1)) + 1.6*tanh(y_d(2));
B3 = 1.1*tanh(y_d(5)) + 1.6*tanh(y_d(6));
min3 = min(A3, B3);
C3 = 0.5*tanh(y_d(1)) + 1.6*tanh(y_d(2));
D3 = 2.8*tanh(y_d(5)) - 0.6*tanh(y_d(6));
max3 = max(C3, D3);
dydt(7) = -0.4*y(7) - 1.6*y(5) + 1.2*tanh(y(1)) - 0.6*tanh(y(2)) ...
+ 1.0*tanh(y(5)) + 1.5*tanh(y(6)) ...
- 1.7*tanh(y_d(1)) + 2.7*tanh(y_d(2)) ...
- 2.4*tanh(y_d(5)) + 1.6*tanh(y_d(6)) ...
+ min3 + max3 + 2; % dot{w}_2^R
% w2^I方程中的min/max项
A4 = -1.6*tanh(y_d(1)) + 1.5*tanh(y_d(2));
B4 = -1.6*tanh(y_d(5)) + 1.1*tanh(y_d(6));
min4 = min(A4, B4);
C4 = -1.6*tanh(y_d(1)) + 0.5*tanh(y_d(2));
D4 = 0.6*tanh(y_d(5)) + 2.8*tanh(y_d(6));
max4 = max(C4, D4);
dydt(8) = -0.4*y(8) - 1.6*y(6) + 0.6*tanh(y(1)) + 1.2*tanh(y(2)) ...
- 1.5*tanh(y(5)) + 1.0*tanh(y(6)) ...
- 2.7*tanh(y_d(1)) - 1.7*tanh(y_d(2)) ...
- 1.6*tanh(y_d(5)) - 2.4*tanh(y_d(6)) ...
+ min4 + max4; % dot{w}_2^I
end
function dydt = slave_ddefun(t, y, Z)
% 从系统状态变量分配:
% y(1) = λ1^R, y(2) = λ1^I, y(3) = v1^R, y(4) = v1^I
% y(5) = λ2^R, y(6) = λ2^I, y(7) = v2^R, y(8) = v2^I
% 延迟状态 (t - tau)
y_d = Z;
% 节点1的方程
dydt = zeros(8,1);
dydt(1) = -y(1) + y(3); % dot{λ}_1^R
dydt(2) = -y(2) + y(4); % dot{λ}_1^I
% v1^R方程中的min/max项
A1 = 0.4*tanh(y_d(1)) + 1.0*tanh(y_d(2));
B1 = -2.0*tanh(y_d(5)) + 0.3*tanh(y_d(6));
min1 = min(A1, B1);
C1 = 0.2*tanh(y_d(1)) + 2.5*tanh(y_d(2));
D1 = 2.0*tanh(y_d(5)) + 1.4*tanh(y_d(6));
max1 = max(C1, D1);
dydt(3) = -y(3) - 0.4*y(1) + 1.5*tanh(y(1)) - 2.6*tanh(y(2)) ...
- 2.0*tanh(y(5)) - 1.7*tanh(y(6)) ...
+ 2.5*tanh(y_d(1)) - 1.5*tanh(y_d(2)) ...
+ 1.0*tanh(y_d(5)) + 1.2*tanh(y_d(6)) ...
+ min1 + max1 + 2; % dot{v}_1^R
% v1^I方程中的min/max项
A2 = -1.0*tanh(y_d(1)) + 0.4*tanh(y_d(2));
B2 = -0.3*tanh(y_d(5)) - 2.0*tanh(y_d(6));
min2 = min(A2, B2);
C2 = -2.5*tanh(y_d(1)) + 0.2*tanh(y_d(2));
D2 = -1.4*tanh(y_d(5)) + 2.0*tanh(y_d(6));
max2 = max(C2, D2);
dydt(4) = -y(4) - 0.4*y(2) + 2.6*tanh(y(1)) + 1.5*tanh(y(2)) ...
+ 1.7*tanh(y(5)) - 2.0*tanh(y(6)) ...
+ 1.5*tanh(y_d(1)) + 2.5*tanh(y_d(2)) ...
- 1.2*tanh(y_d(5)) + 1.0*tanh(y_d(6)) ...
+ min2 + max2; % dot{v}_1^I
% 节点2的方程
dydt(5) = -y(5) + y(7); % dot{λ}_2^R
dydt(6) = -y(6) + y(8); % dot{λ}_2^I
% v2^R方程中的min/max项
A3 = 1.5*tanh(y_d(1)) + 1.6*tanh(y_d(2));
B3 = 1.1*tanh(y_d(5)) + 1.6*tanh(y_d(6));
min3 = min(A3, B3);
C3 = 0.5*tanh(y_d(1)) + 1.6*tanh(y_d(2));
D3 = 2.8*tanh(y_d(5)) - 0.6*tanh(y_d(6));
max3 = max(C3, D3);
dydt(7) = -0.4*y(7) - 1.6*y(5) + 1.2*tanh(y(1)) - 0.6*tanh(y(2)) ...
+ 1.0*tanh(y(5)) + 1.5*tanh(y(6)) ...
- 1.7*tanh(y_d(1)) + 2.7*tanh(y_d(2)) ...
- 2.4*tanh(y_d(5)) + 1.6*tanh(y_d(6)) ...
+ min3 + max3 + 2; % dot{v}_2^R
% v2^I方程中的min/max项
A4 = -1.6*tanh(y_d(1)) + 1.5*tanh(y_d(2));
B4 = -1.6*tanh(y_d(5)) + 1.1*tanh(y_d(6));
min4 = min(A4, B4);
C4 = -1.6*tanh(y_d(1)) + 0.5*tanh(y_d(2));
D4 = 0.6*tanh(y_d(5)) + 2.8*tanh(y_d(6));
max4 = max(C4, D4);
dydt(8) = -0.4*y(8) - 1.6*y(6) + 0.6*tanh(y(1)) + 1.2*tanh(y(2)) ...
- 1.5*tanh(y(5)) + 1.0*tanh(y(6)) ...
- 2.7*tanh(y_d(1)) - 1.7*tanh(y_d(2)) ...
- 1.6*tanh(y_d(5)) - 2.4*tanh(y_d(6)) ...
+ min4 + max4; % dot{v}_2^I
end
function plot_results(sol_master, sol_slave)
% 创建主系统图形窗口
figure('Name', 'Master System', 'Position', [100, 100, 1200, 800])
% 节点1的状态
subplot(2,2,1)
plot(sol_master.x, sol_master.y(1:2,:), 'LineWidth', 1.5)
title('Master Node 1: \kappa States')
legend('\kappa_1^R', '\kappa_1^I')
xlabel('Time t')
ylabel('State Value')
grid on
subplot(2,2,2)
plot(sol_master.x, sol_master.y(3:4,:), 'LineWidth', 1.5)
title('Master Node 1: w States')
legend('w_1^R', 'w_1^I')
xlabel('Time t')
ylabel('State Value')
grid on
% 节点2的状态
subplot(2,2,3)
plot(sol_master.x, sol_master.y(5:6,:), 'LineWidth', 1.5)
title('Master Node 2: \kappa States')
legend('\kappa_2^R', '\kappa_2^I')
xlabel('Time t')
ylabel('State Value')
grid on
subplot(2,2,4)
plot(sol_master.x, sol_master.y(7:8,:), 'LineWidth', 1.5)
title('Master Node 2: w States')
legend('w_2^R', 'w_2^I')
xlabel('Time t')
ylabel('State Value')
grid on
% 创建从系统图形窗口
figure('Name', 'Slave System', 'Position', [100, 100, 1200, 800])
% 节点1的状态
subplot(2,2,1)
plot(sol_slave.x, sol_slave.y(1:2,:), 'LineWidth', 1.5)
title('Slave Node 1: \lambda States')
legend('\lambda_1^R', '\lambda_1^I')
xlabel('Time t')
ylabel('State Value')
grid on
subplot(2,2,2)
plot(sol_slave.x, sol_slave.y(3:4,:), 'LineWidth', 1.5)
title('Slave Node 1: v States')
legend('v_1^R', 'v_1^I')
xlabel('Time t')
ylabel('State Value')
grid on
% 节点2的状态
subplot(2,2,3)
plot(sol_slave.x, sol_slave.y(5:6,:), 'LineWidth', 1.5)
title('Slave Node 2: \lambda States')
legend('\lambda_2^R', '\lambda_2^I')
xlabel('Time t')
ylabel('State Value')
grid on
subplot(2,2,4)
plot(sol_slave.x, sol_slave.y(7:8,:), 'LineWidth', 1.5)
title('Slave Node 2: v States')
legend('v_2^R', 'v_2^I')
xlabel('Time t')
ylabel('State Value')
grid on
% 创建相空间比较图
figure('Name', 'Phase Space Comparison', 'Position', [100, 100, 1400, 600])
% 节点1的实部比较
subplot(1,2,1)
plot(sol_master.x, sol_master.y(1,:), 'b-', 'LineWidth', 1.5)
hold on
plot(sol_slave.x, sol_slave.y(1,:), 'r--', 'LineWidth', 1.5)
title('Node 1 Real Part Comparison')
legend('Master \kappa_1^R', 'Slave \lambda_1^R')
xlabel('Time t')
ylabel('State Value')
grid on
% 节点1的虚部比较
subplot(1,2,2)
plot(sol_master.x, sol_master.y(2,:), 'b-', 'LineWidth', 1.5)
hold on
plot(sol_slave.x, sol_slave.y(2,:), 'r--', 'LineWidth', 1.5)
title('Node 1 Imaginary Part Comparison')
legend('Master \kappa_1^I', 'Slave \lambda_1^I')
xlabel('Time t')
ylabel('State Value')
grid on
end
function analyze_synchronization(sol_master, sol_slave)
% 同步误差分析
figure('Name', 'Synchronization Error', 'Position', [100, 100, 1200, 800])
% 插值使时间点对齐
t_common = unique(sort([sol_master.x, sol_slave.x]));
master_k1R = interp1(sol_master.x, sol_master.y(1,:), t_common);
slave_l1R = interp1(sol_slave.x, sol_slave.y(1,:), t_common);
error_R = abs(master_k1R - slave_l1R);
master_k1I = interp1(sol_master.x, sol_master.y(2,:), t_common);
slave_l1I = interp1(sol_slave.x, sol_slave.y(2,:), t_common);
error_I = abs(master_k1I - slave_l1I);
% 绘制同步误差
semilogy(t_common, error_R, 'b-', 'LineWidth', 1.5)
hold on
semilogy(t_common, error_I, 'r--', 'LineWidth', 1.5)
title('Synchronization Error (Node 1)')
legend('Real Part Error', 'Imaginary Part Error', 'Location', 'best')
xlabel('Time t')
ylabel('Error Magnitude (log scale)')
grid on
% 计算平均同步误差
avg_error_R = mean(error_R(t_common > 5)); % 忽略初始瞬态
avg_error_I = mean(error_I(t_common > 5));
fprintf('\nSynchronization Analysis (Node 1):\n');
fprintf('Average Real Part Error (t>5): %.4e\n', avg_error_R);
fprintf('Average Imaginary Part Error (t>5): %.4e\n', avg_error_I);
if avg_error_R < 1e-4 && avg_error_I < 1e-4
fprintf('System achieved synchronization!\n');
else
fprintf('System did not achieve full synchronization.\n');
end
end
检查一下这个matlab代码是否完整的将下面latex中的公式完美无误写出,有错误的话知名并给出改正后完整代码
For node $l=1$:
\begin{align}
\dot{\kappa}_1^R(t) &= -\kappa_1^R(t) + w_1^R(t) \\
\dot{\kappa}_1^I(t) &= -\kappa_1^I(t) + w_1^I(t) \\
\dot{w}_1^R(t) &= -w_1^R(t) - 0.4\kappa_1^R(t) + 1.5\tanh(\kappa_1^R(t)) - 2.6\tanh(\kappa_1^I(t)) - 2.0\tanh(\kappa_2^R(t)) - 1.7\tanh(\kappa_2^I(t)) \notag \\
&\quad + 2.5\tanh(\kappa_1^R(t-1)) - 1.5\tanh(\kappa_1^I(t-1)) + 1.0\tanh(\kappa_2^R(t-1)) + 1.2\tanh(\kappa_2^I(t-1)) \notag \\
&\quad + \min\left\{
\begin{array}{c}
0.4\tanh(\kappa_1^R(t-1)) + 1.0\tanh(\kappa_1^I(t-1)) \\
-2.0\tanh(\kappa_2^R(t-1)) + 0.3\tanh(\kappa_2^I(t-1))
\end{array}
\right\} \notag \\
&\quad + \max\left\{
\begin{array}{c}
0.2\tanh(\kappa_1^R(t-1)) + 2.5\tanh(\kappa_1^I(t-1)) \\
2.0\tanh(\kappa_2^R(t-1)) + 1.4\tanh(\kappa_2^I(t-1))
\end{array}
\right\} + 2 \\
\dot{w}_1^I(t) &= -w_1^I(t) - 0.4\kappa_1^I(t) + 2.6\tanh(\kappa_1^R(t)) + 1.5\tanh(\kappa_1^I(t)) + 1.7\tanh(\kappa_2^R(t)) - 2.0\tanh(\kappa_2^I(t)) \notag \\
&\quad + 1.5\tanh(\kappa_1^R(t-1)) + 2.5\tanh(\kappa_1^I(t-1)) - 1.2\tanh(\kappa_2^R(t-1)) + 1.0\tanh(\kappa_2^I(t-1)) \notag \\
&\quad + \min\left\{
\begin{array}{c}
-1.0\tanh(\kappa_1^R(t-1)) + 0.4\tanh(\kappa_1^I(t-1)) \\
-0.3\tanh(\kappa_2^R(t-1)) - 2.0\tanh(\kappa_2^I(t-1))
\end{array}
\right\} \notag \\
&\quad + \max\left\{
\begin{array}{c}
-2.5\tanh(\kappa_1^R(t-1)) + 0.2\tanh(\kappa_1^I(t-1)) \\
-1.4\tanh(\kappa_2^R(t-1)) + 2.0\tanh(\kappa_2^I(t-1))
\end{array}
\right\}
\end{align}
For node $l=2$:
\begin{align}
\dot{\kappa}_2^R(t) &= -\kappa_2^R(t) + w_2^R(t) \\
\dot{\kappa}_2^I(t) &= -\kappa_2^I(t) + w_2^I(t) \\
\dot{w}_2^R(t) &= -0.4w_2^R(t) - 1.6\kappa_2^R(t) + 1.2\tanh(\kappa_1^R(t)) - 0.6\tanh(\kappa_1^I(t)) + 1.0\tanh(\kappa_2^R(t)) + 1.5\tanh(\kappa_2^I(t)) \notag \\
&\quad - 1.7\tanh(\kappa_1^R(t-1)) + 2.7\tanh(\kappa_1^I(t-1)) - 2.4\tanh(\kappa_2^R(t-1)) + 1.6\tanh(\kappa_2^I(t-1)) \notag \\
&\quad + \min\left\{
\begin{array}{c}
1.5\tanh(\kappa_1^R(t-1)) + 1.6\tanh(\kappa_1^I(t-1)) \\
1.1\tanh(\kappa_2^R(t-1)) + 1.6\tanh(\kappa_2^I(t-1))
\end{array}
\right\} \notag \\
&\quad + \max\left\{
\begin{array}{c}
0.5\tanh(\kappa_1^R(t-1)) + 1.6\tanh(\kappa_1^I(t-1)) \\
2.8\tanh(\kappa_2^R(t-1)) - 0.6\tanh(\kappa_2^I(t-1))
\end{array}
\right\} + 2 \\
\dot{w}_2^I(t) &= -0.4w_2^I(t) - 1.6\kappa_2^I(t) + 0.6\tanh(\kappa_1^R(t)) + 1.2\tanh(\kappa_1^I(t)) - 1.5\tanh(\kappa_2^R(t)) + 1.0\tanh(\kappa_2^I(t)) \notag \\
&\quad - 2.7\tanh(\kappa_1^R(t-1)) - 1.7\tanh(\kappa_1^I(t-1)) - 1.6\tanh(\kappa_2^R(t-1)) - 2.4\tanh(\kappa_2^I(t-1)) \notag \\
&\quad + \min\left\{
\begin{array}{c}
-1.6\tanh(\kappa_1^R(t-1)) + 1.5\tanh(\kappa_1^I(t-1)) \\
-1.6\tanh(\kappa_2^R(t-1)) + 1.1\tanh(\kappa_2^I(t-1))
\end{array}
\right\} \notag \\
&\quad + \max\left\{
\begin{array}{c}
-1.6\tanh(\kappa_1^R(t-1)) + 0.5\tanh(\kappa_1^I(t-1)) \\
0.6\tanh(\kappa_2^R(t-1)) + 2.8\tanh(\kappa_2^I(t-1))
\end{array}
\right\}
\end{align}
\section*{Real-valued Slave System}
For node $l=1$:
\begin{align}
\dot{\lambda}_1^R(t) &= -\lambda_1^R(t) + v_1^R(t) \\
\dot{\lambda}_1^I(t) &= -\lambda_1^I(t) + v_1^I(t) \\
\dot{v}_1^R(t) &= -v_1^R(t) - 0.4\lambda_1^R(t) + 1.5\tanh(\lambda_1^R(t)) - 2.6\tanh(\lambda_1^I(t)) - 2.0\tanh(\lambda_2^R(t)) - 1.7\tanh(\lambda_2^I(t)) \notag \\
&\quad + 2.5\tanh(\lambda_1^R(t-1)) - 1.5\tanh(\lambda_1^I(t-1)) + 1.0\tanh(\lambda_2^R(t-1)) + 1.2\tanh(\lambda_2^I(t-1)) \notag \\
&\quad + \min\left\{
\begin{array}{c}
0.4\tanh(\lambda_1^R(t-1)) + 1.0\tanh(\lambda_1^I(t-1)) \\
-2.0\tanh(\lambda_2^R(t-1)) + 0.3\tanh(\lambda_2^I(t-1))
\end{array}
\right\} \notag \\
&\quad + \max\left\{
\begin{array}{c}
0.2\tanh(\lambda_1^R(t-1)) + 2.5\tanh(\lambda_1^I(t-1)) \\
2.0\tanh(\lambda_2^R(t-1)) + 1.4\tanh(\lambda_2^I(t-1))
\end{array}
\right\} + 2 \\
\dot{v}_1^I(t) &= -v_1^I(t) - 0.4\lambda_1^I(t) + 2.6\tanh(\lambda_1^R(t)) + 1.5\tanh(\lambda_1^I(t)) + 1.7\tanh(\lambda_2^R(t)) - 2.0\tanh(\lambda_2^I(t)) \notag \\
&\quad + 1.5\tanh(\lambda_1^R(t-1)) + 2.5\tanh(\lambda_1^I(t-1)) - 1.2\tanh(\lambda_2^R(t-1)) + 1.0\tanh(\lambda_2^I(t-1)) \notag \\
&\quad + \min\left\{
\begin{array}{c}
-1.0\tanh(\lambda_1^R(t-1)) + 0.4\tanh(\lambda_1^I(t-1)) \\
-0.3\tanh(\lambda_2^R(t-1)) - 2.0\tanh(\lambda_2^I(t-1))
\end{array}
\right\} \notag \\
&\quad + \max\left\{
\begin{array}{c}
-2.5\tanh(\lambda_1^R(t-1)) + 0.2\tanh(\lambda_1^I(t-1)) \\
-1.4\tanh(\lambda_2^R(t-1)) + 2.0\tanh(\lambda_2^I(t-1))
\end{array}
\right\}
\end{align}
For node $l=2$:
\begin{align}
\dot{\lambda}_2^R(t) &= -\lambda_2^R(t) + v_2^R(t) \\
\dot{\lambda}_2^I(t) &= -\lambda_2^I(t) + v_2^I(t) \\
\dot{v}_2^R(t) &= -0.4v_2^R(t) - 1.6\lambda_2^R(t) + 1.2\tanh(\lambda_1^R(t)) - 0.6\tanh(\lambda_1^I(t)) + 1.0\tanh(\lambda_2^R(t)) + 1.5\tanh(\lambda_2^I(t)) \notag \\
&\quad - 1.7\tanh(\lambda_1^R(t-1)) + 2.7\tanh(\lambda_1^I(t-1)) - 2.4\tanh(\lambda_2^R(t-1)) + 1.6\tanh(\lambda_2^I(t-1)) \notag \\
&\quad + \min\left\{
\begin{array}{c}
1.5\tanh(\lambda_1^R(t-1)) + 1.6\tanh(\lambda_1^I(t-1)) \\
1.1\tanh(\lambda_2^R(t-1)) + 1.6\tanh(\lambda_2^I(t-1))
\end{array}
\right\} \notag \\
&\quad + \max\left\{
\begin{array}{c}
0.5\tanh(\lambda_1^R(t-1)) + 1.6\tanh(\lambda_1^I(t-1)) \\
2.8\tanh(\lambda_2^R(t-1)) - 0.6\tanh(\lambda_2^I(t-1))
\end{array}
\right\} + 2 \\
\dot{v}_2^I(t) &= -0.4v_2^I(t) - 1.6\lambda_2^I(t) + 0.6\tanh(\lambda_1^R(t)) + 1.2\tanh(\lambda_1^I(t)) - 1.5\tanh(\lambda_2^R(t)) + 1.0\tanh(\lambda_2^I(t)) \notag \\
&\quad - 2.7\tanh(\lambda_1^R(t-1)) - 1.7\tanh(\lambda_1^I(t-1)) - 1.6\tanh(\lambda_2^R(t-1)) - 2.4\tanh(\lambda_2^I(t-1)) \notag \\
&\quad + \min\left\{
\begin{array}{c}
-1.6\tanh(\lambda_1^R(t-1)) + 1.5\tanh(\lambda_1^I(t-1)) \\
-1.6\tanh(\lambda_2^R(t-1)) + 1.1\tanh(\lambda_2^I(t-1))
\end{array}
\right\} \notag \\
&\quad + \max\left\{
\begin{array}{c}
-1.6\tanh(\lambda_1^R(t-1)) + 0.5\tanh(\lambda_1^I(t-1)) \\
0.6\tanh(\lambda_2^R(t-1)) + 2.8\tanh(\lambda_2^I(t-1))
\end{array}
\right\}
\end{align}
\( \kappa_1(\phi) = 1.3 + 1.1i \), \( w_1(\phi) = 3.0 - 1.8i \), \( \kappa_2(\phi) = -2.0 - 1.2i \), \( w_2(\phi) = -1.0 + 1.3i \). \(\lambda_1(\phi) = 1.8 + 1.7i\), \(\dot{\lambda}_1(\phi) = 2.1 - 1.4i\), \(\lambda_2(\phi) = -2.5 - 1.4i\), \(\dot{\lambda}_2(\phi) = -1.8 + 1.0i\), \(\phi \in [-1, 0]\).
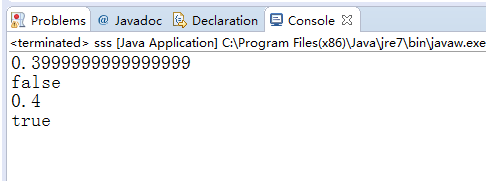





 本文深入探讨了Java中浮点数运算的不精确性及其解决方法,通过代码演示展示了使用BigDecimal类进行精确计算的过程与结果,旨在帮助开发者避免常见的精度错误。
本文深入探讨了Java中浮点数运算的不精确性及其解决方法,通过代码演示展示了使用BigDecimal类进行精确计算的过程与结果,旨在帮助开发者避免常见的精度错误。
















 1562
1562

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








