乘法公式
二倍角公式
维基百科,自由的百科全书
二倍角公式 是数学 三角函数 中常用的一组公式,通过角α 的三角函数值的一些变换关系来表示其二倍角2α 的三角函数值,二倍角公式包括正弦二倍角公式、余弦二倍角公式以及正切二倍角公式。二倍角公式均可通过和角公式 推出。
正弦二倍角公式
此式就是正弦二倍角公式 :
[编辑 ] 余弦二倍角公式
余弦二倍角公式 有三组表示形式,三组形式等价:
[编辑 ] 正切二倍角公式
此式就是正切二倍角公式 :
-

-
-
诱导公式
诱导公式 是数学 三角函数 中将角度比较大的三角函数利用角 的周期性,转换为角度比较小的三角函数。主要有以下几条变换公式:
-
公式一
- sin(2kπ+α)=sinα
- cos(2kπ+α)=cosα
- tan(2kπ+α)=tanα
- cot(2kπ+α)=cotα
[编辑 ] 公式二
- sin(2π-α)=-sinα
- cos(2π-α)=cosα
- tan(2π-α)=-tanα
- cot(2π-α)=-cotα
[编辑 ] 公式三
- sin(π+α)=-sinα
- cos(π+α)=-cosα
- tan(π+α)=tanα
- cot(π+α)=cotα
[编辑 ] 公式四
- sin(π-α)=sinα
- cos(π-α)=-cosα
- tan(π-α)=-tanα
- cot(π-α)=-cotα
[编辑 ] 公式五
- sin(-α)=-sinα
- cos(-α)=cosα
- tan(-α)=-tanα
- cot(-α)=-cotα
[编辑 ] 公式六
- sin(π/2+α)=-cosα
- cos(π/2+α)=sinα
- tan(π/2+α)=-cotα
- cot(π/2+α)=-tanα
- sin(π/2-α)=cosα
- cos(π/2-α)=sinα
- tan(π/2-α)=cotα
- cot(π/2-α)=tanα
值得注意的是,公式一至六其实是存在着内在联系的,可以写成以下形式:
- sin(kπ/2+α)
- cos(kπ/2+α)
- tan(kπ/2+α)
- cot(kπ/2+α)
(k∈Z)
可用如下口诀将联系记忆起来:“奇变偶不变,符号看象限 ”。意思为,当K为奇数 时,sin变为cos,cos变为sin,tan变为cot,cot变为tan,而K为偶数 时,三角函数则不变换。
对于正负号,则要看最后角所在的象限进行判断。
角平分线长公式
维基百科,自由的百科全书
在数学 中,角平分线长公式 是已知三角形 三条边的长度 时计算内角平分线 长度的公式。在三角形
 ABC中, 若将角A的角平分线记为t a , 角B的角平分线记为t b , 角C的角平分线记为t c , 那么它们长度可用如下公式计算:
ABC中, 若将角A的角平分线记为t a , 角B的角平分线记为t b , 角C的角平分线记为t c , 那么它们长度可用如下公式计算:-
t a =
 ,
,
-
t b =
 ,
,
-
t c =
 ,
,
其中的s 是半周长。
[编辑 ] 推导
如右图,设BE为
 ABC中角B的平分线,交边AC于E,则
ABC中角B的平分线,交边AC于E,则 ABE=
ABE= EBC,BE=t b 。下面证明角平分线长
EBC,BE=t b 。下面证明角平分线长-
t b =
 。
。
首先, °(互为邻补角 ),因此有
°(互为邻补角 ),因此有  =
= 。
。根据正弦定理 ,在三角形ABE中,
 ,即
,即 。同样地,在三角形BCE中,
。同样地,在三角形BCE中, ,也就是
,也就是 。 另一方面,
。 另一方面, ,并且
,并且 ,因此得到
,因此得到 。 注意到x + y = b ,代入上式,消去x 之后就可得到
。 注意到x + y = b ,代入上式,消去x 之后就可得到 。
。接下来,在三角形BCE中,根据余弦定理 ,有:
-
 ....(1)
....(1)
-
然而
 ,把
,把
 以及
y 的表达式代入(1)式中,得到
以及
y 的表达式代入(1)式中,得到
-

化简之后就可以得到角平分线长公式:
-

-
设s为半周长, 即
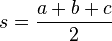 ,则可以将公式写成
,则可以将公式写成
-

-

同理,可证得其他两式。
海伦公式
假设有一个三角形,边长分别为a ,b ,c ,三角形的面积S 可由以下公式求得:






 。
。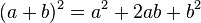 。
。

 。
。 。
。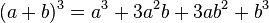 。
。 。
。 。
。 。
。 。
。 。
。




 ,这里
,这里
 。
。




























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








