An inequality about sine function

最新推荐文章于 2024-01-23 22:51:07 发布

最新推荐文章于 2024-01-23 22:51:07 发布 · 59 阅读

文章标签：

#BBS #PHP #Blog #F#

本文通过Fourier级数分析法证明了一个与正弦函数相关的不等式，并指出该不等式在所有极小值点处成立。此外，还发现该不等式对应的函数在这些极小值点上的取值构成了离散正弦变换。

A problem provided by me and solved by mathe in bbs.emath.ac.cn(See: http://zdu.spaces.live.com/blog/cns!C95152CB25EF2037!136.entry)

In http://bbs.emath.ac.cn/viewthread.php?tid=49&page=1&fromuid=20#pid159, northwolves asked for an inequality related to sine function:
For all ,it is easy to prove that:

The problem is whether: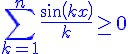
$\sum_{k=1}^n {sin(kx)}/k>=0$ for all .

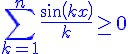According to 7#, we could find the all minima of the function . They're for all integer k. So we only need prove the $\sum_{k=1}^n {sin(kx)}/k>=0$ for all those minima.

In 14#, Fourier Series are used to analyze the problem, first we have:
let g(t,x)=sin(x)+sin(2x)+...+sin(tx)

So let , we get

where the left side is Fourier series of .
So we have .
We need only prove the right side is no more than 0 for all those minima. Let , we need prove or . This function will first increase and then decrease. So we only need to prove it is true for both the smallest and largest minima. It means we need prove that
for , the inequality is true.
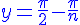It is easy to verify that the inequality is true for both and 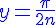when n is at least 3. So we could prove the problem for n is at least 3. And the problem for n is 1 and 2 has been proved in advance. So the original inequality is proved.

Another interested attribute of this inequality as pointed out in 9# is that the value of function F(x) at all those minima forms the Discrete Sine Transformation of . So this inequality also proves that each item of Discrete Sine Transformation of is non-negative.