数据科学 9 决策树（概念）

主要内容：
•决策树建模思路
•Quinlan系列决策树(ID3、 C4.5、 C8.0)建模原理
•CART建模原理
•模型修剪
•模型评估
•随机森林与组合算法

9.1 决策树算法核心

• 该按什么样的次序来选择变量（属性）？
• 最佳分离点（连续的情形）在哪儿？

9.1.1 拆分规则

9.2 Quinlan系列决策树建模原理

9.2.1 ID3决策树

ID3、 C4.5、 C5.0

1、ID3决策树原理

步骤:

• 建树：
  • 选择最有解释力度的变量
  • 对于每个变量选择最优分割点
• 剪树：
  • 前向剪枝：控制生成树的规模
  • 后项剪枝：删除没有意义的分组

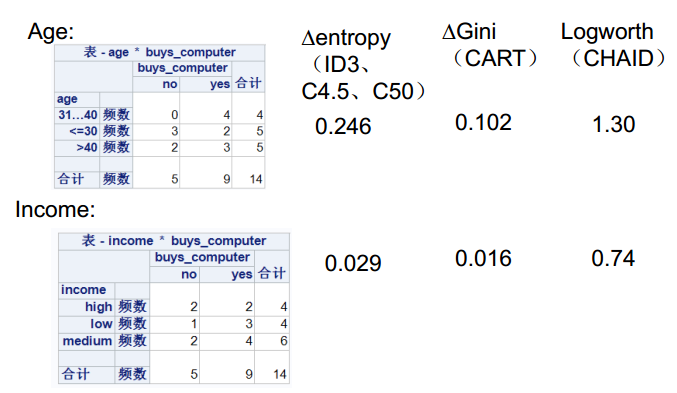
2、理论-信息增益计算

ID3输入为分类变量，选取信息增益高的变量作为分裂属性。

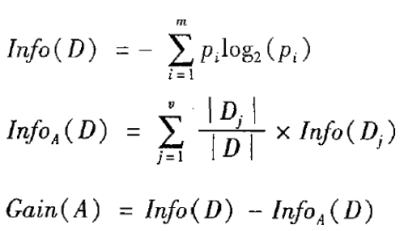
3、缺点

• 倾向于选择水平数量较多的变量
• 输入变量必须是分类变量 (连续变量必须离散化)

9.2.2 C4.5 决策树

1、原理

• 增加了连续变量二分法；
• 信息增益的方法倾向于首先选择因子数较多的变量
• 信息增益的改进： 增益率
  
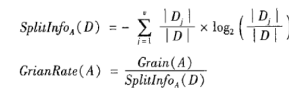
  说明：
  说明: C4.5决策树不能处理等级变量，要么作为分类变量，要么作为连续变量。这需要分析人员提前设置好。设为因子类型即为分类变量，否则为连续变量。

2、单个分类或等级变量

1）、决策树遍历搜索

• 对于分类变量，假设该输入变量有4个水平，则依次遍历所有的组合形式，计算熵增益率最大的那个组合方式

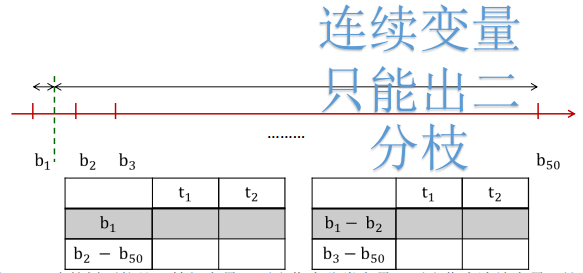
2）、决策树分割搜索

• 对于连续变量，先等宽方式分为50组，依次取阀值分割成两组，计算熵增益率最大的那个分割方式

3、比较多各变量的优先级

1）、假设都是连续变量，先各自做分割，并计算每个分割的熵增益率。
2）、比较每个变量所能达到的最大熵增益率，取最大的那个作为本次分割选择的变量，该变量对应最大熵增益率的分割点作为分割依据。

9.2.3 R中的C5.0 算法(Python目前没有实现)

9.2.4 CART决策树

1、CART决策树原理

步骤:

• 建树：
  • 选择最有解释力度的变量
  • 对于每个变量选择最优分割点
• 剪树：
  • 前向剪枝：控制生成树的规模
  • 后项剪枝：删除没有意义的分组

2、基尼系数的计算

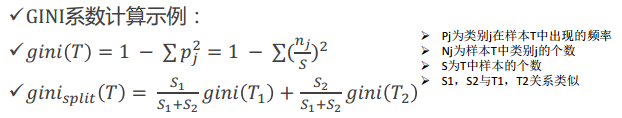
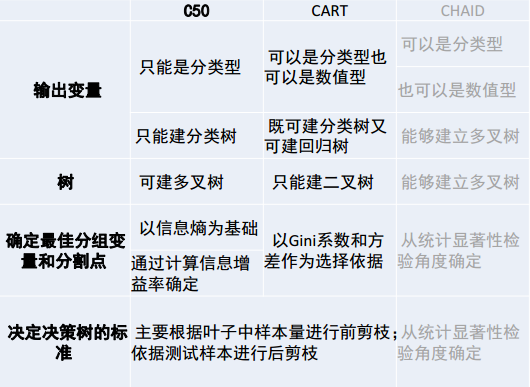
9.2.5 决策树方法总结

9.2.5 模型修剪——以CART为例

1、预修剪

其目标是控制决策树充分生长，可以事先指定一些控制参数，包括：
（1）决策树最大深度。如果决策树的层数已经达到指定深度，则停止生长 。
（2）树中父节点和子节点的最少样本量或比例。对于父节点，如果节点的样本量低于最小样本量或比例，则不再分组；对于子节点，如果分组后生成的子节点的样本量低于最小样本量或比例，则不必进行分组 。
（3）树节点中输出变量的最小异质性减少量。如果分组产生的输出变量异质性变化量小于一个指定值，则不必进行分组。

2、后剪枝

后修剪技术允许决策树充分生长，然后在此基础上根据一定的规则，剪去决策树中那些不具有一般代表性的叶节点或子树，是一个边修剪边检验的过程。在修剪过程中，应不断计算当前决策子树对测试样本集的预测精度或误差，并判断应继续修剪还是停止修剪。
•CART采用的后修剪技术称为最小代价复杂性修剪法（Minimal Cost Complexity Pruning,MCCP）
•MCCP有这样的基本考虑：首先，考虑的决策树虽然对训练样本有很好的预测精度，但在测试样本和未来新样本上不会仍有令人满意的预测效果；其次，理解和应用一棵复杂的决策是一个复杂过程。因此，决策树修剪的目标是得到一棵“恰当”的树，它首先要具有一定的预测精度，同时决策树的复杂程度应是恰当的。

CART选择最终子树标准是：选择交叉验证中错误最小的

3、CART的决策树修剪方法—总结

• 输入变量（自变量）：为分类型变量或连续型变量
• 输出变量（目标变量）：为分类型变量（或连续型：回归分析）
• 连续变量处理： N等分离散化
• 树分枝类型：二分枝
• 分割指标： gini增益（分割后的目标变量取值变异较小，纯度高）
• 先剪枝：决策树最大深度、最小样本分割数、叶节点包含的最小样本数、复杂度系数最小值
• 后剪枝：使用最小代价复杂度剪枝法