K-Means算法原理及numpy实现

K-Means应该是大多数人接触到的第一个聚类算法或无监督学习算法，其算法原理简单，Python实现（使用sklearn包）也很方便。同时K-Means算法对于高维聚类（在维度没有达到几十维的情况下）也非常快速有效。我之前也是使用sklearn自带的kMeans包进行数据聚类的，但随着实验的深入，也发现了使用算法库带来的诸多不便，如不能自定义距离计算公式等。而网上的一些完全基于numpy编写的K-Means代码，由于受其自身开源性和可扩展性的影响，导致代码冗长繁杂，对初学者并不十分友好，于是动手实现了一下K-Means，力求简单易懂，同时保持一定的可扩展性，在此与大家分享。

---

算法原理

首先简单介绍一些K-Means的原理：字面上，K即原始数据最终被聚为K类或分为K类，Means即均值点。K-Means的核心就是将一堆数据聚集为K个簇，每个簇中都有一个中心点称为均值点，簇中所有点到该簇的均值点的距离都较到其他簇的均值点更近。如下图是一个K=4的聚类示意图，每个点都是到自己所在的簇的均值点更近，而这个均值点可以是原始数据中的点，也可以是一个不存在的点，即不属于原始数据集中的点。

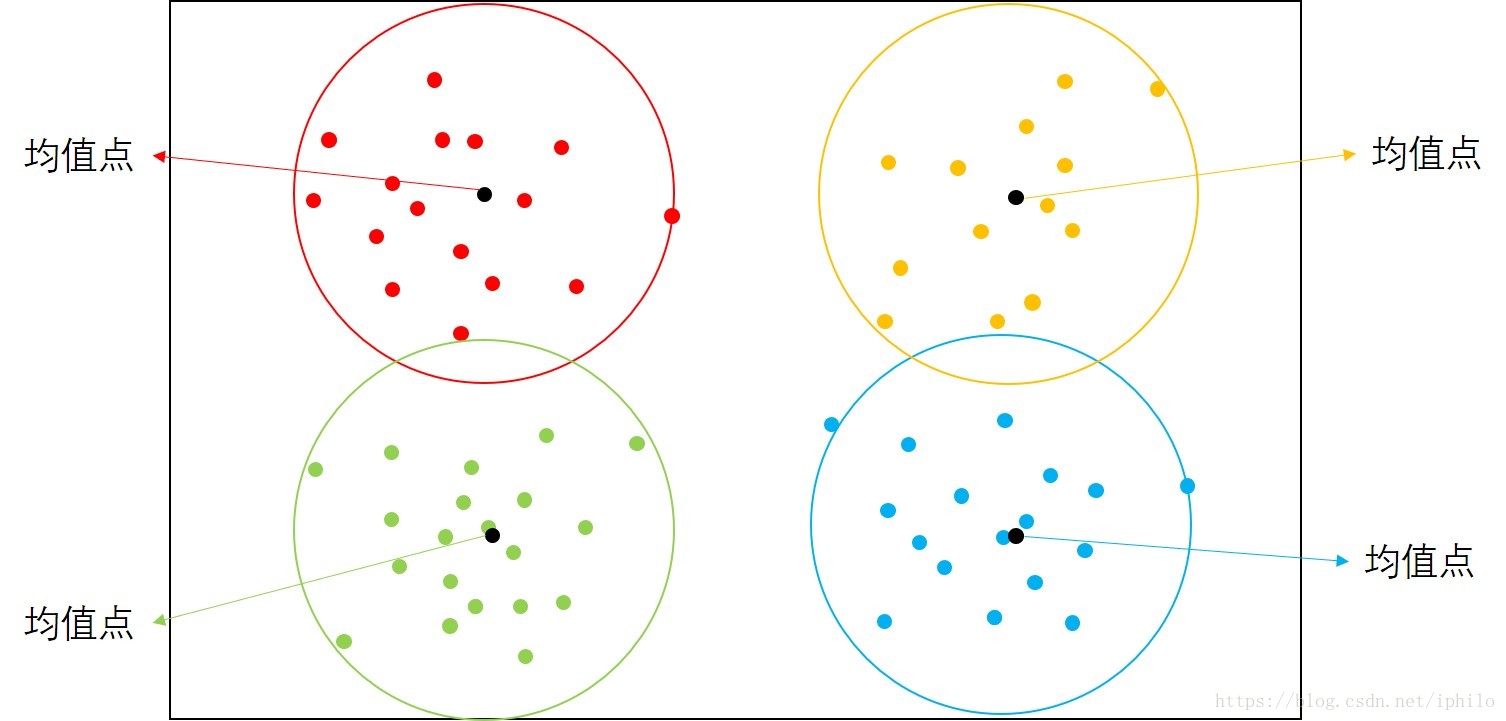
K-Means的算法流程下图所示，这里使用的是周志华教授《机器学习》一书中的插图。用文字描述为：

1. 首先确定K值（即你想把数据聚为几类，K值是K-Means算法中唯一的参数）；
2. 从原始数据集中随机选择K个点作为初始均值点（步骤1和2为准备工作）；
3. 依次从原始数据集中取出数据，每取出一个数据就和K个均值点分别计算距离（默认计算点间的欧氏距离），和谁更近就归为这个均值点所在的簇；
4. 当步骤3结束后，分别计算各簇当前的均值点（即求该簇中所有点的平均值）；
5. 比较当前的均值点和上一步得到的均值点是否相同，如果相同，则K-Means算法结束，否则，将当前的均值点替换掉之前的均值点，然后重复步骤3。
   

---

使用sklearn包尝试聚类

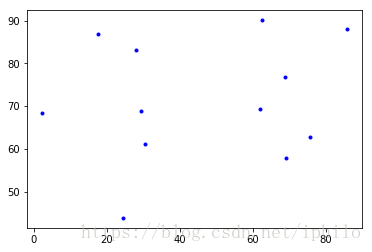
接下来我们使用sklearn包中的KMeans算法库尝试聚类过程。这里给出12个点，将它们的横纵坐标分别存储。

from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

x = [2.273, 27.89, 30.519, 62.049, 29.263, 62.657, 75.735, 24.344, 17.667, 68.816, 69.076, 85.691]
y = [68.367, 83.127, 61.07, 69.343, 68.748, 90.094, 62.761, 43.816, 86.765, 76.874, 57.829, 88.114]
plt.plot(x, y, 'b.')
plt.show()

points = [[i,j] for i,j in zip(x,y)]#Python递推式，将x和y中的数据依次选出构成点集
y_pred = KMeans(n_clusters=2).fit_predict(points)#将数据聚为2类
print('聚类结果：', y_pred)#打印聚类的结果
plt.scatter(x, y, c=y_pred, marker='*')
plt.show()

运行结果为：

聚类结果：[0 0 0 1 0 1 1 0 0 1 1 1]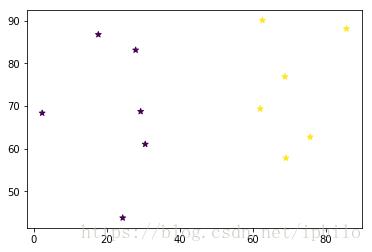

可以看到使用算法包使得程序十分简洁，其中y_pred表示每个点在聚类后被归为哪一类，由于其数据恰为int型，所以可以用其为原始数据点进行着色，以体现聚类结果。但是使用算法包存在两个问题：首先该算法包默认使用的是欧氏距离来计算点与点的距离的，如果我们想替换为曼哈顿距离、夹角余弦等其它距离计算公式时，就难以实现了；其次聚类的过程对我们是不可见的，我们能看到的只是聚类后的结果。这里第一个问题属于“刚需”，很多人都会遇到，第二个问题可能初学者才会遇到（实际上动手撸代码也是受学弟之托，他们老师要求把每一步聚类的结果都写出来，可能部分同学也遇到过这个问题吧……）。

---

完全基于numpy编写K-Means代码

首先上代码，然后再对代码做解释。

import numpy as np
import matplotlib.pyplot as plt

'''标志位统计递归运行次数'''
flag = 0

'''欧式距离'''
def