Visit: https://zhuanlan.zhihu.com/p/478083833
Chapter one: Introduce
Reinforcement learning
-
强化学习构建每个环境状态到动作的映射,以最大化reward signal(回报信号)为目标
-
强化学习最显著的特征是:trial-and-error search(试错搜索)和delayed reward(延迟收益)。
-
马尔可夫决策过程包含三个主要方面:sense(感知),action(动作)和goal(目标)。
-
强化学习有别于监督学习和无监督学习
1.监督学习基于标签,每个样本描述特征空间中一种具体情况,并标注对应的正确动作(决策)。但监督学习在交互行为中表现不好,对于没有学习过的标签不能做出正确反映。而在强化学中,面对未知的状态,智能体要能够从未曾尝试过的一次次试错中学习经验,优化决策。
2.无监督学习重在找出未给出标签的数据背后隐含的结构与规律。而强化学习重在最大化回报信号而不是找出隐含的结构。
-
强化学习独有的挑战是权衡“搜索试探”和“利用开发”——trade-off between exploration and exploition。
-
强化学习会考虑目标引导性的智能体与环境之间的交互。强化学习的智能体有明确的目标,能够感知环境的方方面面以及选择行动去影响环境。
-
一些参数逼近的强化学习方法巧妙地解决了curse of dimensionality(数维灾难)问题。
-
基于一般的原则的搜索和学习被视为“弱方法”,而基于具体的经验知识的方法被视为“强方法”——weak methods and strong methods。
-
现代强化学习的重要成果之一在于与其他学科的有效结合。
1.2 Examples
人和动物是通过直觉来判断环境变化带来的反映,强化学习中用reward signal来代替直觉。
1.3 Elements of Reinforcement Learning
强化学习的动作对象——agent智能体
强化学习的唯一目标——最大化长期总收益
强化学习的四个核心要素:
-
policy:策略,核心,给定环境状态到智能体动作行为的映射
-
reward signal:奖励信号,定义了强化学习问题的目标,反映智能体行为的好坏,是策略和值函数的依据。
-
value function:值函数,一个状态的价值指智能体从该状态开始,对将来累计的总收益的期望。几乎所有强化学习算法中最重要的部分就是高效的值估计算法。
rs与vf比较:回报信号属于即时感知,值函数表征了长期内哪种策略更好
-
model of the environment(optional):环境模型(可选),模仿或推测环境行为变化,一直更新
1.4 limitations and scope
遗传算法,遗传编程,模拟退火等方法不用值函数,而是进行迭代,有一定的机率跳出局部最优解,它们忽略了一些强化学习的东西,这种进化问题本质上不适合用强化学习。
1.5 An extended example:Tic-tac-toe
- 井字棋游戏:遍历棋盘的所有情况,赋初值;用贪婪或
ε-greedy确定策略;更新策略(反推);多次更新后,得到相对较好的胜利方法。 - 强化学习可以与神经网络/深度学习结合,用来更快地得到更好的参数。
1.6 summary
- 强化学习方法是一种以目标为导向,集感知、自主试错学习及制定决策于一体的计算方法。
- 策略空间中高效搜索得益于关键的值函数方法。
1.7 Early History of Reinforcement Learning
强化学习的早期历史
Chapter two: Multi-armed Banits
区分强化学习与监督(模仿)学习等其他类型学习的最重要特征:强化学习使用训练信息来评估所采取的行动,而不是通过给予正确的行动来指导。
A k-armed Bandit Problem
多臂赌博机问题:k个摇臂,摇动每个摇臂得到的回报都遵循一种概率分布,如何摇动N次最大化预期总奖励。
多臂赌博机是一个非序贯决策问题,无状态的转移,选择动作aaa的预期奖励:q∗(a)=E[Rt∣At=a]{q_*(a)=E[R_t|A_t=a]}q∗(a)=E[Rt∣At=a],在时间步骤t{t}t的动作a{a}a的估计值Qt(a){Q_t(a)}Qt(a),我们希望Qt(a)=q∗(a){Q_t(a)=q_*(a)}Qt(a)=q∗(a)。
实际上如果知道每一个动作的value,那么很容易使用贪婪策略选最大的value对应的动作,而实际上不知道。因此进行多次实验,以回报值最高的作为选择的策略。
动作的选择需要平衡探索与利用,利用是进一步最大化预期奖励的正确做法,但探索可能会产生更大的长期总回报。
Action-value Methods
以平均实际收到的奖励估算行动价值:
Qt(a)=∑i=1t−1Ri⋅I(Ai=a)∑i=1t−1I(Ai=a)
Q_t(a)=\frac{\sum_{i=1}^{t-1}R_i·I(A_i=a)}{\sum_{i=1}^{t-1}I(A_i=a)}
Qt(a)=∑i=1t−1I(Ai=a)∑i=1t−1Ri⋅I(Ai=a)
其中I为指示函数,逻辑值为真取1,否则取0
根据估算进行行动选择决策:
a={arg maxa q(a)greedy{arg maxa q(a)with p=1-ϵrandom choicewith p=ϵϵ−greedy
a=\left\{
\begin{matrix}
{\underset {a}{\operatorname {arg\,max} }}\,q(a)\quad\quad\quad\quad\quad\quad\quad greedy \\
\left\{
\begin{matrix}
{\underset {a}{\operatorname {arg\,max} }}\,q(a)\quad
\text{with p=1-}\epsilon \\
\text{random choice}\quad\text{with p=}\epsilon
\end{matrix}
\right.
\quad\epsilon-greedy
\end{matrix}
\right.
a=⎩⎨⎧aargmaxq(a)greedy{aargmaxq(a)with p=1-ϵrandom choicewith p=ϵϵ−greedy
The 10-armed Testbed
贪婪策略(可看作特殊的 ε = 0 的 ε-greedy)与ε−greedy{ε-greedy}ε−greedy策略进行对比。以平均回报和正向动作为输出。实验结果表明,在学习次数很少的情况下,贪婪策略更优;次数较多时,在一定范围内,ε{ε}ε越大,效果越好。
Incremental Implementation
在计算层面优化行动值估计为观察到的奖励的样本平均值的问题:增量实现
我们专注于单一动作。式中Ri{R_i}Ri表示在第i{i}i次选择动作之后收到的奖励,Qn{Q_n}Qn为n次选择之后动作价值的估计。
Qn=∑i=1n−1Rin−1
Q_n=\frac{\sum_{i=1}^{n-1}R_i}{n-1}
Qn=n−1∑i=1n−1Ri
通过处理每个新奖励所需的小的,恒定的计算,很容易设计用于更新平均值的增量公式。 给定QnQ_nQn和第nnn个奖励RnR_nRn,所有nnn个奖励的新平均值可以通过下式计算得出:
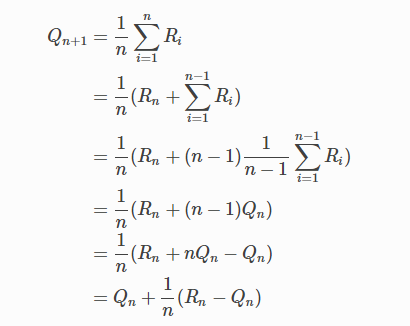
一般形式如下:
新估计←旧估计+步长[目标−旧估计]
k{k}k臂赌博机算法如下:

Tracking a Nonstationary Problem
平均方法适用于固定赌博机问题,即对于其中奖励概率不随时间变化的赌博机问题。而在非稳态强化学习问题中给予最近的奖励比给长期的奖励更重要,因此会使用常量步长参数,即用α{\alpha}α代替增量式中的1n{\frac{1}{n}}n1。
Qn+1=Qn+α(Rn−Qn)
\begin{aligned}
Q_{n+1}=Q_n+\alpha(R_n-Q_n)
\end{aligned}
Qn+1=Qn+α(Rn−Qn)
步长参数 α∈(0,1]{α∈(0,1]}α∈(0,1]是常数,这使得Qn+1{Q_{n+1}}Qn+1是过去奖励和初始估计Q1{Q_{1}}Q1的加权平均值。
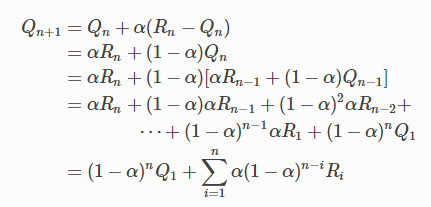
Optimistic Initial Values
均值采样会出现偏差。初始值设为 0 虽然会存在偏差,但很简单,用的最多。但由于会动态衰减,只会影响速率,迭代次数足够多的时候,对结果影响不大。
Upper-Confidence-Bound Action Selection
行动价值估计的准确性始终存在不确定性,因此需要探索。
-
贪婪的行为是目前看起来最好的行动,但其他行动实际上可能更好。
-
ε 贪婪行动选择迫使不贪婪的行动被尝试,而不是那些几乎贪婪或特别不确定的动作。
-
上限置信区间(UCB)根据实际上最优的潜力来选择非贪婪行动,同时考虑到它们的估计与最大值的接近程度以及这些估计中的不确定性。
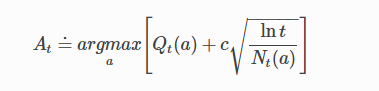
[UCB的想法]
平方根项是对一个值估计的不确定性或方差的度量。因此,最大化的数量是动作a的可能真实值的一种上限,其中c确定置信水平。每次选择a时,不确定性可能会降低:Nt(a){N_t(a)}Nt(a)递增,并且,正如它在分母中出现的那样,不确定性项减少。另一方面,每次选择除a之外的动作时,t增加但Nt(a){N_t(a)}Nt(a)不增加;因为t出现在分子中,不确定性估计值会增加。使用自然对数意味着随着时间的推移,增加量会变小,但是是无限制;最终将选择所有操作,但是将随着时间的推移,具有较低值估计值或已经频繁选择的操作的选择频率会降低。
Gradient Bandit Algorithms

Associative Search (Contextual Bandits)
语境赌博机(略)。
在更一般的强化学习任务中,需要将不同行为与不同情况联系起来,目标是学习策略:从状态到在这些情况下最佳的行为的映射。
Summary
从k{k}k臂赌博机引出几种平衡探索和利用的简单方法:
- ε 贪婪方法随机选择一小部分时间
- UCB方法确定性地选择,但通过巧妙地在每个步骤中有利于目前为止接收到更少样本的动作来实现探索。
- 梯度赌博机算法估计的不是动作价值,而是动作偏好,并且使用soft-max分布以分级的概率方式支持更优选的动作。
- 初始化估计的简单技巧积极地促使甚至贪婪的方法也进行显著探索。
Chapter three: Finite Markov Decision Processes
The Agent–Environment Interface
有限MDP旨在从交互中学习以实现目标,学习决策者被称为智能体,智能体之外与之持续交互的一切被称为环境,智能体选择动作,同时环境响应动作发生状态改变并产生奖励,智能体通过最大化总回报选择最佳策略。
总回报:累积立即回报
策略:给定状态下动作集上的概率分布
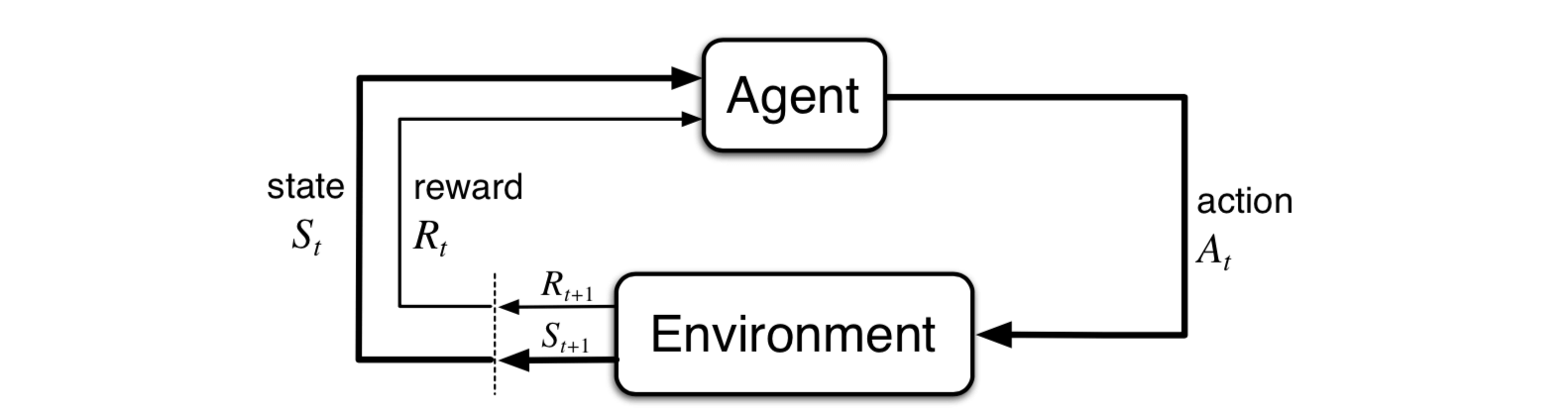
如上图所示,c和环境在离散时间序列每一步相互作用,t=0,1,2,3,…{t=0,1,2,3,…}t=0,1,2,3,…,对每个时间步t{t}t,智能体接收环境状态St∈S{S_t∈S}St∈S,并在此基础上选择一个动作At∈S(s){A_t∈S(s) }At∈S(s),智能体会接收到一个奖励值Rt+1∈R⊂R{R_{t+1}∈R⊂\R}Rt+1∈R⊂R,并且自身处于一个新状态St+1{S_{t+1}}St+1, 智能体与环境交互将产生一个状态-动作-奖励序列:
S0,A0,R1,S1,A1,R2…
S_0,A_0,R_1,S_1,A_1,R_2…
S0,A0,R1,S1,A1,R2…
由于S,A,R{S,A,R}S,A,R都属于有限集,随机变量Rt{R_t}Rt和StS_tSt有明确定义的离散联合概率分布:
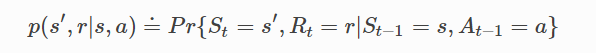
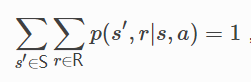
根据联合概率能依次求出状态转移概率(构成转移矩阵)、状态-动作预期奖励、状态-动作-下一状态预期奖励
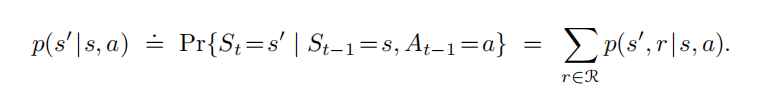
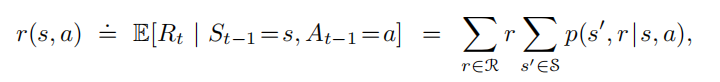
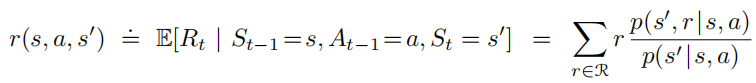
St{S_t}St和Rt{R_t}Rt的每个可能值的概率仅取决于前一个状态和动作St−1{S_{t−1}}St−1和At−1{A_{t−1}}At−1,认为状态具有马尔科夫性,可表示为:
Pss=P[St+1=s′∣St=s]
P_{ss}=P[S_{t+1}=s'|S_{t}=s]
Pss=P[St+1=s′∣St=s]
Goals and Rewards
- 使用奖励信号来形式化目标是强化学习最显着特征之一,奖励机制的合理设置对最终目标的实现至关重要。
- 奖励信号不是传授给智能体先验知识,不是仅仅教智能体完成奖励对应的动作,而是引导智能体通过学习完成最终目标。(例:国际象棋游戏中设置奖励是为了引导智能体学习如何获胜,而不是为了实现拿走对手的棋子或控制棋盘中心这样的子目标)
- 智能体的目标是最大化其收获的长期累积奖励。
Returns and Episodes
智能体尝试选择动作,以使其在未来接收的衰减的奖励的总和最大化。
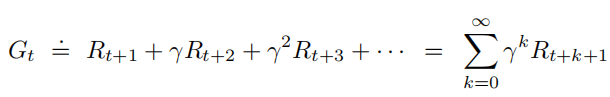
未来收到的k{k}k个时间步骤的奖励价值仅为立即收到的γk−1{γ^{k−1}}γk−1 倍。如果γ<1{γ<1}γ<1,只要奖励序列Rk{{R_k}}Rk有界,则上式一定收敛(收敛于Rmax1−γ{\frac{R_{max}}{1-\gamma}}1−γRmax)。 如果γ=0γ=0γ=0,智能体是短视的,只关注最大化立即奖励,在这种情况下,其目标是学习如何选择At{A_t}At以使Rt+1{R_{t+1}}Rt+1 最大化;当γ{γ}γ接近1时,回报目标更加强烈地考虑了未来的回报;智能体变得更有远见。
连续时间步骤的回报以递推式关联
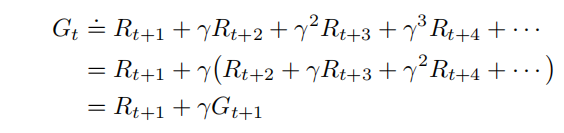
Unified Notation for Episodic and Continuing Tasks
常常不区分St{S_t}St和St,i{S_{t,i}}St,i(在情节i和时间t时的状态),其余同理。
考虑情节终止,可统一无限项的收益:进入一个特殊的吸收状态,该状态仅转换为自身并且仅产生零奖励。
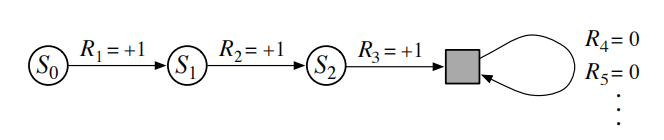
回报也可写成下式,包括T=∞或γ=1(但不能同时存在)的可能性。
Gt=∑k=t+1Tγk−t−1Rk
G_t=\sum^T_{k=t+1}\gamma^{k-t-1}R_k
Gt=k=t+1∑Tγk−t−1Rk
[Extensions to MDPs]
无限状态或连续 MDP;部分可观测 MDP;非衰减、平均奖励 MDP
Policies and Value Functions
策略是从状态到选择每个可能动作的概率的映射。
π(a∣s)=p[At=a∣St=s]
\pi(a|s)=p[A_t=a|S_t=s]
π(a∣s)=p[At=a∣St=s]
在状态s下,策略π下的c:
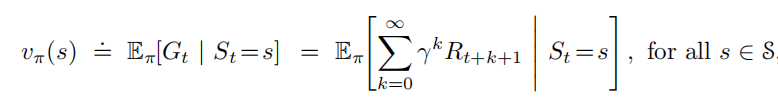
在状态s下,策略π下,采取动作a的行为值函数:
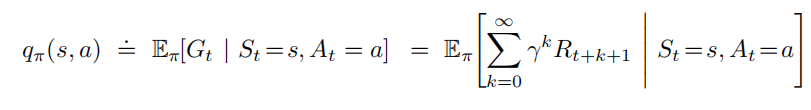
值函数与行为值函数具有如下关系:
vπ(s)=∑a∈Aπ(a∣s)qπ(s,a)
v_\pi(s)=\sum_{a\in A}\pi(a|s)q_π(s,a)
vπ(s)=a∈A∑π(a∣s)qπ(s,a)
【求值函数的思路】
-
动态规划方法:递推关系,即贝尔曼方程,可通过价值迭代、策略迭代、Q 学习、Sarsa 等方法求解
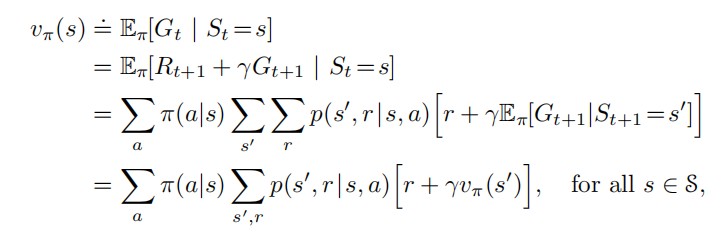
空心圆表示状态,实心圆表示状态-动作对。从状态s开始,顶部的根节点,智能体可以采取基于其策略π的任何一组动作,环境可以响应下一个状态中的其中一个s′以及产生奖励r,贝尔曼方程对所有可能性按概率进行加权平均。
-
蒙特卡洛方法:为每个状态采取的每项行动保留单独的累计回报G的平均值,它们将无偏地收敛于行动价值qπ(s,a){q_π(s,a)}qπ(s,a),但MC方法不能用于整个状态空间。
Optimal Policies and Optimal Value Functions
最优状态价值函数
v∗(s)=maxπvπ(s)for all s∈S
v_*(s)= \underset{\pi}\max v_\pi(s)\quad\quad \text{for all s}\in S
v∗(s)=πmaxvπ(s)for all s∈S
最优行为价值函数
q∗(s,a)=maxπqπ(s,a)for all s∈S
q_*(s,a)= \underset{\pi}\max q_\pi(s,a)\quad\quad \text{for all s}\in S
q∗(s,a)=πmaxqπ(s,a)for all s∈S
两者关系:
q∗(s,a)=E[Rt+1+γv∗(St+1)∣St=s,At=a]
q_*(s, a) = E[R_{t+1} + γv_*(S_{t+1}) | S_t =s, A_t =a]
q∗(s,a)=E[Rt+1+γv∗(St+1)∣St=s,At=a]
Optimality and Approximation
由于时间和内存的限制通常不可能通过求解贝尔曼最优方程来简单地计算最优策略,因此关键在于近似找到MDP问题的最优策略,为经常遇到的状态作出良好的决策,不用花费努力处理不经常遇到的状态。
Summary——Markov Decision Process
-
表示:<S,A,P,R,γ>
-
策略π(a∣s){\pi(a|s)}π(a∣s):表示给定状态下每个动作的概率分布,与时间无关,与历史无关
-
动作a下状态转移概率Pss′a{P_{ss'}^a}Pss′a,策略π{\pi}π下状态转移概率Pss′π=∑a∈Aπ(a∣s)Pss′a{P_{ss'}^\pi=\sum_{a\in A}\pi(a|s)P^a_{ss'}}Pss′π=∑a∈Aπ(a∣s)Pss′a
-
动作a下奖励Rsa{R_{s}^a}Rsa,策略π{\pi}π下奖励Rsπ=∑a∈Aπ(a∣s)Rsa{R_{s}^\pi=\sum_{a\in A}\pi(a|s)R^a_{s}}Rsπ=∑a∈Aπ(a∣s)Rsa
-
某状态s下策略π{\pi}π下值函数:vπ(s)=Eπ[Gt∣St=s]{v_\pi(s)=E_\pi[G_t|S_t=s]}vπ(s)=Eπ[Gt∣St=s]
-
某状态s下策略π{\pi}π下执行动作a动作值函数:qπ(s,a)=Eπ[Gt∣St=s,At=a]{q_\pi(s,a)=E_\pi[G_t|S_t=s,A_t=a]}qπ(s,a)=Eπ[Gt∣St=s,At=a]
-
Bellman 期望方程以及两者关系:
vπ(s)=Eπ[Rt+1+γvπ(St+1)∣St=s]qπ(s,a)=Eπ[Rt+1+γqπ(St+1,At+1)∣St=s,At=a]vπ(s)=∑a∈Aπ(a∣s)qπ(s,a) \begin{aligned} v_\pi(s)&=E_\pi[R_{t+1}+\gamma v_\pi(S_{t+1})|S_t=s]\\ q_\pi(s,a)&=E_\pi[R_{t+1}+\gamma q_\pi(S_{t+1},A_{t+1})|S_t=s,A_t=a]\\ v_\pi(s)&=\sum_{a\in A}\pi(a|s)q_π(s,a) \end{aligned} vπ(s)qπ(s,a)vπ(s)=Eπ[Rt+1+γvπ(St+1)∣St=s]=Eπ[Rt+1+γqπ(St+1,At+1)∣St=s,At=a]=a∈A∑π(a∣s)qπ(s,a) -
最优状态值函数&最优行为值函数:
v∗(s)=maxπvπ(s)for all s∈Sq∗(s,a)=maxπqπ(s,a)for all s∈S \begin{aligned} v_*(s)&= \underset{\pi}\max v_\pi(s)\quad\quad \text{for all s}\in S\\ q_*(s,a)&= \underset{\pi}\max q_\pi(s,a)\quad\quad \text{for all s}\in S \end{aligned} v∗(s)q∗(s,a)=πmaxvπ(s)for all s∈S=πmaxqπ(s,a)for all s∈S -
寻找最优策略

Chapter four: Dynamic Programming
动态规划用于在给定完整的环境模型是马尔可夫决策过程(MDP)的情况下计算最优策略的算法集合。
传统的DP算法在强化学习领域应用十分有限,因为它们不仅要求理想的模型,同时计算量也非常大,但也是非常重要的基础。
强化学习的核心思想是用价值函数去组织构建一种搜索从而找到好的策略,找到最优价值函数v∗{v_*}v∗或者q∗{q_*}q∗,就可以获得最优策略,即符合贝尔曼最优方程。而DP算法其实是将贝尔曼方程转换为更新规则以此来提升价值函数的近似效果。
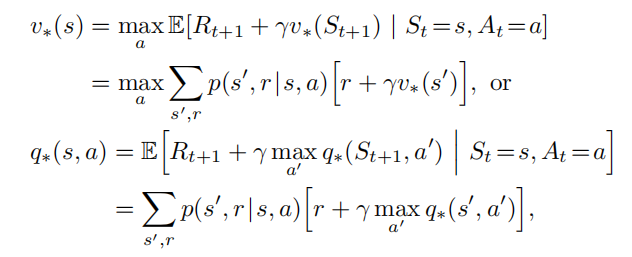
Policy Evaluation (Prediction)
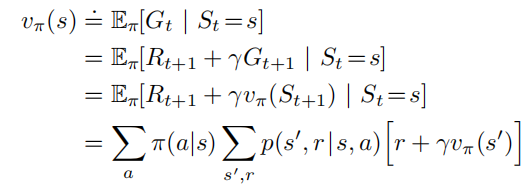
在环境已知(状态、回报、状态转移概率、折扣因子已知)的条件下该式可看作 |S|个线性方程与|S|个未知数的线性方程组,但状态空间很大时不易求解,因此考虑迭代法求解。值函数初值v0(s){v_0(s)}v0(s)任取,根据贝尔曼方程作为更新规则逐次逼近:
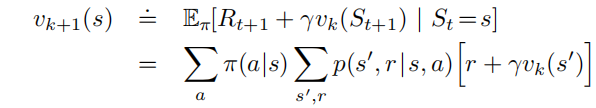
该算法即迭代策略评估,保证vπ{v_π}vπ的存在, 随着k→∞{k→∞}k→∞,vk{{v_k}}vk序列可以保证在广泛意义下收敛到vπ{v_π}vπ,vk=vπ{v_k=v_π}vk=vπ是这种更新规则下的不动点。
迭代策略评估伪码:

Policy Improvement
策略提升的核心思想:
在于找到在所有状态s选择执行一次动作a然后继续遵从策略π所得的行为值函数,该行为值函数满足qπ(s,π′(s))≥vπ(s){q_\pi(s,\pi'(s))\ge v_\pi(s)}qπ(s,π′(s))≥vπ(s),因此就有对所有状态s均满足vπ′(s)≥vπ(s){v'_\pi(s)\ge v_\pi(s)}vπ′(s)≥vπ(s)
[证明]
![image-20210925085915547]https://pic4.zhimg.com/80/v2-90445c5c718cb452fc9cf9a28d8935ed.png)
备注:π{\pi}π与π′{\pi'}π′除动作a其余一样
简单使用贪婪策略,就有:
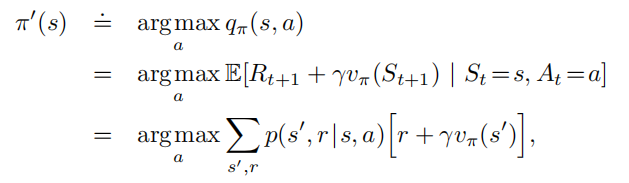
可以证明vπ′{v_{\pi'}}vπ′就是v∗{v_{*}}v∗,因此策略提升一定会得到一个不劣于当前策略的“更优策略”。
Policy Iteration
由策略π{\pi}π策略评估计算vπ{v_\pi}vπ再策略提升得到更好策略π′→{\pi'\rightarrow}π′→由策略π′{\pi'}π′策略评估计算vπ′{v_{\pi'}}vπ′再策略提升得到更好策略π′′{\pi''}π′′……以此类推可以得到一系列单调不减的策略和价值函数。
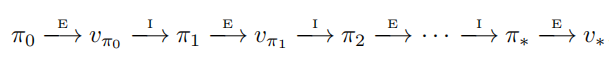
因为有限MDP只有有限个数量的策略,这个过程一定会在有限次的迭代中收敛到最优策略和最优价值函数。这种发现一个最优策略的方法叫做策略迭代,策略迭代完整的算法伪代码如下:

Value Iteration
策略迭代的缺点是:每一次迭代过程都包含策略评估,而策略评估本身需要多次对整个状态集迭代计算,且只能在极限处准确收敛到vπ{v_{\pi}}vπ。实际上,策略迭代过程中的策略评估可以在一次迭代之后就截断停止(每个状态只有一个回溯),该算法称作价值迭代 。价值迭代在更新过程中高效地结合了一轮策略评估更新和一轮策略提升更新,收敛更快,同时也可以证明值迭代不会失去收敛性,伪码如下:

Asynchronous Dynamic Programming
异步DP算法是就地迭代DP算法,并没有按照规则的状态集更新步骤进行组织,算法以任何顺序更新状态值,使用恰好可用的其他状态值,某些状态的值可能会在其他状态的值更新一次之前被更新多次。为了收敛到准确值,异步算法需要持续的回溯所有的状态值:在一定量的计算之后不能忽视任何状态。 异步DP算法在选择回溯更新状态时有极大的灵活性。
类似地,也可以混合策略评估和价值迭代回溯更新来生成一种异步截断策略迭代。
异步算法也使得与实时交互计算的结合更加容易。解决一个MDP问题,我们可以在智能体真正经历MDP的同时运行迭代DP算法。 智能体的经验可以用来决定DP算法将回溯更新应用到哪个状态上。同时,来自DP算法的最新值和策略信息可以用来指导智能体的决策。
Generalized Policy Iteration
广义策略迭代(GPI)指代策略评估和策略提升相互交互的一般概念,而不依赖于两个过程的颗粒度和其他细节。只要两个过程持续更新所有的状态,最终的结果就会一致,即收敛到最优价值函数和最优策略。几乎所有的强化学习方法都可以被描述为GPI。
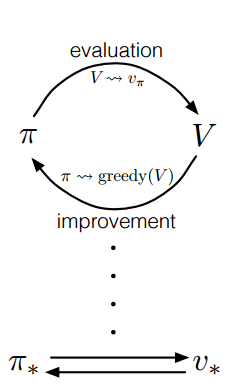
Efficiency of Dynamic Programming
DP方法保证能够在多项式时间内找到最优策略(对于n种状态和k个动作的系统,确定的策略总数是kn{k^n}kn),因为维度灾难才导致其应用受限。在大状态空间的问题上,由于在寻找最优解的过程中只可能有一小部分状态出现,因此异步方法和其他GPI的一些变种方法可以得到应用,并且可能比同步方法更快地找到好的或者最优的策略。
Summary
- 策略评估(以 n 次循环为单位):目的是为了得到好的 v(s){v(s)}v(s)。在当前π{ \pi}π下,对所有state,持续递推直至收敛。
- 策略改进(以 1 次循环为单位):目的是找到当前 v(s){v(s)}v(s)评估下的一个至少不会更差的策略(π′>π{\pi'>\pi}π′>π)
- 策略迭代循环进行策略评估和策略改进,时间主要花费在策略评估上(复杂问题的 states 会有很多,收敛较慢),因此引入了一次策略评估截断的价值迭代
- 策略迭代与值迭代的直观比较:
| 策略迭代 | 值迭代 |
|---|---|
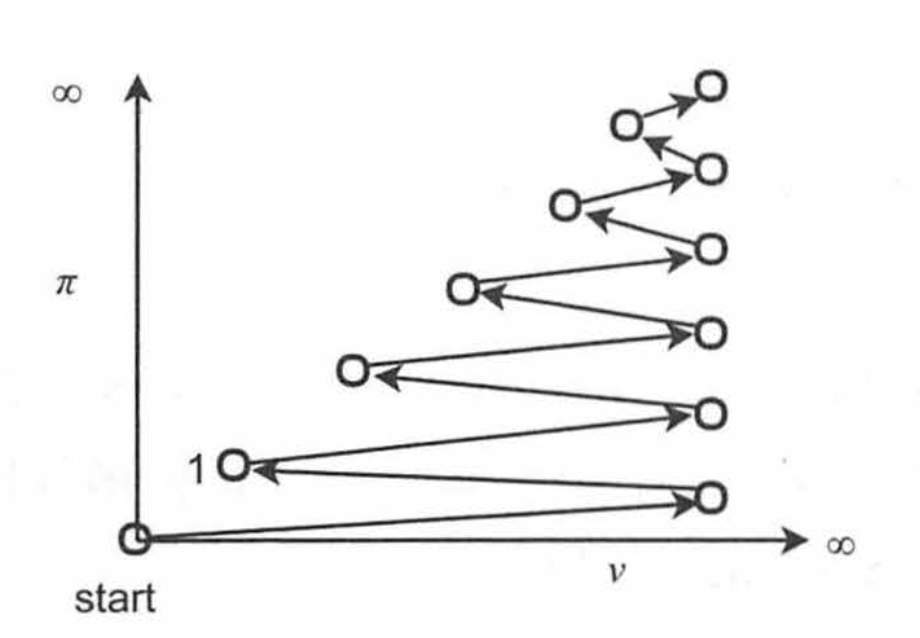 | 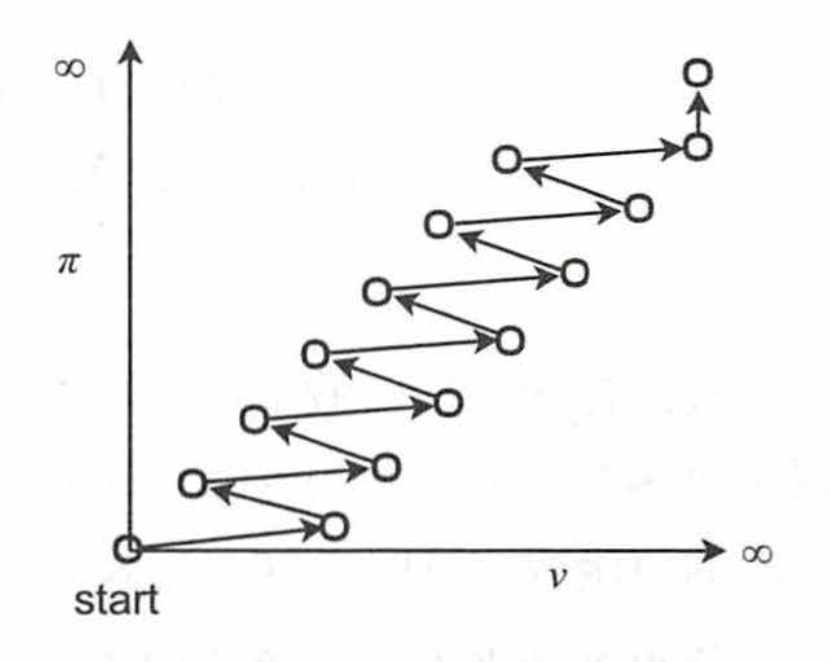 |
Chapter five: Monte Carlo Methods
在我们对环境不具备完全的了解的前提下,蒙特卡洛方法仅仅需要经验──与环境进行“真实”的或者“模拟”的交互所得到的状态、动作、奖励的样本序列,基于对样本回报求平均得到最佳策略。“真实”的经验学习不需要关于环境动态的先验知识仍然能够获得最优的行为(策略);模拟的经验学习需要一个概率模型仅用来产生样本。
Monte Carlo Prediction
在给定策略π{\pi}π的情况下,估计状态s{s}s的价值vπ(s){v_\pi(s)}vπ(s)有以下两种方法:
-
首次访问MC方法:所有回合中首次访问状态s{s}s的平均回报作为vπ(s){v_\pi(s)}vπ(s)的估计值
-
每次访问MC方法:所有回合中每次访问状态s{s}s的平均回报作为vπ(s){v_\pi(s)}vπ(s)的估计值方法同上,多一步检查在回合中早些时候是否发生过St{S_t}St
Monte Carlo Estimation of Action Values
已知模型的情况下,仅使用状态价值就可以决定策略(决定下一步只需要看哪个动作导致的奖励和下一状态组合最佳);未知模型情况下需清楚估计状态和动作的值。
-
首次访问MC方法中,每个回合只计算最多一次状态s{s}s开始,做出动作a{a}a,之后遵循策略π{π}π所得到的期望回报;
-
每次访问MC方法中,每次访问状态-动作对都会计算,最后求平均
然而,会有许多(s,a){(s,a)}(s,a)对从未被访问到,因此需用探索开端的方法:从特定的(s,a){(s,a)}(s,a)对出发,对每种动作都有大于零的概率选择到,探索开端能够保证经历无限个回合后,所有(s,a){(s,a)}(s,a)对都会被访问到无限次。更加普遍的一种方法是:选择随机策略,在每个状态下选择任意动作的概率都不为零。
策略提升的方法是贪婪地选择动作-价值函数最大的动作。
π(s)=arg maxaq(s,a)
\pi(s)={\underset {a}{\operatorname {arg\,max}}}q(s,a)
π(s)=aargmaxq(s,a)
【证】
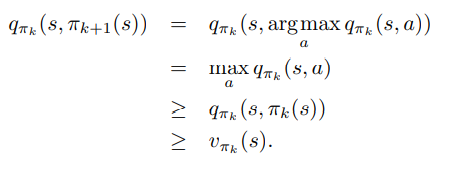
Monte Carlo Control
继承广义策略迭代(GPI)的思想,维持一个近似的策略和一个近似的价值函数,两者相互影响,任意一方的改变都会引起另一方的改变,使策略和价值函数都趋向于最优。
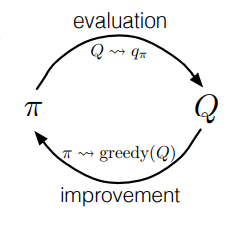
经典的蒙特卡洛方法策略迭代:交替执行策略迭代和策略提升,从一个随机的策略开始,以最优策略和最优的动作-价值函数结束:
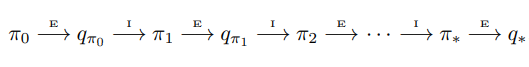
这需要两个极端的假设条件:①回合都是探索开端的方式;②有无限个回合供策略评估使用。解决第二个假设提出探索开端的蒙特卡洛算法:每一个回合结束后,观察到的回报用来做策略评估,然后对每个经历的状态做策略提升。

Monte Carlo Control without Exploring Starts
以一些游戏为例,难以任意初始状态,因此提出,提出非探索开端的蒙特卡洛控制。保证无限次后所有的动作都能被选到的惟一的通用办法是让智能体能够持续地选择它们,引入on-policy和off-policy方法。
** on-policy**:采样策略与评估策略是同种soft策略。
soft策略即π(a∣s)>0∀s∈S,a∈A{\pi(a|s)>0\quad\forall s\in S,a\in A }π(a∣s)>0∀s∈S,a∈A
最常见的ϵ−soft{ϵ−soft}ϵ−soft策略策略是ϵ−greedy{ϵ−greedy}ϵ−greedy策略(在ϵ−soft{ϵ−soft}ϵ−soft中,对所有的状态和动作, 有 π(a∣s)≥ϵ∣A(s)∣{π(a|s)≥\frac{ϵ}{|A(s)|}}π(a∣s)≥∣A(s)∣ϵ,ϵ−greedy{ϵ−greedy}ϵ−greedy策略是ϵ−soft{ϵ−soft}ϵ−soft中最接近贪心的)。
π(a∣s)={1−ϵ+ϵ∣A(s)∣if a=arg maxa q(a)ϵ∣A(s)∣if a≠arg maxa q(a)
π(a|s)=
\left\{
\begin{matrix}
1-\epsilon+\frac{ϵ}{|A(s)|} \quad \text{if }a=
{\underset {a}{\operatorname {arg\,max} }}\,q(a)\\
\frac{ϵ}{|A(s)|} \quad\quad\quad\quad \text{if }a\ne
{\underset {a}{\operatorname {arg\,max} }}\,q(a)
\end{matrix}
\right.
π(a∣s)=⎩⎨⎧1−ϵ+∣A(s)∣ϵif a=aargmaxq(a)∣A(s)∣ϵif a=aargmaxq(a)
on-policy MC的思想仍然是广义策略迭代,不断向贪心策略靠近即可。使用首次访问蒙特卡洛方法来估计当前策略的动作值函数,由于没有探索开端,我们不能简单地使用贪心来提升当前的策略。on-policy方法会不断的趋向于ϵ−greedy{ϵ−greedy}ϵ−greedy策略。 对任意的 ϵ−soft{ϵ−soft}ϵ−soft策略π{\pi}π,qπ{q_\pi}qπ对应的任意的ϵ−greedy{ϵ−greedy}ϵ−greedy都不坏于策略π{\pi}π,证明策略改进如下:
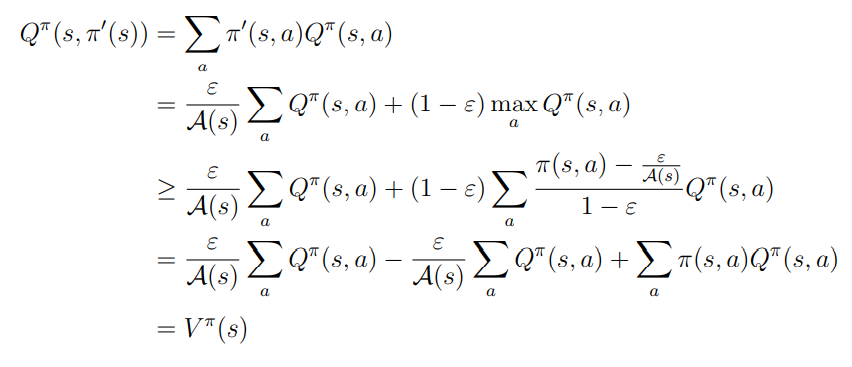
on-policy MC算法流程如下:

Off policy Prediction via Importance Sampling
** off-policy**:行为策略是soft policy而目标策略不一定,使用行为策略π′{\pi'}π′估计目标策略π{\pi}π,前提是在π{\pi}π下采取的动作在π′{\pi'}π′下也发生过,即:
∀π(a∣s)>0π′(a∣s)>0
\forall \pi(a|s)>0\quad\pi'(a|s)>0
∀π(a∣s)>0π′(a∣s)>0
pi(s),pi(s)′{p_i(s),p_i(s)'}pi(s),pi(s)′分别表示π,π′{\pi,\pi'}π,π′下从状态s{s}s开始产生一段序列的联合概率,由于sk{s_k}sk通过动作ak{a_k}ak转移到sk+1{s_{k+1}}sk+1的概率与策略无关比值消掉,有:
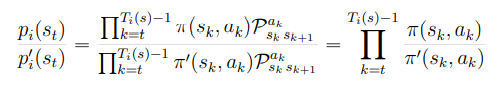
重要性采样推导:

ns{n_s}ns条链加权重要性采样(归一化,避免pi(s)pi(s)′{\frac{p_i(s)}{p_i(s)'}}pi(s)′pi(s)绝对大小过大的影响):
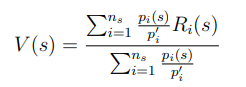
Incremental Implementation(增量式实现)
多臂赌博机中平均奖励,蒙特卡洛方法中平均回报,同样可用增量式编程实现
初始,从状态s开始的一系列回报值G1,G2,…Gn{G_1,G_2,…G_n}G1,G2,…Gn,Gi{G_i}Gi对应一个随机的权值Wi{W_i}Wi。每获得一个额外的回报Gn{ G_n}Gn时,Wn{W_n}Wn由重要性权重迭代,Cn{C_n}Cn记录前n个回报下每个状态的累积权值,更新Vn{V_n}Vn,规则如下:
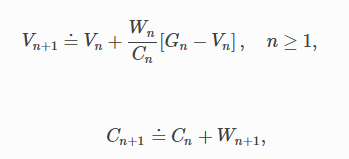
Off policy Monte Carlo Control


Discounting-aware Importance Sampling
之前讨论的离策略是基于重要性采样,将回报看成一个整体,对回报进行加权, 并没有考虑到回报内在的结构是折扣奖励的和。 现在使用折扣奖励的结构来减少离策略估计的方差。
平坦部分回报
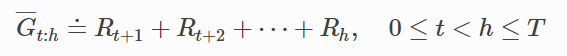
折扣感知加权重要性采样估计器
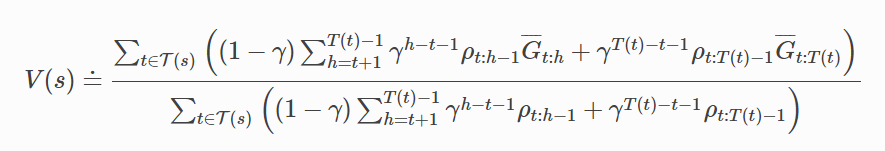
Per-decision Importance Sampling
在离策略重要性采样里将回报结构作为奖励总和考虑在内, 这样即使在没有折扣的情况下(即γ=1)也可以减少方差。
per-decision重要性采样
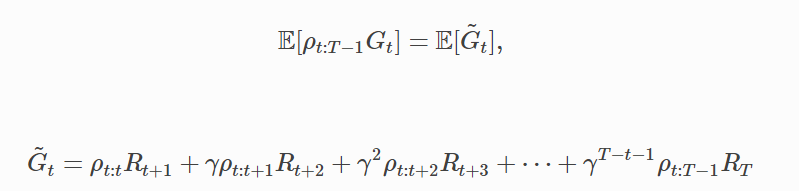
交替重要性采样估计器(无偏)
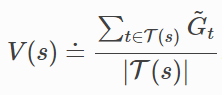
Summary
蒙特卡洛方法以样本回合的方式,从经验中学习价值函数和最优策略。相比DP方法有三种优势:
-
直接从与环境的交互中学习到最优的行为,并不需要知道环境的动态。
-
能够被用于模拟或样本模型。在难以建立具体的转移概率的模型 (DP方法必须)情况下可以很容易去估计样本回合。
-
很容易且很有效率地聚焦到状态的小子集。 对于我们特别感兴趣的区域,可以准确地评估,而不需要费大力气去准确地评估剩余的状态集。
-
对于违反马尔可夫过程的行为会受到更少的伤害,因为不用自举bootstrap。
MC方法遵循广义策略迭代(GPI)的整体架构,包含了策略评估和策略迭代的交互过程。MC策略评估回归定义,状态的价值就是从该状态开始得到的回报的期望,采取从该状态开始得到的回报求平均的办法而不是使用模型去计算每个状态的价值。同理计算行为值函数提升策略,无需知道环境转移动态。MC方法以回合制的方式混合了策略评估和策略提升,而且可以以回合制的方式增量地实现。
蒙特卡洛控制方法中的一个重要问题是保持有效的探索。仅仅选择当前估计的最好动作是不够的,因为这样不能得到其他动作的回报而且不能学习到更好的策略。因此可采取:
- 探索开端:随机地选择状态-动作对,以覆盖所有的可能
- 非探索开端:on policy智能体会不断探索策略,优化的策略仍然保持探索;off policy智能体会不断探索,但是会学习一个与该策略无关的确定性的最优策略。
离策略预测基于重要性采样(用两种策略下执行观察到的动作的可能性的比值加权回报),从一个不同的行为策略产生的数据中学习一个目标策略。
- 原始重要性采样使用加权回报的简单平均,无偏估计,但方差大
- 加权重要性采样使用加权平均,方差有限
MC方法与DP方法有两个主要的不同点:
-
MC对样本经验进行操作,因此可以不用模型直接进行学习。
-
没有提升(bootstrap),不依赖其他的价值估计来更新自己的价值估计。
引入TD时间差分的方法综合两者特点。
Chapter six: Temporal-Difference Learning
TD学习是蒙特卡洛思想和动态规划思想的结合。与蒙特卡洛方法一样,TD方法可以直接从原始经验中学习,而无需环境动态模型。 与DP一样,TD方法部分基于其他学习估计更新估计(自举)。
TD Prediction
constant-alpha MC
V(St)←V(St)+α[Gt−V(St)]
V(S_t)\leftarrow V(S_t)+\alpha[G_t-V(S_t)]
V(St)←V(St)+α[Gt−V(St)]
蒙特卡罗方法必须等到回合结束,才能根据已知的Gt{G_t}Gt确定V(St){V(S_t)}V(St)的增量;而TD方法需要t+1{t+1}t+1使用观察到的奖励Rt+1{R_{t+1}}Rt+1进行更新,其中中括号部分是TD误差。**TD(0)**公式及算法如下。由于TD(0)部分基于现有估计进行更新,所以称其为自举(bootstrapping)的方法。
V(St)←V(St)+α[Rt+1+γV(St+1)−V(St)]
V(S_t)\leftarrow V(S_t)+\alpha[R_{t+1}+\gamma V(S_{t+1})-V(S_t)]
V(St)←V(St)+α[Rt+1+γV(St+1)−V(St)]

[备注]
若V在回合期间没有改变(或变化很小),蒙特卡罗误差可以近似写成TD误差的和
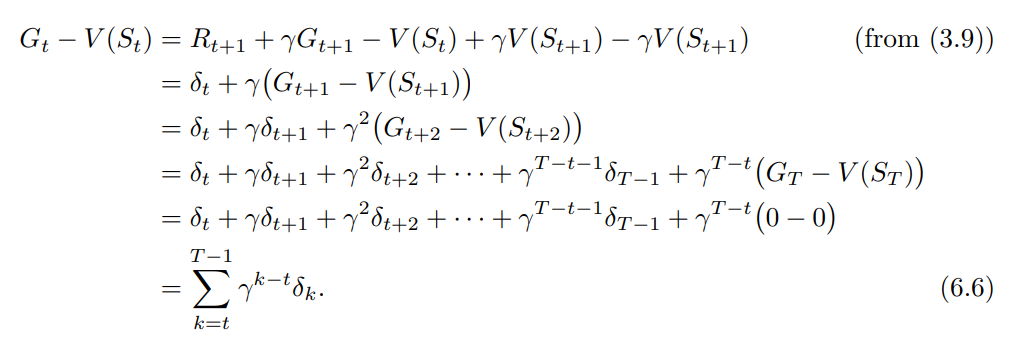
- 对MC/DP/TD是“估计”的理解:
- MC:vπ(s)=Eπ[Gt∣St=s]{v_\pi(s)=E_\pi[G_t|S_t=s]}vπ(s)=Eπ[Gt∣St=s],使用样本回报来代替实际预期回报
- DP:vπ(s)=Eπ[Rt+1+γvπ(St+1)∣St=s]=⋅Eπ[Rt+1+γV(St+1)∣St=s]{v_\pi(s)=E_\pi[R_{t+1}+\gamma v_\pi(S_{t+1})|S_t=s]\stackrel{\mathrm{·}}{=}E_\pi[R_{t+1}+\gamma V(S_{t+1})|S_t=s]}vπ(s)=Eπ[Rt+1+γvπ(St+1)∣St=s]=⋅Eπ[Rt+1+γV(St+1)∣St=s],使用V(St+1){V(S_{t+1})}V(St+1)代替vπ(St+1){v_\pi(S_{t+1})}vπ(St+1)
- TD:采样预期值;使用当前估计值V{V}V而不是真实vπ{v_\pi}vπ
Advantages of TD Prediction Methods
MC方法必须等到回合结束,减慢学习速度;TD方法只需等待一个时间步,无论后续采取何种行动,它都会从紧邻的下一个转变中学习。
π′≥π\pi'\ge\piπ′≥π,即∀s,Vπ′(s)≥Vπ(s)\forall s,V^{\pi'}(s)\ge V^{\pi}(s)∀s,Vπ′(s)≥Vπ(s)的证明
Optimality of TD(0)
- 在批量更新中,TD(0)确定性地收敛到与步长参数α{\alpha}α无关的单个答案,只要选择α{\alpha}α足够小。 α−{\alpha-}α−MC方法也在相同条件下确定性地收敛,但是收敛到不同的案。
- 批量蒙特卡罗方法总是找到最小化训练集上的均方误差的估计, 而批量TD(0)总是找到对马尔可夫过程的最大似然模型完全正确的估计。
- 批量TD(0)收敛于确定性等价估计。具有大状态空间的任务中,TD方法可能是近似确定性等价解的唯一可行方法。
Sarsa: On-policy TD Control
(St,At,Rt+1,St+1,At+1){(S_t,A_t,R_{t+1},S_{t+1},A_{t+1})}(St,At,Rt+1,St+1,At+1)五元组构成Sarsa的核心。若St+1{S_{t+1}}St+1是终点,Q(St+1,At+1)=0{Q(S_{t+1},A_{t+1})=0}Q(St+1,At+1)=0。 从一个状态-动作对到下一个状态-动作对的转换按如下公式:
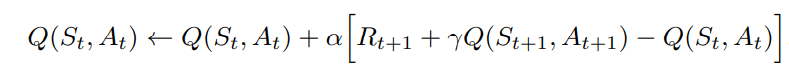
Sarsa算法的收敛属性取决于策略对Q的依赖性。只要所有状态-动作对被无限次访问并且策略收敛于贪婪策略 (例可以控制ε=1/t),Sarsa就一定收敛到最优策略和动作-价值函数。
Sarsa算法如下:

Q-learning: Off-policy TD Control
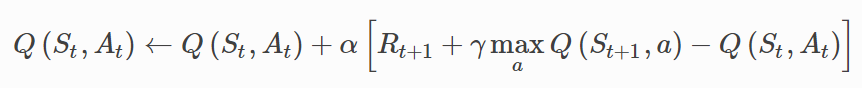
异策略Q−learning{Q-learning}Q−learning学习的动作-价值函数Q直接近似最佳动作-价值函数q∗{q_∗}q∗,与所遵循的策略无关,策略是用来确定访问和更新哪些状态-动作对,也需要具备所有动作-价值对都能持续更新的要求。

Expected Sarsa
期望Sarsa可被认为遵循Q-learning的异策略,区别在于其考虑到当前策略下每个动作的可能性,使用预期值而不是最大化下一个状态-动作对。给定下一个状态St+1S_{t+1}St+1,算法确定地在与Sarsa期望移动的方向相同的方向上移动。
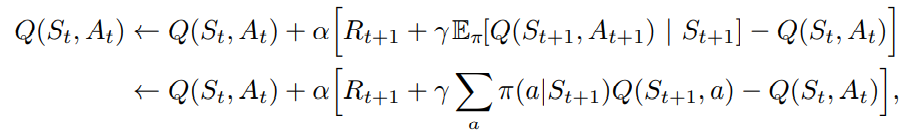
Maximization Bias and Double Learning
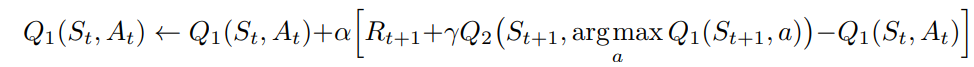

Games, Afterstates and Other Special Cases
像井字棋游戏中agent{agent}agent学习到的是afterstate{afterstate}afterstate价值函数(采取动作后使用状态价值函数评估棋盘位置)。当我们了解环境动态的初始部分但不一定了解完整的动态时afterstates{afterstates}afterstates表现很好。对不同的(St,At){(S_t,A_t)}(St,At)转移到相同的(St+1,At+1){(S_{t+1},A_{t+1})}(St+1,At+1)的情况afterstate{afterstate}afterstate价值函数将同等地评估两个对而传统的行动-价值函数则会分别评估。
Summary
构成GPI的两大部分:
- 用价值函数准确地预测当前策略的回报,这是预测问题。TD方法是用于解决预测问题的蒙特卡罗方法的替代方法,想法是近似策略和价值函数应该以朝着最优价值方向移动。注意保持足够的探索。
- 推动策略对于当前价值函数在局部地进行改进,这是控制问题
Sarsa是一种同策略的方法,而Q-learning是一种异策略的方法,期望Sarsa也是一种异策略的方法,第三种方法可以扩展TD方法来控制。
Chapter nine: On-policy Prediction with Approximation
函数近似方法中,近似值函数不是用表格表示, 而表示成是具有权重向量 w∈Rdw∈\R^dw∈Rd的参数化函数形式,v^(s,w)≈vπ(s)\hat v(s,w)≈v_π(s)v^(s,w)≈vπ(s)。$\hat v 可能是状态特征中的线性函数,可能是状态特征中的线性函数,可能是状态特征中的线性函数,w是特征权重的向量。更一般地,是特征权重的向量。 更一般地,是特征权重的向量。更一般地,\hat v 可以是由多层人工神经网络计算的函数,其中可以是由多层人工神经网络计算的函数,其中可以是由多层人工神经网络计算的函数,其中w是所有层中的连接权重的向量,通过调整权重,网络可以逼近任何函数。通常,权重的数量(是所有层中的连接权重的向量,通过调整权重,网络可以逼近任何函数。通常,权重的数量(是所有层中的连接权重的向量,通过调整权重,网络可以逼近任何函数。通常,权重的数量(w的维数)远小于状态的数量的维数)远小于状态的数量的维数)远小于状态的数量(d≪|S|)$, 并且改变一个权重会改变许多状态的估计值。因此,当更新单个状态时,更改会从该状态推广到许多其他状态的值,这种泛化使得学习可能更强大。
Value-function Approximation
强化学习能够在线进行,需要能够从增量获取的数据中有效学习的方法,也通常需要函数近似方法能够处理非平稳目标函数(随时间变化的目标函数)。
The Prediction Objective (VE)
表格学习中学习价值函数可以精确地等于真值函数,且每个状态的学习价值都是分离的──一个状态的更新不受其他影响。 但是函数近似中,一个状态的更新会影响许多其他状态,并且不可能使所有状态的值完全正确(状态数量>权重数量)。我们通过MSE关心每个状态sss中的“错误程度”,
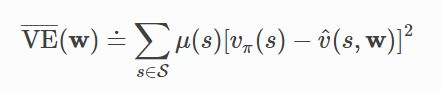
总结:用于将价值预测的各种强化学习方法与各种函数近似方法相结合,使用前者的更新为后者生成训练样本,理想的目标是找到一个全局最优值,VE‾(w∗)≤VE‾(w)\overline {VE}(w^*)\le \overline {VE}(w)VE(w∗)≤VE(w)。
Stochastic-gradient and Semi-gradient Methods
SGD随机梯度下降方法通过在每个采样之后将权重向量最大程度地向损失函数VE‾{\overline {VE}}VE降低的方向少量调整来实现:

解释SGD在梯度降低方向改变一小步而非一直移动直到完全消除误差:
我们不会寻找或期望找到一个对所有状态都没有误差的价值函数, 而只是一个平衡不同状态误差的近似值,若在一个步骤中完全纠正每个样例,那就找不到这样的平衡。
一般SGD方法用于状态价值预测公式如下。在UtU_tUt是无偏估计的情况下(即∀t,E[Ut∣St=s]=vπ(St)\forall t,E[U_t|S_t=s]=v_π(S_t)∀t,E[Ut∣St=s]=vπ(St),如蒙特卡洛目标中Ut≐GtU_t≐G_tUt≐Gt,GtG_tGt是vπ(St)v_π(S_t)vπ(St)的无偏估计),则 wtw_twt保证对于α在通常的随机近似条件下收敛到局部最优值。一般SGD方法收敛于 vπ(St)v_π(S_t)vπ(St)的局部最佳近似。
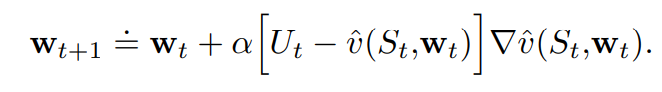
梯度下降蒙特卡洛算法如下:

注意使用n步回报 Gt:t+nG_{t:t+n}Gt:t+n或者TD目标等自举目标估计UtU_tUt不可行,因为上式中对损失函数求导是默认vπ(St)v_π(S_t)vπ(St)不是w的函数,因此提出了半梯度下降。使用半梯度下降既显着加快学习速度又使学习能够连续和在线,而无需等待回合的结束。一种原型半梯度方法是半梯度TD(0),使用Ut≐Rt+1+γv^(St+1,w)U_t≐R_{t+1}+γ\hat v(S_{t+1},w)Ut≐Rt+1+γv^(St+1,w)作为目标,算法如下:

Linear Methods
函数近似的一个最重要的特殊情况是其中近似函数v^(⋅,w)\hat v(⋅,w)v^(⋅,w)是权重向量w的线性函数。其中x(s)被称为表示状态s的特征向量,xi:S→Rx_i:S→Rxi:S→R。
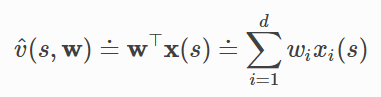
随机梯度下降更新:
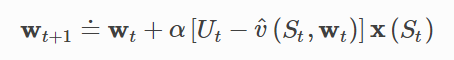
线性SGD情况简单,最有利于数学分析,几乎所有类型的学习系统的有用收敛结果都是线性(或简单)函数近似方法。在线性情况下,只有一个最优(或者,在简并情况下,一组同样良好的最优),因此任何保证收敛到或接近局部最优的方法都会自动保证收敛到或接近全局最优。
半梯度TD(0)算法的线性函数近似,复杂度O(d)O(d)O(d)。
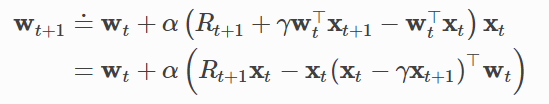
Feature Construction for Linear Methods
线性方法关键在用特征表示状态;线性方法保证收敛,但是限制在于不能考虑特征之间的任何相互作用(如在倒立摆问题中高角度下的高角速度为危险而低角度下的高角速度为良好,对两状态特征单独编码的情况下线性方程不能表示该特点)。解决该问题的方法是加入状态维度的组合的特征,可通过使用多项式/傅立叶基/粗编码/铺片编码/径向基函数。
Selecting Step-Size Parameters Manually
大多数SGD方法都要求手动设置合适的步长参数ααα,在表格MC方法中产生样本平均值的经典选择$ α_t=1/t$不适用于TD方法、非平稳问题或任何使用函数近似的方法。
一般来说,如果α=1/τα=1/τα=1/τ,那么一个状态的表格估计在关于状态的τ次经验后将接近其目标的均值,目标效果最好。对于一般函数的近似,没有关于状态的经验数量这种明确概念,因为每个状态可能与所有其他状态在不同程度上相似和不相似。在线性函数近似的情况下,想在τ个经验内用大致相同的特征向量来学习,可按如下经验法则。其中,x是从与SGD中的输入矢量相同的分布中选择的随机特征向量,如果特征向量的长度变化不大,则此方法效果最佳;理想情况下,x⊤xx^⊤xx⊤x是常数。
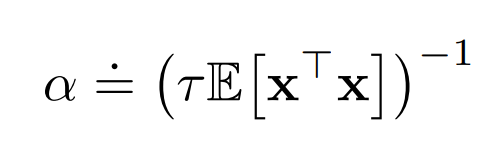
Nonlinear Function Approximation: Artificial Neural Networks
核心:
- 激活函数:S形曲线或整流非线性relu
- 优化方法:随机梯度法,反向传播
- 监督学习:RL中标签可选取TD误差/最大化预期奖励
深层网络问题:
- 深层网络易过拟合(未能正确地泛化到网络未训练过的情况)
- 深层网络难反向传播(梯度消失/梯度爆炸)
减少过拟合方法:
-
交叉验证
-
正则化
-
权重共享
-
dropout
-
深度信念网络
-
批量标准化
-
深度残差学习
-
深度卷积网络(处理以空间阵列(如图像)排列的高维数据)
Least-Squares TD
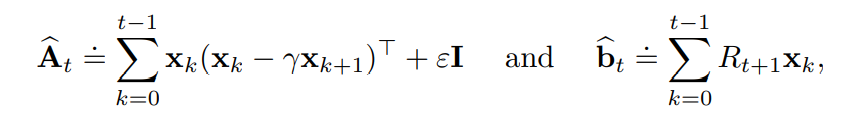
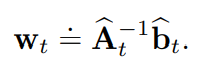
LSTD算法是线性TD(0)的最具数据效率的形式,其中逆矩阵运算可以用逐步更新的方式将时间复杂度从一般的O(d3)O(d^3)O(d3)降低到O(d2)O(d^2)O(d2),d为权重数。
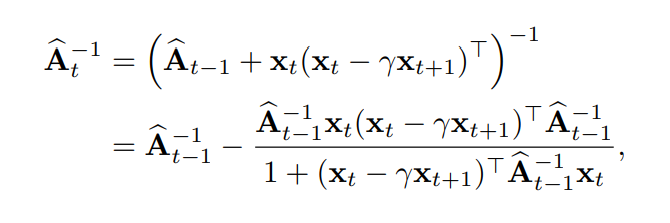
LSTD时间空间复杂度都是O(d2)O(d^2)O(d2),算法流程如下:

LSTD中如果εεε选择得太小,逆的序列可能变化很大,如果εεε选择得太大,那么学习速度会慢。
Memory-based Function Approximation
基于内存的函数近似方法是非参数方法的主要示例,将训练样例保存在内存中(或者至少保存一部分样例)而不更新任何参数。每当需要查询状态的价值估计时,从内存检索一组样例并用于计算查询状态的价值估计。因为处理训练样例被推迟,直到查询系统以提供输出,该方法有时被称为延迟学习。基于内存的函数近似方法不限制对预先指定的函数形式的近似。 随着更多数据的累积,这可以提高准确性。
与参数方法不同,近似函数的形式不限于固定的参数化函数类, 例如线性函数或多项式,而是由训练样本本身确定,以及将它们组合到输出查询状态的估计值的一些方法。局部学习(local-learning)方法仅在当前查询状态的邻域中本地近似价值函数,从内存中检索一组训练样例,其状态被判断为与查询状态最相关,其中相关性通常取决于状态之间的距离。在给查询状态赋值之后,丢弃局部近似。举例有最近邻方法、加权平均方法、局部加权回归方法。
Kernel-based Function Approximation
基于记忆的方法中需要分配一个一般和距离成反比的权重,这个权重由的核函数(kernel function)决定。
核函数是一个映射 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vZdd5fD9-1646808434797)(https://www.zhihu.com/equation?tex=k%3A%5Cmathcal%7BS%7D+%5Ctimes+%5Cmathcal%7BS%7D+%5Cmapsto+%5Cmathbb%7BR%7D)] 。将两个状态映射成一个实数。这个实数的大小则反映了这两个状态的相关性。核函数 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-f0dfyuZW-1646808434798)(https://www.zhihu.com/equation?tex=k%28s%2Cs%27%29)] 表达了从状态 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-0zz1vrdC-1646808434799)(https://www.zhihu.com/equation?tex=s%27)] 到 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-eyZaJ8Xm-1646808434799)(https://www.zhihu.com/equation?tex=s)] 泛化强度的度量。是一种很广泛的泛化机制。
核回归就是一种基于记忆的核加权均值方法。假设 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Ma93TTcO-1646808434800)(https://www.zhihu.com/equation?tex=%5Cmathcal%7BD%7D)] 是存储的样本, [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-A5fbHTYX-1646808434800)(https://www.zhihu.com/equation?tex=g%28s%27%29)] 表示 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ICLJ0dr1-1646808434801)(https://www.zhihu.com/equation?tex=%5Cmathcal%7BD%7D)] 某个状态 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-snnIhzUz-1646808434801)(https://www.zhihu.com/equation?tex=s%27)] 的目标值。核回归通过下面的公式近似目标函数。其中 k(s,s′)k(s,s′)k(s,s′)仅在sss和s′s's′彼此接近时才为非零。
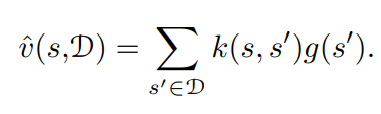
任何线性回归参数方法,在把状态被表示成一个特征向量![[公式]](https://i-blog.csdnimg.cn/blog_migrate/e888ba73257afe063e2cd36c255d32d1.png) 的情况下,总是能等价为一个核回归问题,而且核函数就等于特征向量的内积:
的情况下,总是能等价为一个核回归问题,而且核函数就等于特征向量的内积:
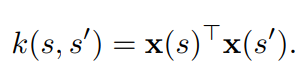
Looking Deeper at On-policy Learning: Interest and Emphasis

DQN的几种改进trick
-
Double DQN:TD目标中将maxQtarget→Qtarget(st,argmaxQbehavior(st,a))\max Q_{target}\to Q_{target}(s_t,\arg\max Q_{behavior}(s_t,a))maxQtarget→Qtarget(st,argmaxQbehavior(st,a)),改善过优选择的问题
-
Dueling DQN:在DQN的基础上仅改善了网络架构,不是仅输出Q(s,a)关于a的向量而是输出Q(s,a)=标量V(s)+向量A(s,a),其中向量A(s,a)去中心化(网络中对输出的A(s,a)加一层操作Aˉ(s,a)=A(s,a)−mean(A(s,a))\bar A(s,a)=A(s,a)-mean(A(s,a))Aˉ(s,a)=A(s,a)−mean(A(s,a)))使元素和为0从而保证V(s)是Q(s,a)的均值,这样不用采样每个(s,a)对而仅通过改变V(s)就能通过广播加法Q(s,a)=V(s)+A(s,a)完成对每个可能未采样到的Q(s,a)的更新。
-
Prioritized Replay:对TD误差大的(st,at,rt,st+1)(s_t,a_t,r_t,s_{t+1})(st,at,rt,st+1)交互优先回放更新网络参数
-
Muti-step:将TD目标改成TD(λ)方差小于MC偏差小于TD
-
Noisy Net:在每个回合开始前在Q网络的每个参数添加一个高斯噪声,该噪声在一回合中不会改变。相比e-greedy的策略,给定相同s下a可能会不一样,这种随机乱试不符合实际情况;而一回合内网络参数加噪声是固定的,对每个状态探索的随机性是一致的(Explore in a consistent way),对相同(相似)的状态会做出相同的动作(State-dependent Exploration)。
-
Distributional Q-function:Q网络中输入s,输出每个a处的值的一个分布信息(DQN可以理解成输出的是分布的期望/均值,一个特殊的数字特征),不过执行时还是利用均值选动作。C51就是将连续的Q取值范围离散成51个支集(support)。
备注:在使用值分布强化学习的时候往往不会出现TD目标overestimate的问题反而容易underestimate,因为离散化Q时肯定会有上下界,而超过界限的Q值就会被直接被忽略没有被选到的可能。所以在rainbow中拿掉DDQN影响不明显。
Summary
强化学习系统必须能够泛化,可将每个更新视为训练样例,使用监督学习函数近似的方法,其中最合适的是参数化函数近似的方法。将策略由权向量w参数化,定义均方值误差VE‾\overline {VE}VE为在策略分布μ下权重向量w的值$v_{π_w}(s) $中的误差的度量。为找到好的权重向量,使用随机梯度下降(SGD),采用n步半梯度TD(特殊情况包括梯度蒙特卡罗和半梯度TD(0)算法)。半梯度的理解是权重向量出现在更新目标中,但在计算梯度时不考虑。
线性函数近似的情况下,半梯度方法获得良好结果的关键是选取适当特征。它们可以被选择为多项式,但是这种情况在通常在强化学习中考虑的在线学习设置中很难感化。 更好的是根据傅立叶基选择特征,或者根据稀疏重叠感受域的某种形式的粗编码。 铺片编码是粗编码的一种形式,其特别具有计算效率和灵活性。 径向基函数对于一维或二维任务非常有用,其中平滑变化的响应很重要。LSTD是数据最有效的线性TD预测方法,相比其他复杂度均为O(d)O(d)O(d)方法其复杂度O(d2)O(d^2)O(d2)。非线性方法包括通过反向传播训练的人工神经网络,认为是深度强化学习的初期代表。
Chapter ten: On-policy Control with Approximation
之前涉及的都是动作价值方法,即必须了解动作的价值才能根据所估计的行动价值选择行动。而策略梯度方法参数化策略,可以不使用值函数选择动作。
Policy Approximation and its Advantages
策略梯度方法中要保证 π(a|s,θ) 相对于其参数可微,且要求策略永远不要具有确定性(即对于所有s,a,θ,有 π(a|s,θ)∈(0,1))。常使用指数soft-max分布使具有最高偏好的动作被赋予最高的选择概率,动作偏好本身可以由神经网络计算,其中 θ 是网络所有连接权重的向量。
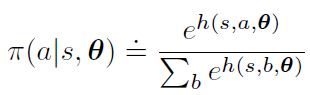
相比使用网络逼近值函数再使用e−greedye-greedye−greedy策略选择动作相比,soft-max动作偏好参数化策略的优点有:
- 近似策略可以接近确定性策略。soft−maxsoft-maxsoft−max动作偏好中网络训练出的h由于没有实际意义可以很大而使得ehe^heh逼近1,而值函数逼近中,若使用e−greedye-greedye−greedy策略则必然存在 ε 可能性选择随机动作;若使用玻尔兹曼分布则由于值函数的实际意义,不同动作之间的Q相差不大,soft−maxsoft-maxsoft−max后更接近均匀策略,更加难以接近确定性策略。
- 可以为每个动作分配任意概率,当最佳近似策略是随机时也可以训练出。
- 另外,使用基于策略的学习方法的最重要原因是可以注入先验知识
The Policy Gradient Theorem
参数化策略相对于e−greedye-greedye−greedy策略还有一个重要的理论优势:随着策略参数化的不断进行,动作概率将随着学习参数的变化而平稳变化,依赖于参数的连续性能够近似梯度上升;而在e−greedye-greedye−greedy策略中如果估计的动作值发生任意小的变化动作概率可能会发生显著变化,该变化还可能导致具有最大值的不同动作。策略梯度法比行动值函数法具有更强的收敛保证。
策略梯度定理证明:

REINFORCE: Monte Carlo Policy Gradient
随机梯度上升总体策略需要一种采样方法,使得样本梯度的期望值与作为参数函数的性能度量的实际梯度成正比(样本梯度只需与梯度成比例,因为任何比例常数都可以吸收到步长中)。策略梯度定理需要一种采样方法,保证样本期望值等于或近似于一个与梯度成正比的精确表达式。
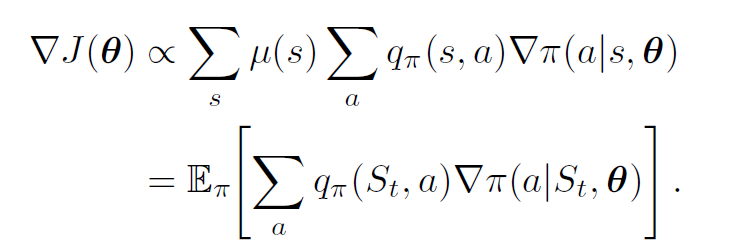
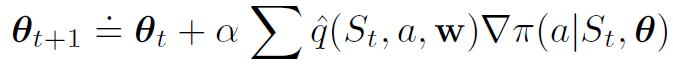 ↓
↓
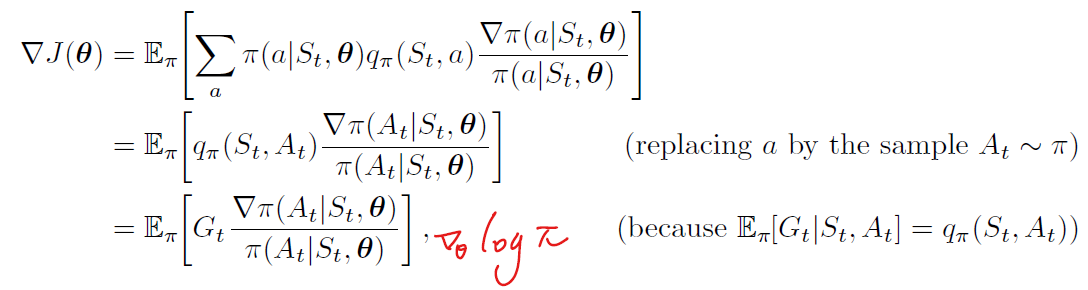
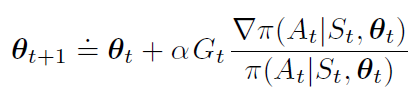
每个增量与返回Gt和向量的乘积成正比,实际采取行动的概率梯度除以采取行动的概率。向量是参数空间中的方向,该方向最大程度地增加了在未来访问状态StS_tSt时重复操作的概率。更新在该方向上增加的参数向量与返回成正比,使参数朝着有利于产生最高回报的操作的方向移动;与操作概率成反比,尽量多更新选择频率低的动作处的参数,减少遗漏最优动作的可能。
备注:伪代码最后一行∇lnx=∇xx\displaystyle \nabla lnx=\frac{\nabla x}{x}∇lnx=x∇x
蒙特卡洛REINFORCE方法仅适用于完整采样episode的情况,使用一个episode的完整折扣累计回报在一个episode结束后进行更新。

REINFORCE作为一种随机梯度法,具有良好的理论收敛性。通过构造,在一个episodec中预期的更新与参数梯度的方向相同。这可确保在足够小的时间内提高预期性能, 并在标准随机逼近条件下收敛到局部最优。然而,作为一种蒙特卡罗方法,它可能具有高方差,因此学习缓慢。
REINFORCE with Baseline
baseline是一个与动作a无关的函数,基线的加入可以保证目标函数J的均值不变而方差减少。带有基线的策略梯度更新和期望不变证明如下:
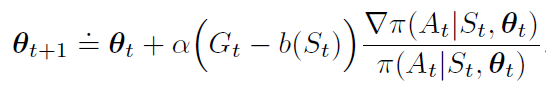
在一些状态下所有的动作都有很高的值,我们需要一个很高的基线区分价值较高的行为与价值较低的行为;在其他状态下,所有动作都具有低值,低基线是合适的。一种基线的选择是估计状态值函数v^(st,w)\hat v(s_t,w)v^(st,w)(与a无关),很自然使用蒙特卡罗方法来学习状态值权重w。使用基线的蒙特卡洛REINFORCE算法如下所示:

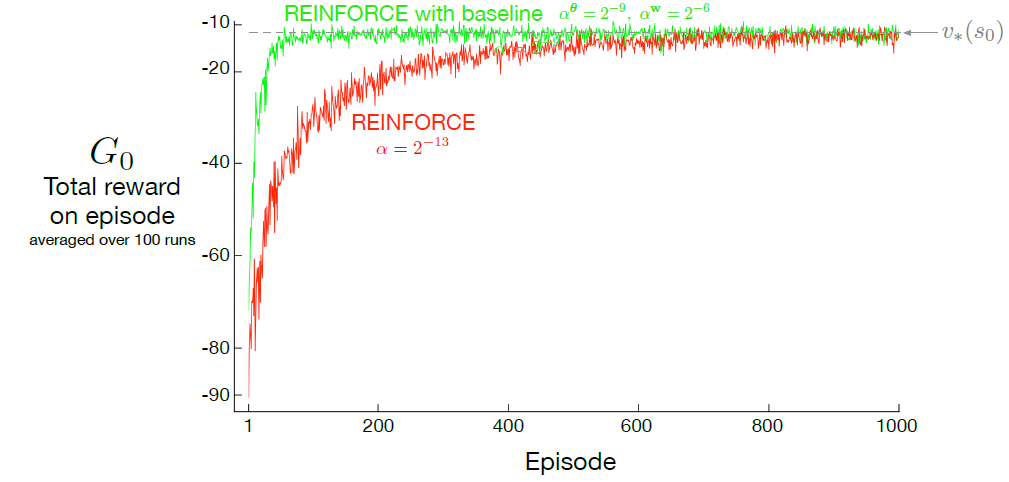
伪代码中有两个重要系数αw\alpha^wαw和αθ\alpha^\thetaαθ,线性情况下我们有经验法则来设置αw\alpha^wαw:αw=0.1Eμ∥∇v^(st,w)∥2\displaystyle \alpha^w=\frac{0.1}{E_{\mu}\parallel \nabla\hat v(s_t,w)\parallel_2}αw=Eμ∥∇v^(st,w)∥20.1,但是αθ\alpha^\thetaαθ的最佳值取决于折扣累计回报的变化范围和策略参数化。如下图所示基线的添加更快更稳收敛。
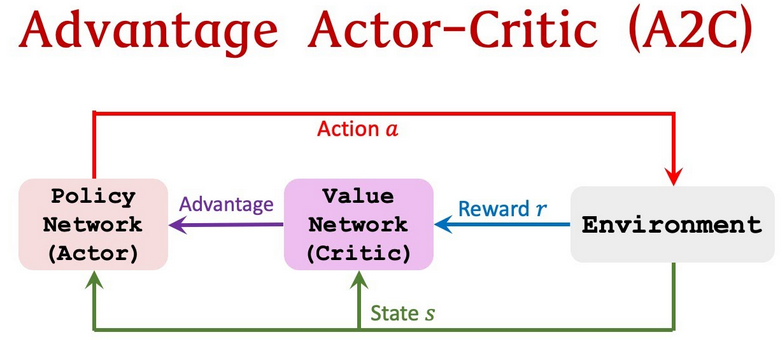
Actor–Critic Methods
对Actor–Critic的理解:
输出策略、负责选择动作的网络称为Actor,负责计算每个动作的分数、预期在未来获得的所有回报的总和的网络称为Critic。Actor通过Critic给出的分数,去学习:如果Critic给的分数高,那么Actor会调整这个动作的输出概率;相反,如果Critic给的分数低,那么就减少这个动作输出的概率。Actor通过Critic给出的分数,去学习:如果Critic给的分数高,那么Actor会调整这个动作的输出概率;相反,如果Critic给的分数低,那么就减少这个动作输出的概率。
基线方法强化了一个策略和一个状态值函数,但不认为它是一个演员-评论家方法,因为它的状态值函数只被用作基线,而不是批评家,不用于引导,不根据后续状态的估计值更新当前状态的估计值。基线强化是无偏的,但与所有蒙特卡罗方法一样存在学习缓慢(产生高方差估计)、不便于在线实施或持续出现的问题。而通过自举,能引入偏差和对函数逼近质量的渐近依赖,使用时间差分的方法减少方差加速学习,且通过n-step可以灵活地调整自举的程度。
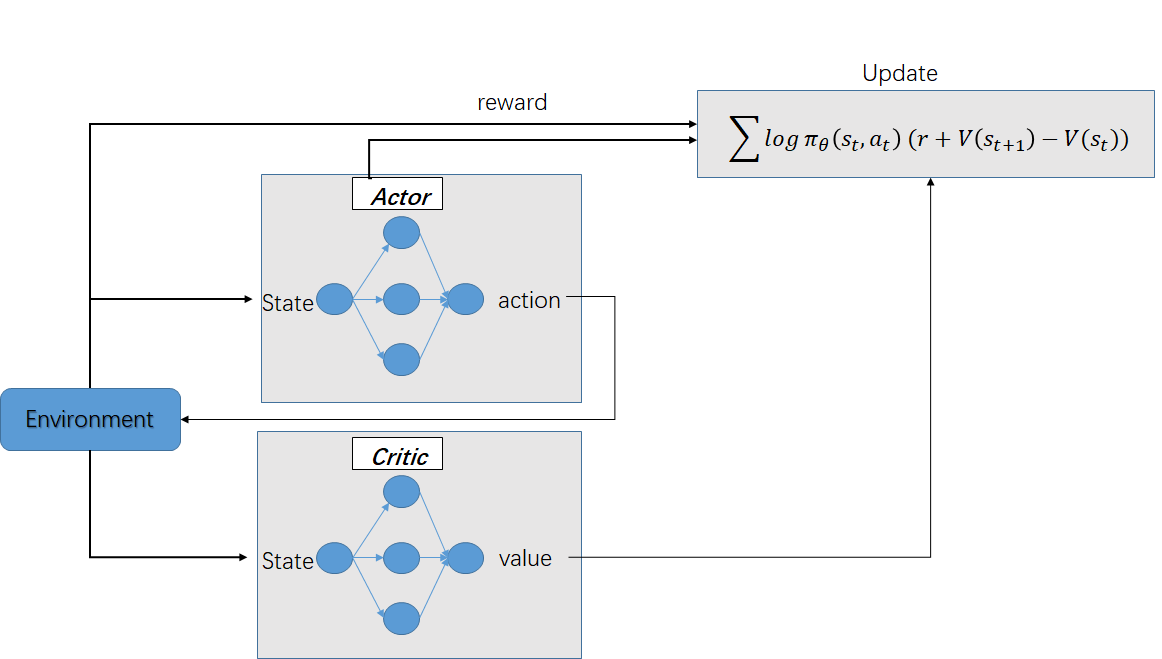
one-step actor–critic methods:
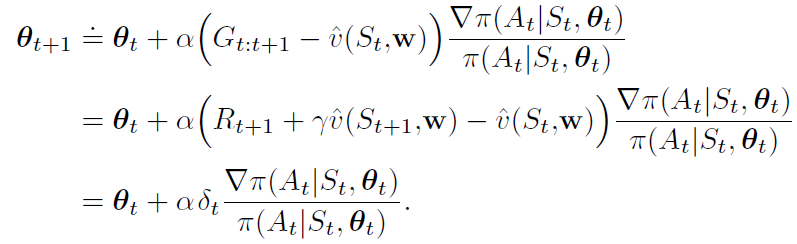

将one-step方法推至前向视角的n-step和λ\lambdaλ-return方法只需将one-step return分别替换为Gt:t+nG_{t:t+n}Gt:t+n或GtλG_{t}^\lambdaGtλ即可;推至后向视角的λ\lambdaλ-return方法需要分别为actor and critic使用资格迹。

Policy Gradient for Continuing Problems
对于非回合制的连续问题我们需要根据每个时间步的平均回报率来衡量智能体表现
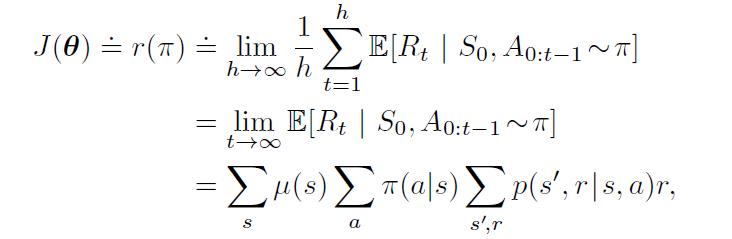
μ\muμ是π\piπ下的稳定状态分布(t→∞t\to∞t→∞理解)。后向视角actor–critic算法在连续状态情况下的完整的伪代码如下:

Policy Parameterization for Continuous Actions
基于策略的方法是处理大动作空间甚至无穷个动作的连续空间的实用方法。我们不计算每个动作的学习概率,而学习概率分布的统计信息。为了产生策略参数化,策略可以定义为实值标量作用上的正态概率密度,由依赖于状态的参数函数近似器给出平均值和标准偏差。
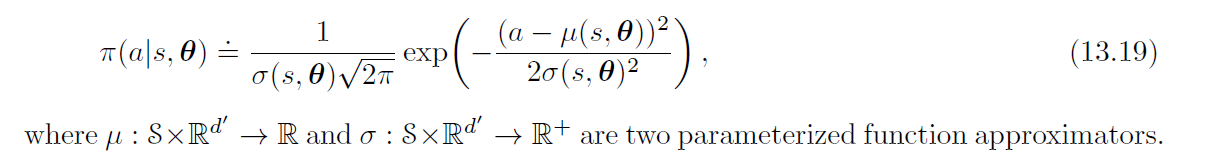
将策略的参数向量人为分为两部分,一部分用于近似平均值,一部分用于近似标准偏差。平均值可以近似为线性函数,而标准偏差必须始终为正,最好近似为线性函数的指数。
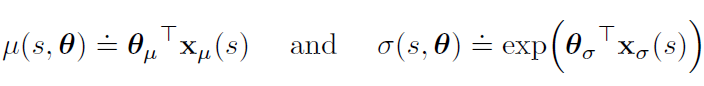
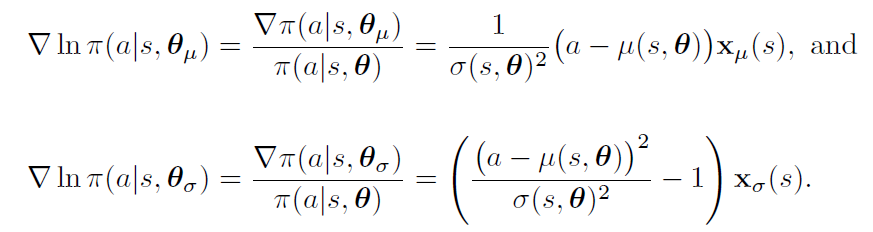
Summary
action-value methods:学习动作值函数,使用一些固定策略模式选择动作
parameterized policy:参数化策略的方法,直接学策略选择动作。特别的,policy-gradient methods在每个时间步上按照相对于策略参数的性能梯度估计的方向更新策略参数
基于策略的方法有很多优点,而对于基于值函数的方法都不可能
-
可以学习到采取行动的具体概率:可以经过适当程度的探索,渐进地接近确定性策略。
-
它们可以自然地处理连续动作空间。
-
某些问题,策略比值函数更易于参数化表示,因此更适合参数化策略方法。
-
参数化策略更容易引入先验知识
REINFORCE方法直接遵循策略梯度定理,添加一个状态值函数作为基线,可以在不引入偏差的情况下减少方差。引入自举TD方法用以改良蒙特卡罗REINFORCE,虽然使用状态值函数进行自举会引入偏差,但能显著降低方差因此往往收敛更稳定快速。状态值函数为对策略的操作选择进行批判性赋值,因此前者称为批评家,后者称为参与者,这些总体方法称为参与者-批评家方法。
Actor-Critic系列总结
AC(Actor-Critic)框架
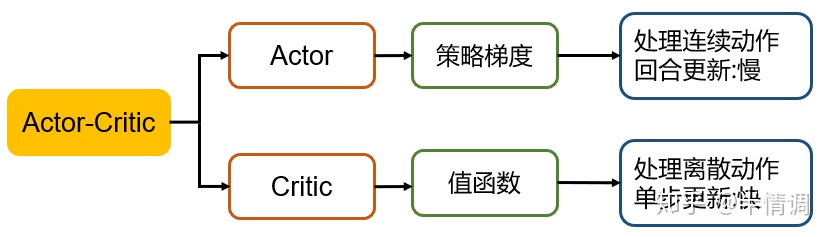

【1–3】直接应用轨迹的回报累积回报,由此计算出来的策略梯度不存在偏差,但是由于需要累积多步的回报,因此方差会很大。
【4—6】利用动作值函数,优势函数和TD偏差代替累积回报,其优点是方差小,但是这三种方法中都用到了逼近方法,因此计算出来的策略梯度都存在偏差。这三种方法以牺牲偏差来换取小的方差。当ψt\psi_tψt取4—6时,为经典的AC方法。其中优势函数如下图:
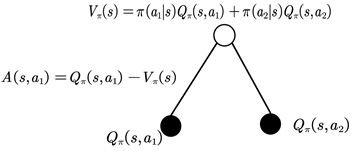

A2C(Advantage Actor Critic)
优势函数AC算法,使用优势函数Aπ(s,a)=Qπ(s,a)−Vπ(s)A_\pi(s,a)=Q_\pi(s,a)-V_\pi(s)Aπ(s,a)=Qπ(s,a)−Vπ(s)代替Critic网络中的原始回报,可以作为衡量选取动作值和所有动作平均值好坏的指标
理解ψt\psi_tψt取优势函数时计算得到的策略梯度方差更小,收敛速度更快:
- 值函数可看成是策略梯度算法中的最优基线函数,基线函数的引入可以减小策略梯度的方差
- 优势函数是动作值函数相对于值函数的优势,若动作值函数比值函数大,那么优势函数为正,其幅值为正,则参数沿着使得该轨迹概率增大的方向更新;若动作值函数比值函数小,那么优势函数为负,策略梯度的幅值为负,则参数沿着使得该轨迹减小的方向更新。
GAE(generalized advantage estimator)
优势函数可进一步写成A^t=−V(st)+rt−V(st+1)\hat A_t=-V(s_t)+r_t-V(s_{t+1})A^t=−V(st)+rt−V(st+1),V都是网络的估计值使得优势函数存在偏差。因此引入GAE方法,改进对优势函数的估计,对优势函数进行多步估计,并将这些多步估计利用衰减因子进行组合,将偏差控制到一定的范围内。
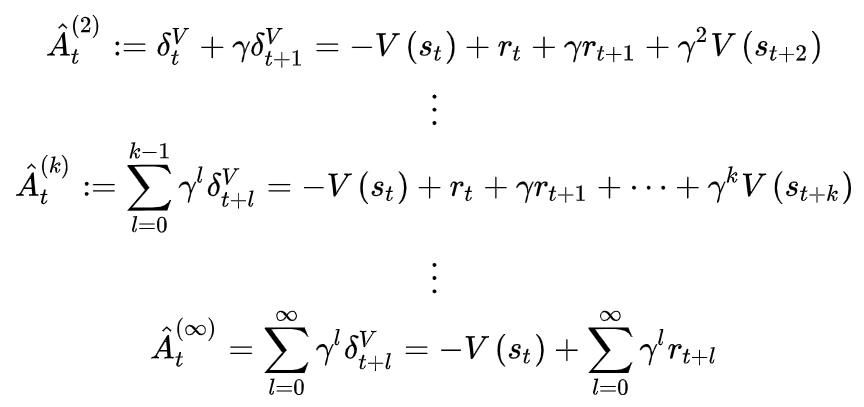
优势函数的k步估计如上,k越大,产生偏差的项γkV(st+k)\gamma^kV(s_{t+k})γkV(st+k)越小,优势函数的估计偏差越小,但相应的方差也会变大。因此提出广义优势函数估计,利用指数加权平均从1步到无穷步的优势函数估计。
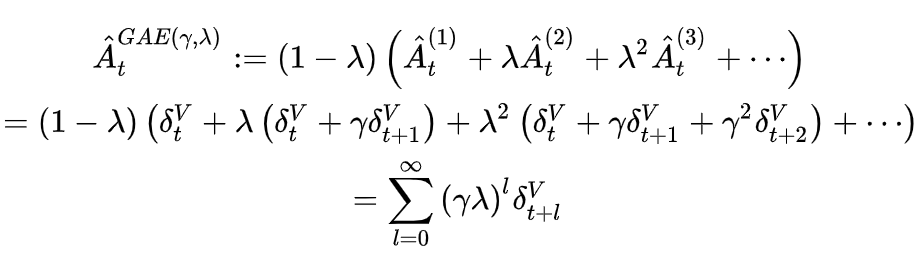
定义转换回报函数
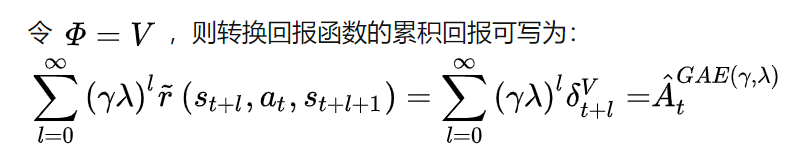
广义优势函数可以看成是回报为转换回报,折扣因子为γλ\gamma\lambdaγλ的折扣累积回报。因此得出结论广义优势函数估计很好平衡了偏差和方差。
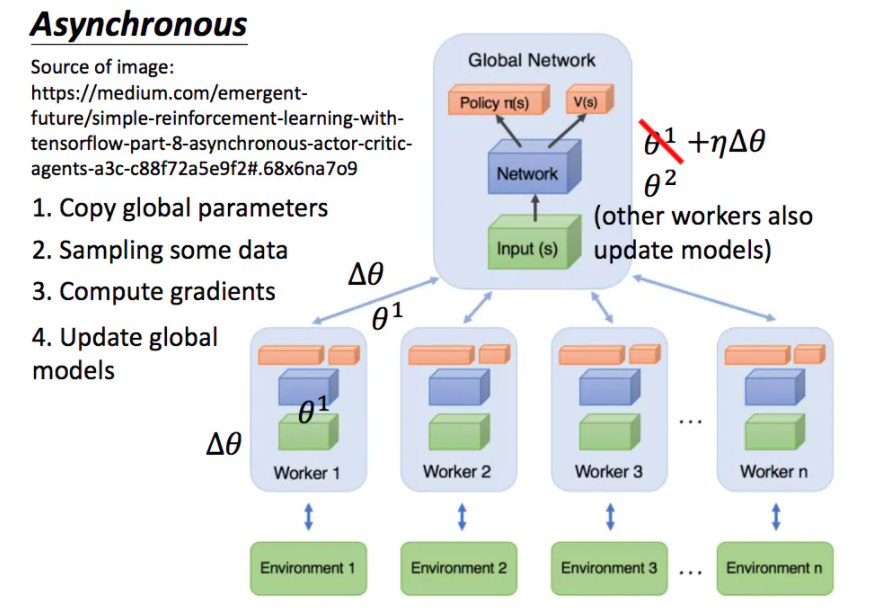
A3C(Asynchronous advantage actor-critic)
异步优势动作评价算法,打破数据的相关性追求数据独立同分布不仅可以通过经验回放还可以异步产生数据。A3C的基本框架还是AC框架,只是它不在利用单个线程,而是利用多个线程。每个线程开始共享全局的参数,并行计算策略梯度,每计算出梯度立即传回中心网络更新参数。A3C的并行机制与谷歌的DPPO是一致的。
Pathwise Derivative Policy Gradient
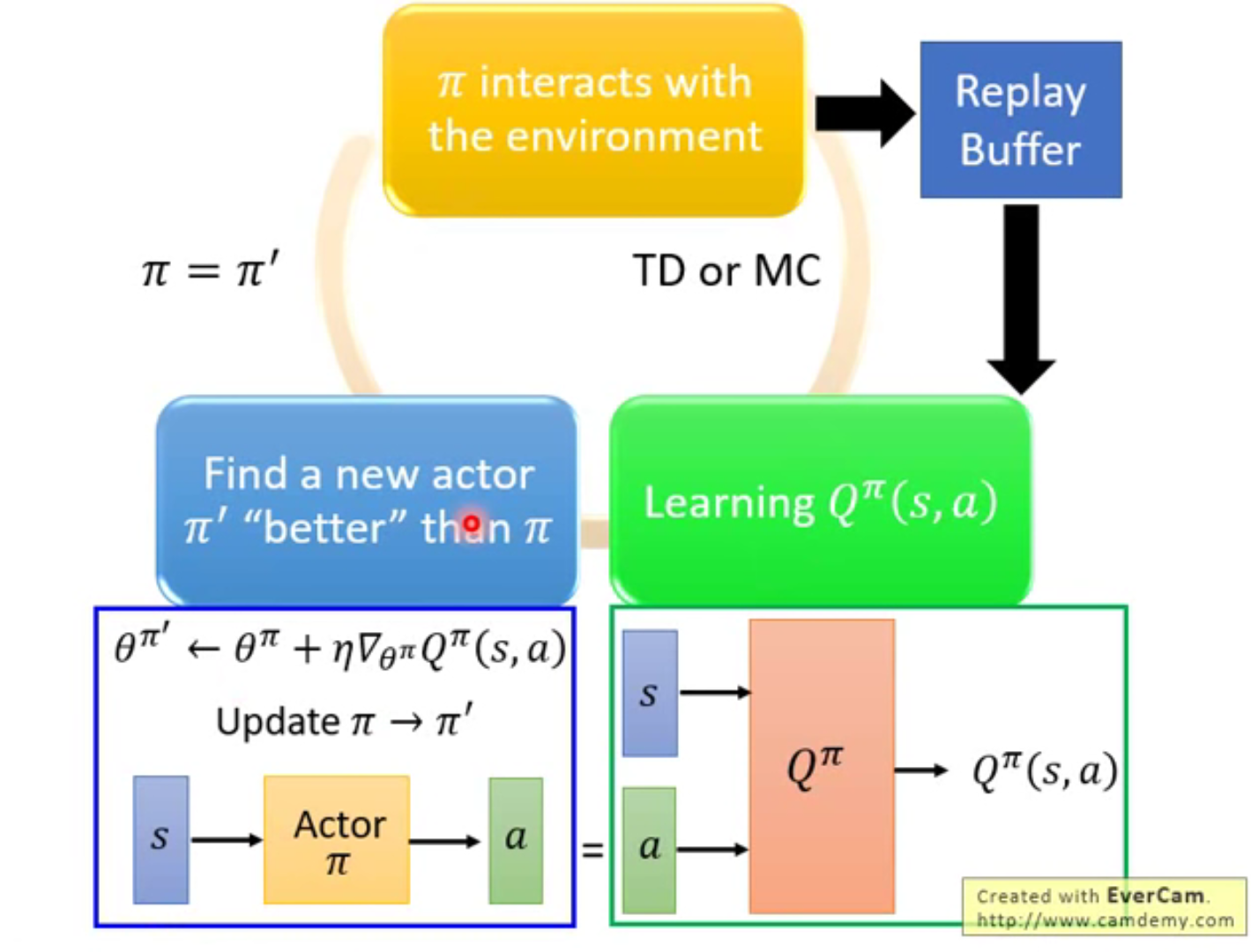
从DQN到pathwise derivative policy gradient
 ----
----





















 2343
2343

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








