120. 三角形最小路径和

给定一个三角形 triangle ，找出自顶向下的最小路径和。

每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说，如果正位于当前行的下标 i ，那么下一步可以移动到下一行的下标 i 或 i + 1 。

这题的思路其实还是蛮简单的，就是对于代码的实际运用需要一些想法。

思路：

从底往上进行递推，先从下面选出两个相邻数中的小的数字，再去向上一行加，这样能保证下面的路径是上面的元素对应的最短的路径。如图，在4,1,8,3中，为了给第三行的6选出最优的路径，就要从4,1选出最小的值1；同理，为了给第三行的5选出最优的路径，就要从1，8选出最小的值1；同理7选3。

于是暂时局部的最小和就是7,6,10。

然后继续循环以上操作，给第二行的元素选择最短路径。3选min（7,6）,4选min（6，10），于是更新最后的数据：9(3+6)，10（4+6）。

然后就是第一行，只剩一个选项，2，选择min（9,10），得到最终的最小路径和11。

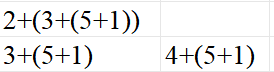
代码实现

public static int minimumTotal(List<List<Integer>> triangle) {
        int n = triangle.size();
        int[] nimPath = new int[n+1];
        for (int i= n-1; i >= 0; i--)
            for (int j = 0; j < triangle.get(i).size(); j++) {
                nimPath[j] = Math.min(nimPath[j], nimPath[j + 1]) + triangle.get(i).get(j);
            }
        return nimPath[0];
    }

总结：在思路上这道题很清晰，就是在代码实现上，需要灵活选择合适的办法实现该思路。通过定义一个长度为n+1的数组，实现局部最小路径的存储，然后在一行一行的往上重复，最后就能得到全局的最小路径和。