聚碳酸酯尿烷粘弹性性能评估

聚碳酸酯尿烷用于医疗器械的粘弹性力学性能评估

目录列表可在ScienceDirect生物医学材料机械行为杂志期刊主页：www.elsevier.com/locate/jmbbm

关键词 ：聚碳酸酯尿烷 医疗器械 粘弹性 伯格斯 特伦‐博伊斯 植入材料

摘要

基础研究工作介绍了一项关于用于制造各种医疗器械的聚碳酸酯尿烷（PCU）力学性能的研究。该研究包括讨论合适的材料模型，通过基本实验确定相关参数，以及对所施加的实验进行数值模拟，以校准和验证数学模型。特别地，用于模拟PCU响应的首选模型是非线性粘弹性伯格斯特伦‐博伊斯材料模型，该模型应用于有限元（FE）软件Abaqus®中。为了进行参数识别，在实验室生理条件下进行了单轴拉伸和无约束压缩试验。试样几何形状以及施加的载荷在Abaqus®中进行了仿真，以确保建模方法的适用性。获得的参数显示出数值与实验结果之间具有非常好的一致性。

引言

聚碳酸酯尿烷（PCU）属于用于医疗器械的弹性体类别，其特点是具有非线性和应变率相关的力学行为。由于其生物相容性和机械性能，已被应用于导管、血管移植物、人工心脏瓣膜和起搏器导线（圣约翰，2014；汗等人，2005a，2005b）。此外，由于与交联超高分子量聚乙烯（UHMWPE）相比具有更好的耐磨性，聚碳酸酯尿烷（PCU）被用于硬对软轴承，以模拟髋关节置换术中的髋臼、膝关节置换术中的半月板（柯尔茨，2009；圣约翰和古普塔，2012；谢梅什等人，2014），或用于人工椎间盘（本策尔等人，2011；范登布鲁克等人，2012）。此外，聚碳酸酯尿烷（PCU）组件还被整合到多种脊柱后路动态稳定装置（PDSD）中，以提高装置的柔韧性和黏性阻尼，例如ZimmerSpine公司，美国的Dynesys®、Spine Vision股份有限公司，比利时的Flex+2®、Orthofix, Inc.的TDX®或Globus Medical公司的 Transition®等。

除了临床研究外，脊柱植入物的性能通常通过认证机构描述的标准化测试来评估，这些测试采用体外测试或数值模拟方法。文献中可以找到多篇关于带有PCU组件的植入物的数值研究。Gabarree等人（2014）和Elsner等人（2010）Gabarree et al. (2014) 和Elsner等人（2010）采用超弹性Mooney‐Rivlin材料模型进行有限元研究，以模拟由 Bionate® 80A PCU制成的人工半月板。使用有限元方法研究最为广泛的后路动态稳定装置（PDSDs）是Dynesys（Lin等人，2013；Tsai等人，2016；Shin等人，2007；Jahng等人，2013；Kim等人，2009；Kiapour等人，2012；Shih等人，2012； Zhang等人，2009；Zhang和Teo，2008；Liu等人，2010；Park等人， 2015），以及Flex+（Zhang等人，2009；Galbusera等人，2011）。

然而，许多已发表的相关数值研究存在一个共同的缺点，即采用了纯弹性材料模型，而忽略了聚碳酸酯尿烷（PCU）特有的阻尼特性。仅有少数研究，如Lawless等人（2016）和Benzel等人（2011），通过确定弹性与阻尼参数，研究了含PCU阻尼器的脊柱植入物的吸能特性。

关于实验研究，值得一提的是，标准化PCU试样的制造具有挑战性且成本较高，因为需要制作注塑模具。因此，文献中采用标准化测试方法研究PCU力学性能的研究较少。例如，Nic An Ghaill和Little（2008）对Bionate® 80A和Bio‐nate® 75D试样在37.5 ° °C下进行了体积压缩试验、单轴拉伸试验和等双轴拉伸试验，以测量其体积模量、杨氏模量和泊松比，用于垫层式轴承的应用。该研究中观察到了应变率依赖性，并确定Bionate®80A的泊松比约为0.49。Bionate®80A材料性能对浸泡时间和温度的显著依赖性由Shemesh等人（2014）和Geary等人（2008）揭示，其中发现Bionate®材料在浸泡两星期至一个月后达到吸水平衡。

本研究的目的是通过标准化测试评估Bionate® II PCU材料的粘弹性力学性能并校准Bionate®II 80A和90A的粘弹性材料模型。具体而言，利用实验结果对一种具有耶奥超弹性和伯格斯特伦‐博伊斯粘弹性的非线性粘弹性框架模型（见第3.2节）进行了参数识别研究，参见Yeoh(1990)、 Bergström（1998）、Bergström和Boyce (2000)以及Dal和 Kaliske (2009)等。所确定的材料参数可用于通过有限元方法预测植入物在生理载荷条件下的变形、应力和蠕变。为此，在生理条件下对 Bionate® II 80A和90A聚碳酸酯尿烷（PCU）（DSM生物医学，加利福尼亚州伯克利）进行了单轴拉伸和无约束压缩试验。

综上所述，第2节 介绍了实验方法，接着在第3.1节–3.2节 中阐述了所用模型的理论基础，以及第3.3节中的参数研究方法。实验结果在第 4.1节–4.2节 中展示，标定后的材料模型见第5节。第6节 对本研究进行了总结概述。

2. 实验材料与方法

2.1. 实验材料

在本研究的测试中，采用注塑成型和水射流切割法制备了两种不同几何形状的Bionate® II 80A和90A材料的试样。压缩试验使用直径为29 mm、高度为12.5 mm的圆柱形试样，其制造依据ASTM-D (6147)-97(2014)中7.1.2型试样的规定。拉伸试验则采用哑铃形试样 （图1a），按照DIN EN ISO 527-2(2012)中1BA型试样的规定制备，测试长度为25 mm，总长度为80 mm，宽度和厚度均为5 mm。

2.2. 测试方法

一个生物反应器（图1b），安装在由MTS，加拿大生产的单轴液压测试机上，用于控制温度并防止通过在加热蒸汽环境中测试，使浸泡试样干燥。蒸汽使用常规的超声波雾化器持续供应，并连接至生物反应器。生物反应器采用带有蒸汽提取系统的聚乙烯套管进行密封。为了在测试过程中调节温度，安装了温度控制单元。该单元控制两条加热电缆，分别位于超声波雾化器与生物反应器之间的管道以及试样周围，如图1b所示。此外，通过放置在试样旁边的第三个温度传感器记录温度。测试期间，利用单轴载荷传感器（ HBM GmbH，德国，采样频率100赫兹）测量反作用力和机器位移，并采用光学跟踪系统（Nexonar®，soft2tec GmbH，德国），安装在夹具处以10赫兹频率跟踪整体位移。在初步试验中，尽量减小压缩试样的摩擦和鼓胀，同时防止试样在压缩压板之间滑动。

两种测试材料的测试协议（即加载和边界条件）相同，采用具有恒定位移速率的位移控制方法。根据Qi和Boyce（2005）以及 Bergström（1998）提出的评估弹性体粘弹性行为的方法，进行了拉伸和压缩加载的逐步松弛试验。此外，所有试样在37°C的蒸馏水中持续浸泡至少30天，并经过50个循环、30%应变的预处理。进一步地，试样在不同日期进行预处理和测试，以确保完全松弛的初始状态。每种材料的压缩试验在3个试样上进行，位移速率为0.5mm/s，分别达到5%应变、10%应变和20%应变，并保持时间为60分钟、120分钟和180分钟。对于单轴拉伸试验，每种材料的3个试样以位移速率0.5mm/s加载至60%应变，在5%应变时保持60分钟，在30%应变时保持120分钟，在60%应变时保持180分钟。

由于生物反应器的测量体积处于封闭状态以维持温度和湿度方面的生理条件，无法直接观察试样，因此无法通过该方法评估哑铃形试样中心的局部应变一种光学测量方法。因此，采用了基于夹持式光学跟踪系统的全局应变值。然而，由于拉伸试样的宽度不同，需要对外推局部应变。为此，引入了一个恒定的比例因子，进一步称为应变修正系数。通过在夹具处记录的全局应变和在试样上记录的局部应变，确定了应变修正系数，以获得将全局应变映射到局部应变的函数。具体而言，对四个浸泡后的拉伸试样（两个Bionate® II 80A，两个90A）进行了测试，在未封闭测量体积的情况下使用了额外的光学引伸计（德国Zwick有限公司）。光学引伸计以25毫米的标距长度记录拉伸试样上的局部应变，同时光学跟踪系统记录夹具的位移。

通过使用Matlab®软件（版本9.2.0.538062，美国马萨诸塞州纳蒂克MathWorks公司）计算平均实验曲线的归一化均方根误差（ NRMSE），来检验实验的可重复性。NRMSE是衡量拟合优度的一个指标（fit（Moriasi等人，2007年），可通过两个数据集yref和y进行评估

$$
\text{NRMSE} = \frac{| y_{\text{ref}} - y |}{| y_{\text{ref}} - \text{mean}(y_{\text{ref}}) |}
$$

NRMSE 为 1 表示完全拟合，而 NRMSE 为负无穷（− ∞）表示最差的拟合情况。

3. 材料模型与仿真的方法

文献中可以找到少量描述弹性体行为的材料模型。在此背景下，广义Maxwell模型已被证明是可靠的，因此常用于聚氨酯或其他填充型弹性体的建模（Qi和Boyce，2005年；Bergström，1998年）。因此，本研究选用的模型是广义Maxwell构型下的Bergström‐Boyce模型，该模型能够准确反映PCU材料的非线性、大变形和率相关行为。

3.1. 流变学建模与运动学

广义Maxwell模型可以表示为一个带有纯超弹性弹簧的平衡（EQ）分支，该分支与N个非平衡（NEQ）Maxwell分支并联组成，每个非平衡分支包含粘性阻尼器和弹性弹簧，如图2所示。下文将介绍所考虑模型的运动学方程，而详细的方程和讨论可参见Markert(2005)、Dal和 Kaliske (2009) 以及霍尔扎普费尔（2000）等文献。

在 图2中，N个弹性弹簧的变形情况如下麦克斯韦元件由弹性变形梯度表示F()e n，而每个−N 1阻尼器的变形则用非弹性变形梯度F()i n表示，其中 ∈n N[1, 2,.. ]。因此，模型的总变形梯度F可对每一分支进行乘积分解，分为弹性Fe和非弹性Fi部分，如下所示

$$
F = F^e F^i
$$

使用公式 (2)，相应地可推导出柯西‐格林变形张量C为

$$
C = F^T F
$$

具有 $\dot{F}$ 作为F的物质时间导数，速度梯度L可分解为弹性部分和非弹性部分，可根据公式(2)推导如下：

$$
L = \dot{F}F^{-1} = (\dot{F}^e F^i + F^e \dot{F}^i)(F^i)^{-1}(F^e)^{-1} = \dot{F}^e(F^e)^{-1} + F^e \dot{F}^i(F^i)^{-1}(F^e)^{-1}
$$

此处，非弹性速度梯度 $\tilde{L}_i$ 是中间构型中的一个量，表示为 $\tilde{L}_i = \dot{F}^i (F^i)^{-1}$，其中$\tilde{L}_i F^e (F^i)^{-1}$ 是非弹性速度梯度，与当前构型相关。非弹性速度梯度张量可加性分解为非弹性变形速率张量 $\tilde{D}_i$ 和非弹性自旋张量$\tilde{W}_i$，即

$$
\tilde{L}_i = \tilde{D}_i + \tilde{W}_i
$$

此外，非弹性速度梯度被视为完全对称，因此将反对称的非弹性旋率张量$\tilde{W}_i$设为零（Bergström 和 Boyce，2000）。

类橡胶材料的应变能函数通常用雅可比行列式 $J = \det F$ 表示体积变形，以及修正的（等容）右柯西‐格林变形张量C的第一和第二不变量（$I_C$ 和 $II_C$）来表示：

$$
W = W_{\text{vol}}(J) + W(\bar{I}_C, \bar{II}_C)
$$

$$
\bar{I}_C = J^{-2/3} \text{tr}(C), \quad \bar{II}_C = J^{-4/3} \text{tr}(C^2)
$$

$$
\bar{II}_C = \frac{1}{2}((\text{tr} C)^2 - \text{tr}(C^2))
$$

柯西应力张量 τ可加性地分解为一个静水（体积）部分，其中p为静水压力，以及一个偏应力（等容）部分

$$
\tau = \tau_{\text{hyd}} + \tau_{\text{dev}}, \quad \tau_{\text{hyd}} = p I, \quad \tau_{\text{dev}} = \tau - \frac{1}{3}\text{tr}(\tau) I
$$

偏应力Kirchhoff 应力张量的等效应力可根据定义进行定义，该定义来源于Abaqus(2014)，其使用了Kirchhoff 应力的第二偏应力不变量，即

$$
\tau_{\text{eq}} = \sqrt{\frac{3}{2} \text{tr}(\tau_{\text{dev}}^2)} = \sqrt{\frac{3}{2} \tau_{\text{dev}} : \tau_{\text{dev}}}
$$

$$
\tau_{\text{eq}} = \sqrt{\frac{3}{2} \tau_{\text{dev}} : \tau_{\text{dev}}}, \quad \text{with } \tau_{\text{dev}} : \tau_{\text{dev}} = \tau_{\text{dev}} \cdot \tau_{\text{dev}}
$$

其中tr(·)为迹算子。

3.2. Bergström‐Boyce模型

在本研究中，使用Abaqus®仿真软件（Hurtado 等，2013； Abaqus，2014，分析用户指南22.8.2）采用了一个包含一个平衡支路和三个非平衡支路的并联流变框架模型(PR F)。该PRF模型在两个方面不同于广义Maxwell模型，以减少材料参数的数量。首先，引入了各个分支的权重参数。其次，所有弹性弹簧均采用相同的超弹性本构关系，因此它们具有相同的材料参数和应变能表达式。总应力响应等于所有N个弹性弹簧应力的总和。因此，并联流变框架模型的总应变能（W tot）可通过所有弹性组分的加权求和计算得到

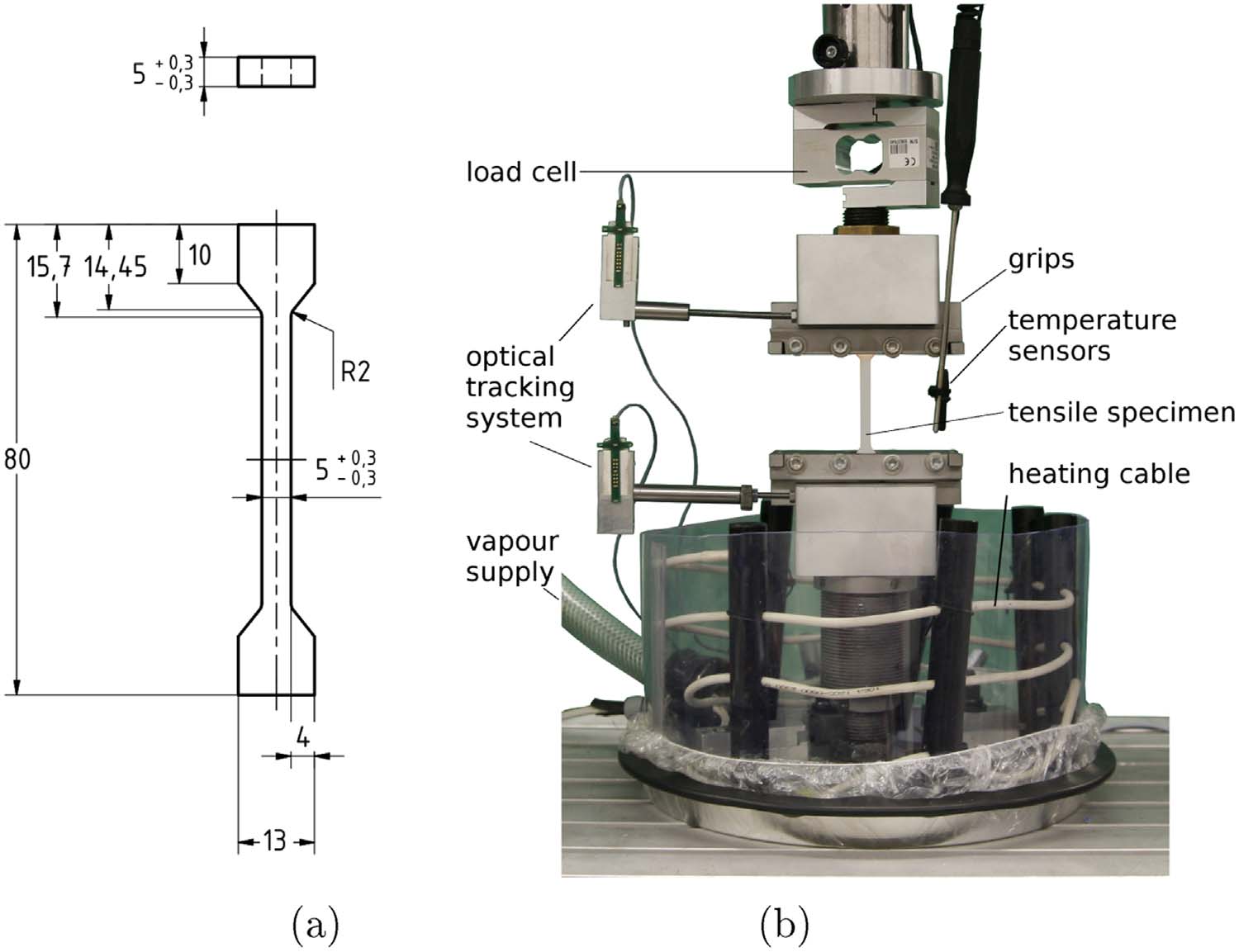
图2。广义 Maxwell模型，包含一个弹性分支，该分支由一个弹簧单元（平衡 EQ）和 N 1个粘弹性分支组成，这些分支由弹簧单元和阻尼单元（非平衡 NEQ）构成。

A. 贝克曼等人 生物医学材料机械行为杂志 82 (2018) 1–8
3

$$
W_{\text{tot}} = \sum_{n=1}^{N} S_n W_e(C_e^n)
$$

$$
\tau_{\text{tot}} = \sum_{n=1}^{N} S_n \tau_n, \quad \tau_n = 2 \frac{\partial W_e(C_e^n)}{\partial C_e^n} F_e^n (F_e^n)^T
$$

其中 $S_n$ 为权重参数，需满足以下条件

$$
\sum_{n=1}^{N} S_n = 1
$$

$\tau_n$ 是应力，而 $W_e(C_e^n)$ 是第n个分支的应变能。
需要指出的是，本研究未考虑塑性和穆林斯效应。

对于近似不可压缩且高度非线性的炭黑填充弹性体的建模，从超弹性材料中选择了简化多项式模型，例如耶奥模型或阿鲁达‐博伊斯模型，参见霍尔扎普费尔（2000）。本研究采用耶奥模型，该模型是具有三个等容项和三个体积项的简化多项式模型的一种特定形式，用于模拟

和 Bionate® II 90A ( 右 ) 在5%、10%和20%全局应变水平下的逐步松弛压缩试验)

A. 贝克曼等人 生物医学材料机械行为杂志 82 (2018) 1–8
4

PCU材料的弹性响应。耶奥模型的应变能函数表示为第一偏应变不变量和体积应变不变量的函数，而忽略了第二偏应变不变量（first deviatoric strain in-variant and the volumetric strain invariant, whereas thesecond de-viatoric strain invariant is neglected(Yeoh， 1990）。具体而言，耶奥模型的应变能函数为

$$
W = C_{10}(I_C - 3) + C_{20}(I_C - 3)^2 + C_{30}(I_C - 3)^3 + \frac{1}{D_1}(J - 1)^2 + \frac{1}{D_2}(J - 1)^4 + \frac{1}{D_3}(J - 1)^6
$$

有关材料参数的讨论见 Abaqus, Analysis Theory Maual 4.6.1)(2014)。
其中，小应变范围内的初始剪切模量 $\mu_0$ 由正参数 $C_{10} = \frac{1}{2} \mu_0$ 表示。参数 $C_{20}$ 大约比 $C_{10}$ 小十倍且为负值（即 $C_{20} \approx -\frac{1}{10} C_{10}$），在中等应变下起到降低剪切模量的作用。正参数 $C_{30}$ 大约比 $C_{10}$ 小一百倍（ $C_{30} \approx \frac{1}{100} C_{10}$），有助于在较大应变下增加剪切模量。通过该本构模型，可获得呈S形的应力‐应变曲线，这在碳纤维填充弹性体中具有典型性。

材料的体积变形由压缩性参数 $D_1, D_2$ 和 $D_3$ 以及小应变下的初始体积模量 $K_0 = \frac{2}{D_1}$ 控制。对于完全不可压缩材料，$D_1, D_2$ 和 $D_3$ 等于零，且雅可比行列式 $J = 1$。

粘弹性本构定律能够模拟应力松弛和蠕变，这是生物组织或热塑性橡胶类材料等的典型特征。公式(14)中引入的应变能函数描述了粘弹性材料的弹性贡献和平 衡状态。非弹性的、耗散的黏性部分由于材料响应的率相关性而引起非平衡效应。根据Bergström和Boyce (2000)Bergström和Boyce (2000) 在Abaqus分析用户指南22.8.2 (2014)中的实现方法，可以利用非弹性变形速率张量 $D_i$ 建立一个演化方程，该方程依赖于偏应力Kirchhoff 应力 $\tau_{\text{dev}}$、有效偏应力Kirchhoff 应力 $\tau_{\text{dev}}$ 以及等效蠕变速率 $\dot{\gamma}_i$，表达式为

$$
\tilde{D} i = \frac{2}{3} \dot{\gamma}_i \frac{F_e^i \tau {\text{dev}} (F_e^i)^T}{|\tau_{\text{dev}}|}
$$

$$
\dot{\gamma} i = A \left(1 - \frac{\text{tr}(\tau {\text{dev}})}{3} + E\right)^C (\tau_{\text{eq}})^m
$$

在公式(16)中，$A$、$E$、$C$ 和 $m$ 是模型参数，其中每个粘弹性分支由一个蠕变参数 $A$、一个等效应力指数 $m$、一个蠕变应变指数 $C$ 以及一个附加常数 $E$ 表示。根据Bergström和Boyce (2000)，项 $-\frac{\text{tr}(\tau_{\text{dev}})}{3} + E)^C$ 反映了黏度的拉伸依赖性。特别是指数 $C$ 和 $m$ 控制着松弛和非弹性流动的动力学（Dal和Kaliske，2009）。材料参数 $E$ 调节未变形状态附近的蠕变应变率（Abaqus，2014，分析用户指南22.8.1）。通过定义 $C = 0$ 和 $m = 1$，可得到Reese和Govindjee（1998）提出的广义有限粘弹性模型。等效变形速率的推导在Bergström（1998）、Bergström和 Boyce (2000) 以及Dal和Kaliske (2009) 中有详细描述。

3.3. 参数研究与仿真的方法

材料参数的标定通过优化软件（MCalibration®，Veryst Engineering LLC，美国马萨诸塞州）半自动完成，该软件采用了 NEWUOA（新的无约束优化算法）优化算法，详细描述见Powell (2008)。实验与模拟的应力‐应变曲线的总决定系数 $R^2$ 值进行了优化，优化过程使用了一个单元以及MCalibration®内置的有限元求解器。经过使用一个元件进行校准后，所进行的实验

表1 Bionate® II 80A 的 PRF模型参数，包含耶奥超弹性（EQ）和贝尔格斯特伦‐博伊斯粘弹性（NEQ），具有三个并行分支。

EQ	C10	C20	C30	D1	D2	D3
	[兆帕]	[兆帕]	[兆帕]	[ − 兆帕¹ ]	[ − 兆帕¹ ]	[ − 兆帕¹ ]
网络 1	7.62589	−3.2927	1.31708	0.001	0	0

NEQ	S	A	m	C	E
	[-]	[ −秒¹ ]	[-]	[-]	[-]
网络 2	0.111671	1.00416e−4	8.48285	−0.659688	0.001
网络 3	0.660553	4.63605e−3	1.58	−0.7	0.001

表 2 PRF的参数采用耶奥超弹性（EQ）和伯格斯特伦‐博伊斯粘弹性（NEQ）的模型，包含三个并行分支，适用于Bionate® II 90A。

EQ	C10	C20	C30	D1	D2	D3
	[兆帕]	[兆帕]	[兆帕]	[ − 兆帕¹ ]	[ − 兆帕¹ ]	[ − 兆帕¹ ]
网络 1	13.0914	−4.97324	1.74405	0.001	0	0

NEQ	S	A	m	C	E
	[ -]	[ − 秒¹ ]	[ -]	[ -]	[ -]
网络 2	0.177468	3.97624e−7	11.3587	−0.461823	0.001
网络 3	0.621849	8.45938e−4	1.58106	−0.972286	0.001

A. 贝克曼等人 生物医学材料机械行为杂志 82 (2018) 1–8
5

使用隐式 Abaqus® CAE 软件（6.14，达索系统，法国）对拉伸和压缩试验的平均试样几何形状进行了模拟。通过 Abaqus® CAE 预处理器，采用具有完全积分的二次杂交六面体单元（C3D20H）对试样几何形状进行网格划分。拉伸试样的夹紧端被视为刚性，而无侧限压缩试验则视为无摩擦。位移控制的加载按照与实验相同的协议定义（见第2节）。对比了实验和仿真的平均工程应力‐应变曲线。使用MCalibration®软件进行准静态模拟，以预测材料在拉伸和压缩加载方向上以 $10^{-2} \sim 10^{-3} \cdot \text{秒}^{-1}$ 的连续速率下的平衡行为。

4. 结果与讨论

4.1. 局部应变修正系数

如第2节所述，由于实验在封闭的蒸汽填充腔室中进行，无法使用光学测量系统直接记录局部应变。因此，还在开放系统中进行了额外的实验，以获得应变修正系数，从而根据全局测量的应变评估局部应变。计算得到的修正系数是通过开放系统中四次拉伸试验的应变修正曲线的中位数，这些试验在夹具处和试样局部位置使用了两个光学测量系统进行测量（图3）。最终得到的中位数应变修正系数为 1.1181，用于将全局应变映射到局部应变。应用该修正系数后，整体拟合优度（以公式 (1)中的NRMSE准则表示）从0.77提高至0.96，如图3所示。这相当于均方误差从0.0024 mm²改善至 $9.51 \times 10^{-5}$ mm²。在封闭腔室中进行的后续拉伸试验中，只能测量全局应变，因此所有拉伸应变数据均使用了 1.1181的修正系数。

4.2. 拉伸和压缩循环松弛试验

按照Qi和Boyce（2005）和Bergström（1998）中所述的程序来确定与粘弹性相关的参数，对试样进行了拉伸和压缩载荷下的逐步松弛试验。如图4和图5所示，在三个保持时间内，应力向平衡应力松弛。已生成并绘制了一条参考或平均曲线，即“平均值”，该曲线基于测量曲线的算术平均值得出。对于粘弹性材料，平衡应力曲线不依赖于加载历史，而仅取决于当前局部应变。因此，可通过完全松弛状态下的应力值评估应力‐应变平衡曲线，也可通过试样的准静态（非常缓慢）加载获得该曲线。

拉伸或压缩加载下的粘弹性行为通过工程应变与工程应力的关系图表示，如图6和图7 所示。为了评估所进行实验的可重复性，计算了测量曲线相对于平均曲线的归一化均方根误差（NRMSE）。单轴拉伸试验相对于平均曲线的应变和应力测量的平均NRMSE分别为0.99和0.93（图 6）。压缩试验相对于平均曲线的应变和应力测量的平均NRMSE分别为 0.99和0.91（图7）。综上所述，所有单轴试验的平均NRMSE为0.96，表现出良好的可重复性。

5. 模型参数和验证

根据第3.3节所述方法获得的Bionate® II 80A和90A的材料参数分别总结于表1和表2中。

圆柱形压缩试样和哑铃形拉伸试样在不同时间步的变形和冯·米塞斯应力，其材料参数来自表2，如图8所示。表 2 中所示。图8。

基于上述参数，图9 展示了Bionate–® II80A和90A的实验工程应力 ®应变曲线以及基于试样几何形状的相应数值模型。实验结果与数值结果之间的比较显示，Bionate®II 80A的决定系数为 $R^2 = 0.952$，Bionate® II 90A的决定系数为 $R^2 = 0.955$。在中等应变范围内，数值应力‐应变曲线与实验曲线具有非常好的一致性，而在小和大应变范围则存在较大的偏差。特别是可以观察到，两种材料在小应变下的应力松弛均被低估。

为了获得平衡曲线，使用MCalibration®的求解器对一个单元进行了仿真，并以应变率 $10^{-2} \sim 10^{-3} \cdot \text{秒}^{-1}$ 进行连续准静态加载。基于试样几何形状的仿真及所得平衡曲线如图10所示。平衡曲线相对于应变呈现非线性变化趋势，这反映了所考虑的伯格斯特伦‐博伊斯模型为非线性粘弹性。

6. 结论与展望

在这项研究工作中，两种PCU材料（Bionate® II）的

A. 贝克曼等人 生物医学材料机械行为杂志 82 (2018) 1–8
7

邵氏硬度80A和90A的材料用于可植入医疗器械，在单轴拉伸和无侧限压缩试验中进行了测试。实验在生理条件下进行，使用充满37°C蒸汽的封闭式温控室。为了模拟非线性粘弹性材料，采用了在有限元软件包 MCalibration®和Abaqus®中应用的Bergström‐Boyce材料模型。数值与实验结果之间良好的一致性表明了该模型在测试应变范围内用于 PCU材料的有效性。所确定的参数可用于评估含有PCU材料的医疗器械性能，并结合商业有限元工具中的有限元方法进行分析。在未来的研究中，将进行剪切试验，并使用已标定的参数与数值结果进行比较。此外，研究PCU材料在循环加载下的行为也具有重要意义，其中可能涉及疲劳响应和循环硬化现象。这将有助于预测植入物可能发生的塑性变形。