算法与数据结构-第四章：栈与队列

1.栈与队列:

栈是限定仅在表尾进行插入和删除操作的线性表。
队到是只允许在一端进行插入操作、 而在另一端进行删除操作的线性表.
 

书中的例子讲的挺好的,直接复制过来:

在软件应用中 ，栈这种后进先出数据结构的应用是非常普遍的。

比如你用浏览器上网时 ， 不管什么浏览器都有一个"后退"键，你点击后可以接访问顺序的逆序加载浏览过的网页。比如你本来看着新闻好好的，突然看到一个链接说，有个可以让你年薪 100 万的工作，你毫不犹豫点击它， 跳转进去一看，这都是啥呀，具体内容我也就不说了，骗人骗得一点水平都没有 。

此时你还想回去继续看新闻 ， 就可以点击左上角的后退键。

即使你从一个网页开始 ， 连续点了几十个链接跳转 ， 你点"后退"时 ， 还是可以像历史倒退一样，回到之前浏览过的某个页面,

       很多类似的软件，比如 Word 、 Photoshop 等文档或图像编辑软件中 ， 都有撤销的操作，也是用栈这种方式来实现的，当然不同的软件具体实现代码会有很大差异，不过原理其实都是一样的。
 

栈( stack )是限定仅在表尾进行插入和删除操作的线性表。

 

理解栈的定义需要注意 :

 

首先它是一个线性表 ，也就是说，栈元素具有线性关系，即前驱后继关系。只不过它是一种特殊的线性表而已。定义中说是在线性表的表尾进行插入和删除操作，这里表尾是指栈顶,而不是栈底。
      它的特殊之处就在于限制了这个线性表的插入和删除位置，它始终只在栈顶进行。这就使得:栈底是固定的，最先进栈的只能在栈底。

栈的插入操作，叫作进栈，也称压栈、人栈。 类似子弹入弹夹，如图 4-2-2 所示。

栈的删除操作，叫作出栈，也有的叫作弹栈。如同弹夹中的子弹出夹，如图 4-2-3所示。

 

 

1.1进栈出栈变化形式

最先进栈的元素，是不是就只能是最后出战呢?

答案是不一定，要看什么情况。栈对线性表的插入和删除的位置进行了限制 ，并没有对元素进出的时间进行限制，也就是说，在不是所有元素都进栈的情况下，事先进去的元素也可以出栈，只要保证是栈顶元素出栈就可以。
 

比如:

举例来说，如果我们现在是有 3 个整型数字元素 1 、 2、 3 依次进栈，会有哪些出栈次序呢?

• 第一种: 1 、 2 、 3 进，再 3 、 2 、 1 出。这是最简单的最好理解的一种，出栈次序为 321 .
• 第二种: 1 进， 1 出， 2 进. 2 出， 3 糙， 3 出。也就是进一个就出一个，出栈次序为123。
• 第三种: 1 进， 2 进， 2 出， 1 出， 3 进， 3 出。出栈次序为 213.
• 第四种: 1 进， 1 出， 2 进， 3 进， 3 出， 2 出。出栈次序为 132.
• 第五种 :: 1 进， 2 进， 2 出， 3 进， 3 出， 1 出。 出栈次序为 231 。

有没有可能是 312 这样的次序出栈呢?答案是肯定不会。因为 3 先出栈，就意味着， 3 曾经进栈，既然 3 都进栈了，那也就意味着， 1 和 2 已经进栈了，此时， 2 一定是在 1 的上面，就是更接近栈顶，那么出栈只可能是 321了.

 

1.2栈的抽象数据类型

栈的抽象数据类型定义如下:

同线性表,元素具有相同的类型,相同的元素具有前驱和后继关系.

具有一些与线性表同样性质的操作: 增删改查.

 

由于栈本身就是一个线性表，那么上一章我们讨论了线性表的顺序存储和链式存储，对于栈来说，也是同样适用的 。
 

2.1栈的顺序存储结构

直接复制:

既然栈是线性表的特例，那么栈的顺序存储其实也是线性表顺序存储的简化，我们简称为顺序栈。 线性表是用数组来实现的，想想看，对于栈这种只能一头插入删除的线性表来说，用数组哪一端来作为栈顶和栈底比较好?

对，没错，下标为 0 的一端作为栈底比较好，因为首元素都存在栈底，变化最小，所以让它作栈底。

我们定义一个 top 变量来指示栈顶元素在数组中的位置，这 top 就如同中学物理学过的游标卡尺的游标，如图 4-4-1，它可以来回移动，意味着栈顶的 top 可以变大变小，但无论如何游标不能超出尺的长度。

同理，若存储栈的长度为 StackSize ，则槐顶位置 top 必须小于 如ckSize。 当栈存在一个元素时top 等于 0 ，因此通常把空栈的判定条件定为 top 等于 -1 .

 

来看栈的结构定义:

 

若现在有一个栈， StackSize 是 5 ，则栈普通情况、空栈和栈满的情况示意图如图4-4-2所示

 

2.2进栈操作

2.3出栈操作

删除栈顶元素,并用一个变量返回元素值,并返回ok,否则返回error.

 

 

3.两栈共享空间

       其实栈的顺序存储还是很方便的，因为它只准栈顶进出元素，所以不存在线性表插入和删除时需要移动元素的问题。

       不过它有一个很大的缺陷，就是必须事先确定数组存储空间大小，万一不够用了，就需要编程手段来扩展数组的容量，非常麻烦 。

       对于一个栈，我们也只能尽量考虑周全，设计出合适大小的数组来处理，但对于两个相同类型的栈，我们却可以做到最大限度地利用其事先开辟的存储空间来进行操作。

       打个比方，两个大学室友毕业同时到北京工作，开始时，他们觉得住了这么多年学校的集体宿舍，现在工作了一定要有自己的私密空间。

      于是他们都希望租房时能找到独佳的一居室，可找来找去却发现，最便宜的一居室也要每月 1500 元，地段还不好，实在是承受不起，最终他俩还是合租了一套两居室， 一共 2000 元，各出一半 ，还不错。对于两个一居室，都有独立的卫生间和厨房，是私密了，但大部分空间的利用率却不高。

       而两居室，两个人各有卧室，还共享了客厅、厨房和卫生间，房间的利用率就显著提高，而且租房成本也大大下降了。

       同样的道理，如果我们有两个相同类型的栈，我们为它们各自开辟了数组空间，极有可能是第一个栈已经满了，再进栈就溢出了，而另一个栈还有很多存储空间空闲 。 这又何必呢?我们完全可以用一个数组来存储两个栈，只不过需要点小技巧 。

 

我们的做法如图 4-5-1 ，数组有两个端点，两个栈有两个栈底，让一个栈的栈底为数组的始端，即下标为 0 处 ，另一个栈为栈的末端，即下标为数组长度 n-1处。这样，两个战如果增加元素，就是两端点向中间延伸。

 

 

其实关键思路是:它们是在数组的两端，向中间靠拢。 topl 和 top2 是栈 1 和栈 2的栈顶指针，可以想象，只要它们俩不见面，两个栈就可以一直使用。
从这里也就可以分析出来，栈 1 为空时，就是 topl 等于-1 时;而当 top2 等于n 时，即是栈2 为空时 ，那什么时候栈满呢?

看图辅助理解:

想想极端的情况，若按 2 是空栈，栈 1 的 topl 等于 n-1 时，就是栈 1 满了 。 反之，当栈 1 为空栈时， top2 等于 0 时，为栈 2 满。 但更多的情况，其实就是我刚才说的，两个栈见面之时，也就是两个指针之间相差 1 时，即 回top1 + 1 == top2 为栈满。

 

 

对于两栈共享空间的 push 方法，我们除了要插入乖素值参数外，还需要有一个判断是栈 1 还是栈 2 的栈号参数 stackNumber。插入元素的代码如下:

因为在开始已经判断了是否有栈满的情况，所以后面的 top+1 或 top2-1 是不担心溢出问题的。
对于两栈共享空间的 pop 方法，参数就只是判断栈1 栈2 的参数 S1ackNumber .
代码如下:

        事实上，使用这样的数据结构，通常都是当两个栈的空间需求有相反关系时，也就是一个栈增长时另一个栈在缩短的情况。

 

       就像买卖股票一样，你买入时，一定是有一个你不知道的人在做卖出操作 . 有人赚钱，就一定是有人赔钱。

       这样使用两栈共享空间存储方法才有比较大的意义 . 否则两个栈都在不停地增长，那很快就会因栈满而溢出了。

       当然，这只是针对两个具有相同数据类型的栈的一个设计上的技巧，如果是不相同数据类型的栈，这种办法不但不能更好地处理问题，反而会使问题变得更复杂，大家要注意这个前提。
 

3.1栈的链式存储结构

在栈的基础上加入链表的特性,栈的链式存储结构，简称为链栈。

 

因为有了栈顶,所以头结点已经没意义了,所以只有栈顶.

 

因为有链的特性,所以是不存在栈满这种情况,如果出现栈满的情况,说明内存太小了.

对于空栈来说，空链表原定义是头指针指向空 ， 那么链栈的空其实就是 top=NULL的时候。
 

链栈的操作绝大部分都和单链表类似，只是在插入和删除上，特殊一些。
 

3.2进栈操作

 

对于链栈的进栈 push 操作，假设元素值为 e 的新结点是 s ，top为栈顶指针，示意图如图 4-6-2 所示代码如下。
 

 

记住栈底下标为0,从栈底开始

 

3.3出栈操作

至于链栈的出栈 pop 操作，也是很简单的三句操作. 假设变量 p 用来存储要删除的栈顶结点，将栈顶指针下移一位，最后释放 p 即可，如图 4-6-3 所示。
 

链栈的进栈push和出站pop操作都很简单,没有循环操作,时间复杂度均为O(1).

 

小结

对比一下顺序栈与链栈，它们在时间复杂度上是一样的，均为 0(1)。对于空间性能， 顺序栈需要事先确定一个固定的长度，可能会存在内存空间浪费的问题，但它的优势是存取时定位很方便，而链栈则要求每个元素都有指针域，这同时也增加了一些内存开销，但对于栈的长度无限制。

       所以它们的区别和线性表中讨论的一样， 如果栈的使用过程中元素变化不可预料，有时很小，有时非常大，那么最好是用链栈，反之，如果它的变化在可控范围内，建议使用顺序棋会更好一些。

 

3.4栈的作用

       有的同学可能会觉得，用数组或链表直接实现功能不就行了吗?干吗要引入栈这样的数据结构呢?这个问题问得好。

       其实这和我们明明有两只脚可以走路，干吗还要乘汽车、火车、飞机一样。理论上，陆地上的任何地方，你都是可以靠双脚走到的，可那需要多少时间和精力呢?我们更关注的是到达而不是如何去的过程。

       栈的引人简化了程序设计的问题，划分了不同关注层次，使得思考范围缩小，更加聚焦于我们要解决的问题核心。反之，像数组等，因为要分散精力去考虑、数组的下标增减等细节问题，反而掩盖了问题的本质。

       所以现在的许多高级语言，比如 Java 、 C#等都有对栈结构的封装， 你可以不用关
注它的实现细节，就可以直接使用 Stack 的 push 和 pop 方法，非常方便 。

 

3.5栈的应用-递归

先看一个经典的递归例子:斐波那契数列也叫兔子数列

表中数字 1 ,1 , 2, 3 , 5, 8 , 13 . . ....构成了一个序列。这个数列有个十分明显的特点，那是:前面相邻两项之和，构成了后一项
之和.

打印出前40位兔子数,常规的迭代算法:

其实就是先预先占用40个内存单位,,将前两位之和填入新的变量中.

递归算法:

3.5.1递归定义

在高级语言中，调用自己和其他函数并没有本质的不同。我们把一个直接调用自己或通过一系列的调用语句间接地调用自己的函数，称做递归函数。

迭代和递归的区别是:迭代使用 的是循环结构，递归使用的是选择结构。递归能使程序的结构更清晰、更简洁、更容易让人理
解，从而减少读懂代码的时间。但是大量的递归调用会建立函数的副本，会耗费大量的时间和内存。迭代则不需要反复调用函数和占用额外的内存。
 

前面我们已经看到递归是如何执行它的前行和退回阶段的。递归过程退回的顺序是它前行顺序的逆序。在退回过程中，可能要执行某些动作，包括恢复在前行过程中存储起来的某些数据。

这种存储某些数据，并在后面又以存储的逆序恢复这些数据，以提供之后使用的需求，显然很符合栈这样的数据结构，因此 ， 编译器使用栈实现递归就没什么好惊讶的。
 

后面是一些关于栈的应用,就不写出来了,计算器,逆波兰算法.中缀表达式转后缀表达式,书名<<大话数据结构>>,第4.9章有兴趣的可以去翻书看下.

 

 

 

4.队列的定义

队列 ( queue ) 是只允许在一端进行插入操作，而在另一端进行删除操作的线性表。

队列是一种先进先出(First In First Out) 的线性表,简称FIFO,允许插入的一段称为队尾,允许删除的一端称为队头.

图示理解:

生活中的例子:

在用电脑时有没有经历过，机器有时会处于疑似死机的状态，鼠标点什么似乎都没用，双击任何快捷方式都不动弹。就当你失去耐心，打算重启时,突然它像酒醒了一样，把你刚才点击的所有操作全部都按顺序执行了一遍。这其实是因为操作系统中的多个程序因需要通过一个通道输出，而按先后次序排队等待造成的。

再比如像移动、联迪、电信等客服电话，客服人员与客户相比总是少数，在所有的客服人员都占线的情况下，客户会被要求等待，直到有某个客服人员空下来，才能让最先等待的客户接通电话。这里也是将所有当前拨打客服电话的客户进行了排队处
理。

操作系统和客服系统中，都是应用了一种数据结构来实现刚才提到的先进先出的排队功能，这就是队列。
 

常用方法:

循环队列

队列储存结构方式一样有两顺序和链式两种,先看看顺序.

前面讲过顺序线性表的缺点,当插入或删除非尾部元素时必须大量元素一起移动,但循环队列解决了这个问题.

 

如果不去限制队列的元素必须存储在数组的前 n 个单元这一条件，出队的性能就会大大增加。 也就是说，队头不需要一定在下标为 0 的位置 ， 如图 4-12-3 所示。
 

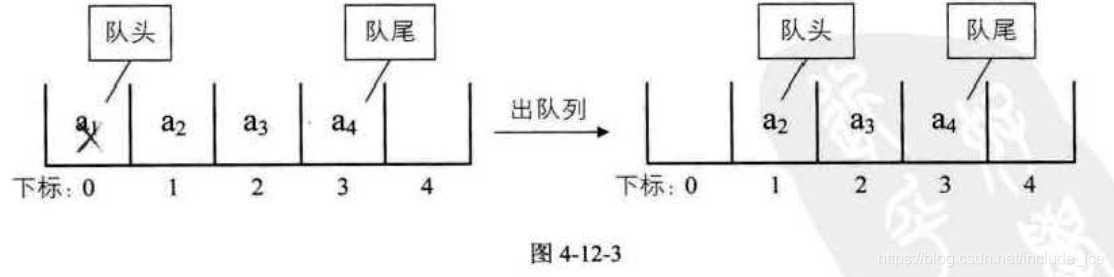
为了避免当只有一个元素时，队头和队尾重合使处理变得麻烦，所以引入两个指针， front 指针指向队头元素 ， rear 指针指向队尾元素的下一个位置，这样当 的nt 等于 rear 肘，此队列不是还剩一个元素，而是空队列 。
 

假设是长度为 5 的数组，初始状态，空队列如图 4-12-4 的左图所示， front 与rear 指针均指向下标为 0 的位置 。 然后入队 a1 、 a2 、 a3 、 a4 ， front 指针依然指向下标为 0 位置，而 rear 指针指向下标为 4 的位置，如图 4-12-4 的右图所示。
 

出队 al、 a2 ，则 front 指针指向下标为 2 的位置， rear 不变，如图 4-12-5 的左闺所示，再入队 a5，此时 front 指针不变， rear 指针移动到数组之外。嗯?数组之外 ，那将是哪里?如图 4-12-5 的右图所示。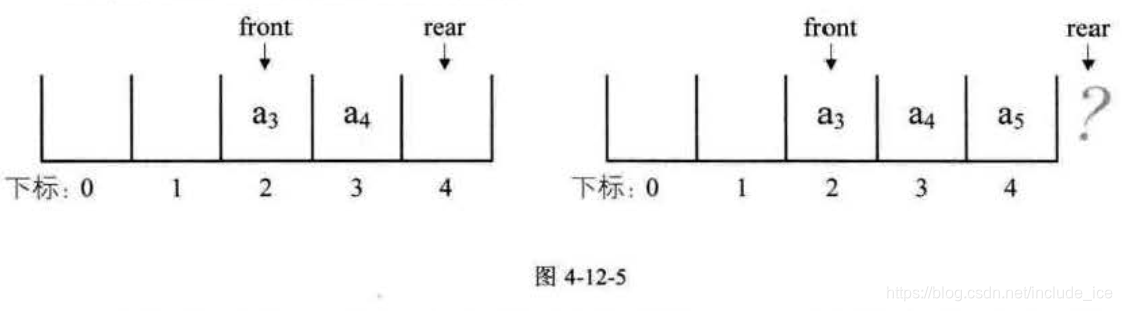

问题还不止于此。假设这个队列的总个数不超过5个，但目前如果接着人队的话，因数组末尾元素已经占用，再向后力日 ，就会产生数组越界的错误，可实际上，我们的队列在下标为 0 和 1 的地方还是空闲的 。 我们把这种现象叫做"假滥出 " 。

现实当中 ，你上了公交车，发现前排有两个空座位，而后排所有座位都已经坐满，你会怎么做?立马下车，并对自己说， 后面没座了 ，我等下一辆?没有这么笨的人，前面有座位，当然也是可以坐的，除非坐满了 ， 才会考虑下一辆。

所以解决假溢出的办法就是后面满了 ，就再从头开始，也就是头尾相接的循环。我们把队列的这种头尾相接的顺序存储结构称为循环队列。
 

刚才的例子继续，图 4-12-5 的 rear 可以改为指向下标为 0 的位置，这样就不会造成指针指向不明的问题了，如图 4-12-6 所示。
 

接着人队衔，将它放置于下标为 0 处， rear 指针指向下标为 1 处，如图 4-12-7的左图所示。若再入队a7，则 rear 指针就与front 指针重合，同时指向下标为 2 的位置，如图 4-12-7 的右图所示。
 

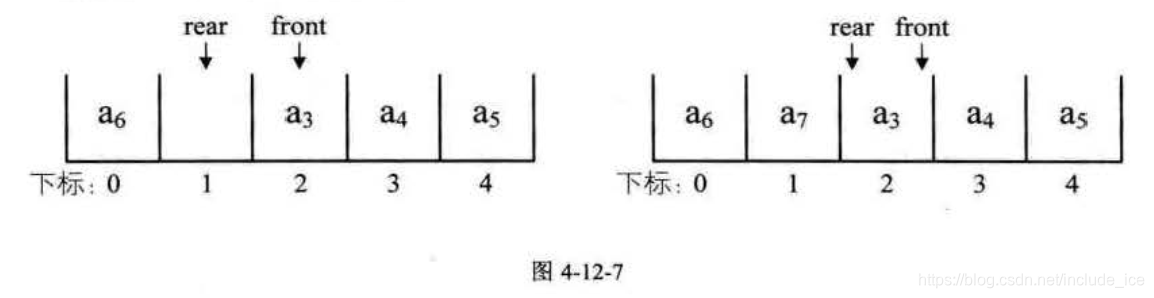
• 此时问题又出来了，我们刚才说，空队列时， fronr 等于此缸，现在当队列满时，也是 fro町等于 rear，那么如何判断此时的队列究竟是空还是满呢?

• 办法一是设置一个标志变量 flag ， 当front == rear ，且 flag = 0 时为队列空，当 front == rear，且 flag= 1 时为队列满。

• 办法二是当队列空时，条件就是 front = rear ，当队列满时，我们修改其条件，保留一个元素空间。也就是说，队列满时，数组中还有一个空闲单元。例如图 4-12-8 所示，我们就认为此队列已经满了，也就是说，我们不允许图4-12-7 的右图情况出现。
 

我们重点来讨论第二种方法，由于 rear 可能比 front 大，也可能比 front 小，所以尽管它们只相差一个位.琶时就是满的情况，但也可能是相差整整一圈 。

所以若队列的最大尺寸为 QueueSize ，那么队列满的条件是 (rear+l) % QueueSlze ==front (取模 "%" 的目的就是为了整合 rear 与 front 大小为一个问题)。

比如上面这个例子，QueueSize = 5 ，图 4-12-8 的左图中 front吨 ，而 rear=4 ， (4+1 ) %5 = 0 ，所以此时队列满. 再比如图 4-12-8 中的右图， front = 2 而 rear = 10 ( 1 + 1) %5 = 2 ，所以此时队列也是满的。而对于图 4-12-6 ， front=2 而 rear= 0 , (0+1) %5 = 1 , 1 '* 2 ，所以此时队列并没有满。
 

不理解以上这段话的可以计算一下,是刚好符合需求的.

另外，当 rear> front 时，即图 4-12-4 的右图和 4-12-5 的左图，此时队列的长度为 rear一front 但当 rear < front 时，如图 4-12-6 和图 4-12-7 的左图，队列长度分为两段 ， 一段是 QueueSize- front， 另一段是 0 + rear，加在一起，队列长度为rear-front + QueueSize。因此通用的计算队列长度公式为:
(rear- front + QueueSize) %QueueSize
有了这些讲解，现在实现循环队列的代码就不难了。
 

从这一段讲解，大家应该发现，单是顺序存储，若不是循环队列，算法的时间性能是不高的，但循环队列又面临着数组可能会溢出的问题，所以我们还需要研究一下不需要担心队列长度的链式存储结构。
 

队列的链式存储结构及实现

队列的链式存储结构，其实就是线性表的单链表，只不过它只能尾进头出而已，我们把它简称为链队列。
 

为了操作上的方便，我们将队头指针指向链队列的头结点，而队尾指针指向终端结点，如图 4-13-1 所示。

空队列时， front 和 rear 都指向头结点，如图 4-13-2 所示。

注意这里有了头结点的存在.

链式队列的入队操作:

入队操作时，其实就是在链表尾部插入结点.

出队操作:

出队操作时，就是头结点的后继结点出队，将头结点的后继改为它后面的结点，若链表除头结点外只剩一个元素时，要出队 则需将 rear 指向头结点，如图 4-13-4 所示。

对于循环队列与链队列的比较，可以从两方面来考虑，从时间上，其实它们的基本操作都是常数时间，即都为 O(1)的，不过循环队列是事先申请好空间，使用期间不释放，而对于链队列，每次申请和释放结点也会存在一些时间开销，如果入队出队频
繁，则两者还是有细微差异。对于空间上来说，循环队列必须有一个固定的长度，所以就有了存储元素个数和空间浪费的问题。而链队列不存在这个问题，尽管它需要一个指针域， 会产生一些空间上的开销，但也可以接受 。 所以在空间上，链队列更加灵活。

总的来说，在可以确定队列长度最大值的情况下 ，建议用循环队列，如果你无法预估队列的长度时，则用链队列。
 

 

这一章讲的是栈和队列，它们都是特殊的线性表，只不过对插入和删除操作做了限制 。
栈 ( stack) 是限定仅在表尾进行插入和删除操作的线性表。

队列 ( queue) 是只允许在一端进行插入操作，而在另一端进行删除操作的线性表。
它们均可以用线性表的顺序存储结构来实现，但都存在着顺序存储的一些弊端。
 

因此它们各自有各自的技巧来解决这个问题。
对于楼来说，如果是两个相同数据类型的栈，则可以用数组的两端作栈底的方法来让两个栈共享数据，这就可以最大化地利用数组的空间。
对于队列来说，为了避免数组插入和删除时需要移动数据，于是就引入了循环队列 ，使得队头和队尾可以在数组中循环变化。解决了移动数据的时间损耗，使得本来插入和删除是 O(n)的时间复杂度变成了 O(1) 。
 

它们也都可以通过链式存储结构来实现，实现原则上与线性表基本相同

 

本章结束,谢谢.