算法与数据结构-第三章：线性表

线性表 ( list ):零个或多个数据元素的有限序列。

例子：一个班级的小朋友，一个跟着一个排着队，有一个打头，有一个收尾，这样如同有一根线把他们串联起来了，就可以称之为线性表。

线性表的创建、添加、删除这种基础功能就不说了。

首先，线性表有两种存储结构：

1.顺序存储结构。

2.链式存储结构。

 

 

1.顺序存储结构：

线性表的顺序存储结构，指的是用一段内存地址连续的存储单元依次存储线性表的数据元素。

说通俗点：就是在内存中找了块地，通过占位的形式，把一定内存空间给占了， 然后把相同数据类型的数据元素依次存放在这块空地中，在高级语言中顺序存储结构体现为数组。
 

内存中的地址，就和图书馆或电影院里的座位一样，都是有编号的。

存储器中的每个存储单元都有自 己的编号，这个编号称为地址。

当我们占座后，占座的第一个位置确定后，后面的位置都是可以计算的 。

编写获得元素值，插入元素，删除元素的功能时要注意大多数语言都是从0开始计数。

 

插入功能思路：

刪除功能思路：

线性存储结构的优缺点

 

2. 线性表的链式存储结构

 

链式存储结构又分为单向链和双向链

在上面的顺序结构中，每个数据元素只需要存数据元素信息就可以了。现在链式结构中 ，除了要存数据元素信息外 ， 还要存储它的后继元素的存储地址。
 

为了表示每个数据元素 ai 与其直接后继数据元素 ai+1 之间的逻辑关系 ， 对数据元素来说 ， 除了存储其本身的信息之外，还需存储一个指示其直接后继的信息(即直接后继的存储位置)。我们把存储数据元素信息的域称为数据域 ， 把存储直接后继位置的域称为指针域。 指针域中存储的信息称做指针或链。 这两部分信息组成数据元素 ai 的存储映像，称为结点 (Node) 。

先讲单链。

 

单向链表

n 个结点 ( ai 的存储映像) 链结成一个链表，即为线性表 ( a1 ， a2,… , an ) 的链
式存储结构，因为此链表的每个结点中只包含一个指针域，所以叫做单链表。
 

双向链表稍后讲

 

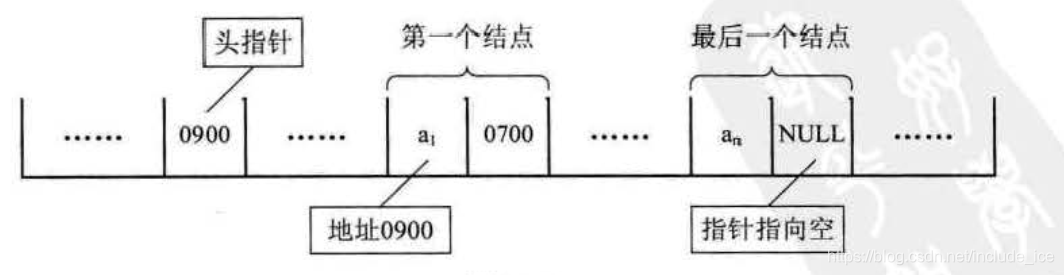
单向链表图示结构：

 

 

 

链表中第一个结点的存储位置叫做头指针，那么整个链表的存取就必须是从头指针开始进行了 。

之后的每一个结点，其实就是上一个的后继指针指向的位置。

线性链表的最后一个结点指针为"空''，因为最后一个结点没有后续结点了，所以没法指向下一个结点，所以为空。

如下图：
 

 

有时，我们为了更加方便地对链装进行操作，会在单链表的第一个结点前附设一个结点，称为头结点。

头结点的数据域可以不存储任何信息 ，谁叫它是第1个呢，所以有这个特权，也可以存储存线性表的长度等附加信息，头结点的指针域存储指向第一个结点的指针。
如下图：

头指针和投结点的异同：

图示补充理解：

空表:

 

非空表:

可以没有头结点

 

 

线性表链式存储结构代码描述
 

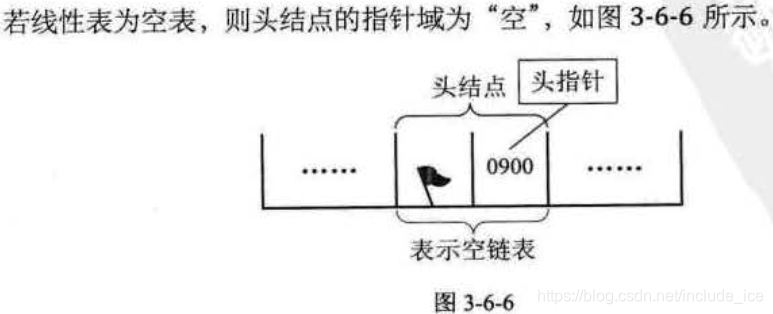
因为没有后续节点，所以头指针为空。

 

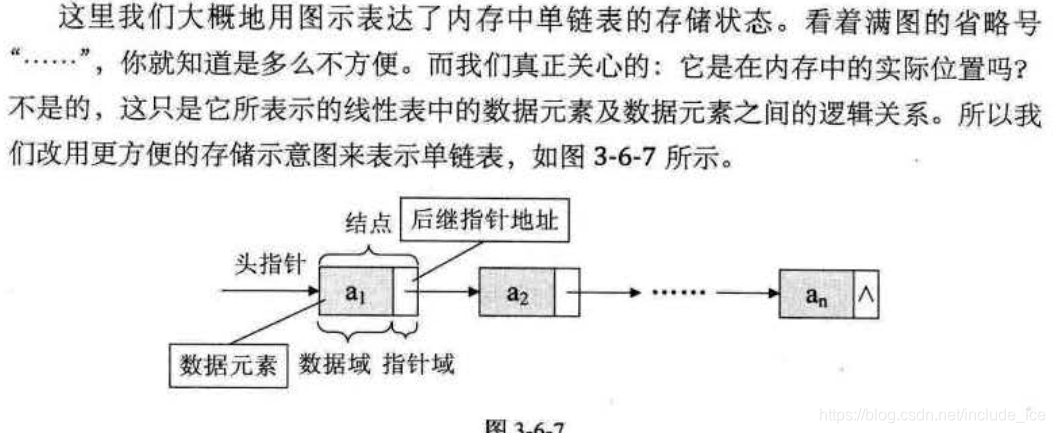
结点由存放数据元素的数据域和存放后继结点地址的指针域组成。
 

3.单链表的读取

 

在线性序存储结构中，我们要计算任意一个元素的存储位置是很容易的。但在单链表中，由 于第 i 个元素到底在哪?没办法一开始就知道，必须得从头开始找。因此，对干单链表实现获取第 i 个元素的数据的操作 GetElem ，在算法上，相对要麻烦一些。
 

获得链表第 i 个数据的算法思路:
1. 声明一个结点 p 指向链表第一个结点，初始化 j 从 1 开始;
2. 当 j<i 时，就遍历链裴，让 p 的指针向后移动，不断指向下一结点， j 累加 1;
3. 若到链表末尾 p 为空，则说明第 i 个元素不存在;
4 . 否则查找成功，返回结点 p 的数据 。
 

 

说白了，就是从头开始找，直到第 i 个元素为止。由于这个算法的时间复杂度取决于 i 的位置，当 i=1 时，则不需遍历，第一个就取出数据了，而当 i=n 时则遍历 n-1次才可以。 因此最坏情况的时间复杂度是 O(n) 。

由于单链表的结构中没有定义表长，所以不能事先知道要循环多少次，因此也就不方便使用 for 来控制循环。其主要核心思想就是 "工作指针后移' ，这其实也是很多算法的常用技术。
 

4.单链表的插入与删除

4.1单链表的插入

先看插入,我说的简单易懂一些,例子:

假设有一个单链表A1:其原本元素为:A-C-D-E-F

现在要在A和C之间插入一个B,那么我们只需要修改A的指针域和B的指针域就ok.

用图来表示

 

4.2单链表的删除

删除例子:

删除E,修改D中的指针域就ok.

4.3 单链表整表的创建

单链表创建的算法思路 :
1. 声明一结点 p 和计数器变量 i ;
2. 初始化一空链表 L;
3. 让 L 的头结点的指针指向 NULL ，即建立一个带头结点的单链表 ,这里空表创建完成;
4. 循环 :
• 生成一新结点赋值给 p;
• 随机生成一数字赋值给 p 的数据域 p->data;
• 将 p 插入到头结点与前一新结点之间。

上面用的是插队排序.

4.4单链表的删除

单链表整表删除的算法思路如下:
1. 声明一结点 p 和 q ;
2. 将第一个结点赋值给 p;
3 . 循环:
• 将下一结点赋值给 q;
• 释放 p;
• 将 q 赋值给 p 。
 

4.5单链表结构与顺序存储结构的优缺点

来个简单的说明吧:

顺序表:长度不可变,快速查找,增删效率低.

单向链表:长度可变,龟速查找,增删效率高.

不同情景不同选择.

 

 

5.静态链表

之所以叫静态链表,是因为:既有顺序表的静态特性,也有链表的特性.

我直接将书里面的说明截图过来,我觉得已经解释的够简单清晰了.

 

 

先标记一下基础:

未插入元素的数组称为备用链表.

数组的第一个元素的''指针''用于存放备用链表的第一个结点的下标.

数组的最后一个元素的''指针''用于存放已用表的第一个结点的下标,相当于头结点.

静态链表在逻辑上的顺序为,头结点,第一个元素,第一个结点.

图示辅助理解:

 

书中原本描述是cur对应"指针",data对应数据域.

 

5.1静态链表的优缺点

 

优点:增删方便,因为不需要移动大量元素.

缺点:最大长度固定,注意是最大长度,因为本质上依旧是数组.

 

6.循环链表

将单链表中终端结点的指针由空指针改为指向头结点，就使整个单链表形成一个环，这种头尾相接的单链表称为单循环链表，简称循环链表 ( circular linkedlist) 。
 

 

空的循环链表:

非空循环链表:

 

7.双向链表

单向链表只能单向历遍,双向链表可以双向历遍.

在单链表中，有了 next 指针，这就使得要查找下一结点的时同复杂度为0(1) 。可是如果要查找的是上一结点的话，那最坏的时间复杂度就是 O(n)了，因为每次都要从头开始遍历查找。
 

为了克服单向性这一缺点，科学家设计出了双向链表。双向链表(duble linked list) 是在单链表的每个结点中，再设置一个指向其前驱结点的指针域。所以在双向链表中的结点都有两个指针域， 一个指向直接后继，另一个指向直接前驱。
 

图示辅助理解:

7.1双向循环链表

直接上图:空表

非空表

双向链表是单链表中扩展出来的结构，所以它的很多操作是和单链表相同，比如求长度的 ListLength ，查找元素的 GetElem ，获得元素位置的 LocateElem 等，这些操作都只要涉及一个方向的指针即可，另一指针多了也不能提供什么帮助。
 

增删元素操作时会多一个步骤,因为要修改前后两个指针.

 

8.总结

线性表的这两种结构是后面其他数据结构的基础，把它们学明白了，对后面的学习有着至关重要的作用。
 

 

第三章完结~