【原创】《矩阵的史诗级玩法》连载二十四：两条贝塞尔曲线的常规求解方法（上）

拖延症开始慢慢发作了，这次主要是工作压力变大，而且虽然我某方面的技术优于不少同事，但综合能力却比不过大多数人。有个需求，产品那边一开始就想错了，很多写程序的都提出了质疑，但我没有提出，这原因除了我不懂得思考以外，还有很关键的一点是，按照产品的做法，技术难度比正确的做法高出了几个数量级。而对于我这种技术狂人来说，有难度并且在我感兴趣范围内的东西我都特别喜欢，所以我就欣然接受了产品提出来的做法。再者，这个项目已经拖了3年没出成果，所以我更加坚信，产品的想法是正确的，如果是按着正确的做法来，那应该早两年就能做出来了，而不用一直拖到今天。

然而就在这周，我很绝望地在数学上证明了产品的做法是无解的，然后产品再去做了调研，终于发现了问题所在。但不管怎样，我还是很感谢这位产品给我出的这道很有意思的难题。虽然我下周开始要重做，但是在这3个月里，我感觉到自己技术水平又提高了一个档次，而坏处自然就是要赶工了。所幸需求调整后，技术难度降低了很多。

废话完了，开始正题。

上篇我们用常规方法计算二次贝塞尔曲线和直线的交点，发现也不比矩阵法复杂多少，这当中的原因，是直线让我们钻了个空子，所以求解才会这么轻松。而矩阵法中，也有一段代入是因为直线的存在而变得简单。大家可以在连载二十一中找到这样的一段演算过程。

如果这不是简单的直线方程，那么代入也是很蛋疼的。

因此我们尚未能确定如果求交的都是二次贝塞尔曲线，谁的优势会更大。本文我们先来看看常规求解的做法。

我们来求一下这两条曲线的交点，其中已知

第一条曲线的3个关键点分别为：(-1, -1)，(2, 2)，(1, -0.5)，

第二条曲线的3个关键点分别为：(3, 0.5)，(-3, 2)，(2, -1)。

 

先说一下，这里解出来的数字不会像之前直线和贝塞尔曲线求交那么整齐，因为四次方程我没有在学校学过，也就没做过题目，所以不懂得凑数字的套路，也懒得去凑了。反正扔给4次方程求解的类来就是。

我们先把方程列出来。根据连载十七给出的系数计算公式

可以直接给出两条方程关于t的二次三项式分别为：

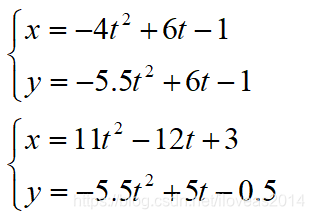
看起来都是二次方程，求解并不复杂，但是从上面的效果图来看，交点却达到了4个，那这个结果是怎么来的呢？我的QQ群里曾经讨论过这个问题，他们有的人说，这还不简单，x一道二次方程，y一道二次方程，合起来不就是4个解了吗？我很困惑，继续追问，得到的答案我也是醉了。

由

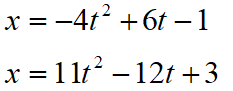
得到

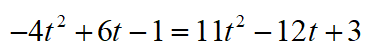
类似地有

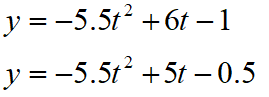
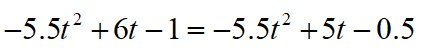
两个关于t的一元二次方程分解解出两个解，因此最多能产生4个交点。

这解释还真是非常完美，在闲聊场合会让人感觉到深入浅出，简单明了而不失逼格。实际上这种做法完全错误，但如果我当场指出问题所在的话，相信不少人会给我来一句“太认真你就完了”。

嗯，闲聊是不用认真，但解决问题就不一样了，不给出正确结果誓不罢休。那我们就来看看这个做法到底错在哪里。

为了更容易看出问题所在，我们换成一次贝塞尔曲线，也就是直线来做个测试。

第一条直线过(0,0)和(2,2)，第二条直线过(0, 1)和(1, 0)

套用一次贝塞尔曲线的方程

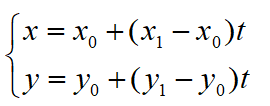
得到第一条方程为

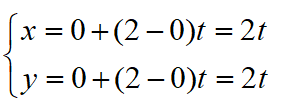
第二条方程为

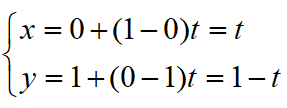
接着我们用跟上面一样的思路，x建立一条方程，得到

再对y建立一条方程，得到

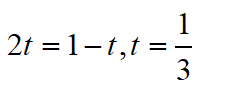
我们知道，两直线最多一个交点，所以这个结果多半是错的，但是有人还不死心，可能是增根，去掉一个就好了。那好吧，我们代入一下看看。

t=0代入第一条方程，得到x=0，y=0，代入第二条方程，得到x=0，y=1，这显然不是交点，两条方程算出来的xy都不一致。

然后t=1/3，第一条方程是x=1/3，y=1/3，第二条方程是x=1/3，y=2/3，也不对。

可见这个方法确实有问题，那我们用常规做法（普通方程）来解一下吧。

第一条直线的普通方程为y=x，第二条直线的普通方程为y=1-x

解得x=1/2，y=1/2

然后，我们试着把t求回来，对于第一条方程，有

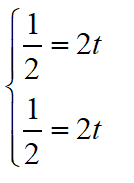
得到t=1/4

对于第二条方程，有

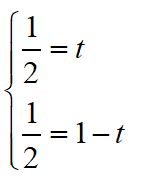
得到t=1/4

至此真相大白了！虽然两条参数方程都用字母t来表示参数，但在交点处，它们的t并不相等，所以不能把两个方程里的t视为同一个未知数进行求解。也就是说，上面的两条贝塞尔曲线方程的本质是这个样子。

这里面，黑色的t和紫色的t是两个不同的未知数，它们的值不相等，不能混在一起求解。

因此，用常规做法，沟通它们的桥梁仍然只有x和y，所以要消掉其中一条方程中的t，然后代入到另一条方程中。其繁琐程度可见一斑。

然而这篇我又写长了，此处我再发点牢骚。我再苦口婆心地给群里人讲解这个，他们也不以为意，反正自己用不到，没必要深挖，真用到了，大不了找现成库，大不了找别人（比如我）来帮忙解决，细节他们不用关心，但做好了却能成为他们吹牛逼的资本。拿前面的那种错误解法忽悠下别人，立马就变身为大神了。不过我相信，懂我的人总能找得到，在三维家就有好几个了，所以牢骚模式到底为止。

消t的蛋疼过程，我放到下一篇去，以免本篇太长。