初识AdaBoost

AdaBoost

martin

---

AdaBoost是典型的Boosting方法，并且效果很显著。下图是AdaBoost的框架图：

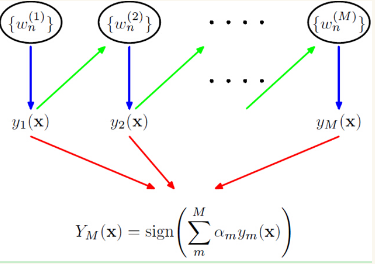
算法过程

下面介绍AdaBoost算法的过程：
1. 初始化训练数据的权值分布：

$$D_1 = (w_{11},w_{12},w_{13},...,w_{1N}),w_{1i}={1\over N},i=1,2,...,N$$

2. 对$m=1,2,...,M$
(a) 使用具有权值分布$D_m$的训练集学习，得到基本分类器：

$$G_m(x):X->\{-1,+1\}$$
(b) 计算 $G_m(x)$在训练数据集上的分类误差：
$$e_m = P(G_m(x_i)\not=y_i)={\sum_{i=1}^Nw_{mi}I(G_m(x_i)\not=y_i)\over \sum_{i=1}^Nw_{mi}}=\sum_{i=1}^Nw_{mi}I(G_m(x_i)\not=y_i)$$
$$上式中，\sum_{i=1}^Nw_{mi}=1$$
(c) 计算 $G_m(x)$的系数：
$$\alpha_m = {1\over 2}log{{1-e_m}\over e_m}$$
(d) 更新数据集的权值分布：
$$D_{m+1} = (w_{m+1,1},w_{m+1,2},...,w_{m+1,N})$$
$$w_{m+1,i} = {w_{mi}\over Z_m}e^{-\alpha_my_iG_m(x_i)}$$
$$其中，Z_m = \sum_{i=1}^Nw_{mi}e^{-\alpha_my_iG_m(x_i)}，是规范化因子$$
(e) 重复 $(a)-(d)$步 $m$次得到$m$个权值 $a$和$m$个基分类器 $G(x)$

3. 构建基本分类器的线性组合：

$$f(x) = \sum_{m=1}^Ma_mG_m(x)$$
4. 最终得到分类器：
$$G(x) = sign(f(x)) = sign(\sum_{m=1}^{M}a_mG_m(x))$$

基分类器权值$a$与训练数据集权值$w$的分析

1. 先来看基分类器的权值$\alpha$，公式如下:

$$\alpha = {1\over 2}log{{1-e_m}\over e_m}$$

我们知道AdaBoost是将多个弱分类器组合起来形成一个很强的分类器，但这里有个隐含条件：弱分类器。什么叫弱分类器？意思就是在效果上比随机猜想要好的分类器。比如二分类问题，随机猜想的正确率是0.5，所以说弱分类器的正确率一定要比0.5高，于是它的错误率$e_m<0.5$，所以$\color{red}{\alpha会随着e_m的减小而增大}$，这是什么意思？意思是，如果我的基分类器的错误率很小，也就是正确率很大，那么在众多基分类器中我给予它很大的权值$\alpha$，让它能发挥更大的作用。

2. 再来看训练数据集分布的权值分配，公式如下：

$$w_{m+1,i} = {w_{m,i}\over Z_m}e^{-a_my_iG(x_i)}= \left\{ {\text{${w_{m,i}\over Z_m}e^{-a_m}$，$G_m(x_i)=y_i$}\atop \text{${w_{m,i}\over Z_m}e^{a_m}$，$G_m(x_i)\not=y_i$}} \right.$$

由公式可知，对训练集的样例正确分类与错误分类之间，错误分类样本的权值被放大：$e^{2\alpha_m} = {{1-e^m}\over e^m}$倍，所以，在下一轮学习中将会被更大关注。

AdaBoost推导

AdaBoost模型是由基本分类器组成的$\color{red}{加法模型}$，损失函数是$\color{red}{指数函数}$。

1. 加法模型：$f(x) = \sum_{m=1}^M\alpha_mG_m(x)$

2. 损失函数：$L(y,f(x)) = e^{-yf(x)}$

3. 每次训练后的基分类器都是乘以$\alpha$再与前一个模型线性相加，所以对于第$m-1$次训练后模型为：

$$\begin{align} f_{m-1} &= f_{m-2}+\alpha_{m-1}G_{m-1}(x)\\ & = \alpha_1G_1(x)+...+\alpha_{m-1}G_{m-1}(x)\\ \end{align}$$

4. 于是，在第$m$次训练后有：$f_m(x) = f_{m-1}(x)+\alpha_mG_m(x)$

5. 目标是每一次的损失在训练集上最小，所以最小化目标函数为：

$$\begin{align} (\alpha_m,G_m(x)) &= min\sum_{i=1}^Ne^{-y_if_m(x_i)}\\ & = min\sum_{i=1}^Ne^{-y_i[f_{m-1}(x_i)+\alpha_mG_m(x)]}\\ & = min\sum_{i=1}^Ne^{-y_if_{m-1}(x_i)-y_i\alpha_mG_m(x)}\\ & = min\sum_{i=1}^Nw_{mi}e^{-y_i\alpha_mG_m(x)}\\ \end{align}$$

上式中，将$e^{-y_if_{m-1}(x_i)}=w_{mi}$，因为$w_{mi}$既不依赖$\alpha$也不依赖与$G$，所以与最小无关。

6. 于是，有：

$$\begin{align} min\sum_{i=1}^Nw_{mi}e^{-y_i\alpha_mG_m(x)} & = min\sum_{y_i=G_m(x_i)}w_{mi}e^{-a}+\sum_{y_i\not=G_m(x_i)}w_{mi}e^a\\ & = min(e^{-a}\sum_{i=1}^Nw_{mi}I(y_i=G_m(x_i))+e^\alpha\sum_{i=1}^Nw_{mi}I(y_i\not=G_m(x_i)))\\ &=min(e^{-a}\sum_{i=1}^Nw_{mi}[1-I(y_i\not=G_m(x_i))]+e^\alpha\sum_{i=1}^Nw_{mi}I(y_i\not=G_m(x_i)))\\ & = min((e^\alpha-e^{-\alpha})\sum_{i=1}^Nw_{mi}I(y_i\not=G_m(x_i))+e^{-a}\sum_{i=1}^Nw_{mi}) \end{align}$$

所以，我们得到了优化的目标函数：

$$L(\alpha) = (e^\alpha-e^{-\alpha})\sum_{i=1}^Nw_{mi}I(y_i\not=G_m(x_i))+e^{-a}\sum_{i=1}^Nw_{mi}$$

7. 对6中的目标函数关于$\alpha$求导，令$\color{red}{\partial L(\alpha)\over \partial\alpha }=0$，求的最小值：

$${\partial L(\alpha)\over \partial\alpha} = -e^{-a}\sum_{i=1}^Nw_{mi}+(e^\alpha+e^{-\alpha})\sum_{i=1}^Nw_{mi}I(y_i\not=G_m(x_i))=0$$

等价于：

$$(e^\alpha+e^{-\alpha})\sum_{i=1}^Nw_{mi}I(y_i\not=G_m(x_i))=e^{-a}\sum_{i=1}^Nw_{mi}$$

因为：$e_m = \sum_{i=1}^Nw_{mi}I(y_i\not=G_m(x_i))$，$\sum_{i=1}^Nw_{mi}=1$

所以有：

$$(e^\alpha+e^{-\alpha})e_m = e^{-a}$$
等价于：
$$e^{2a} = {{1-e^m}\over e^m}$$
解得：
$$\alpha = {1\over 2}ln{{1-e^m}\over e^m}$$

8. 由于之前有个假设：$w_{mi}=e^{-y_if_{m-1}(x_i)}$，而这个式子又可以化为：

$$\begin{align} w_{m+1,i}&=e^{-y_if_{m}(x_i)}\\ & = e^{-y_i[f_{m-1}(x_i)+\alpha_mG_m(x_i)]}\\ & = w_{mi}e^{-y_i\alpha_mG_m(x_i)}\\ \end{align}$$

于是，就有了更新公式：

$$w_{m+1,i} = w_{mi}e^{-y_i\alpha_mG_m(x_i)}$$ ，与AdaBoost算法中的更新公式只差了个规范化因子而已。

参考：
[1] 《统计学习方法》李航