插入排序:
void InsertSort(int* arr , int n) {
// n是数组元素的个数
for(int i = 1; i < n; ++i) {
int num = *(arr+i);
for(int j = i-1; j >=0; j--) {
if(*(arr+j) > num) {
*(arr+j+1) = *(arr+j);
if(j == 0) {
arr[0] = num;
break;
}
}
else {
*(arr+j+1) = num;
break; // 表示此趟排序结束
}
}
}
}
void InsertSort(int arr[], int n)
{
for(int i = 0; i < n-1; ++i)
{
int end = i; // [0,end] 为有序数组
int tmp = arr[end+1]; // 将下标为end+1的元素插入到前面的数组中
while(end>=0)
{
if(tmp < arr[end])
{
arr[end+1] = arr[end];
}
else
{
break;
}
end--;
}
arr[end+1] = tmp;
}
}
看动图是最直观,最容易回忆起来的。
插入排序:当数组的前n个数据有序时,插入一个新的数据x,只需将x与n-1 n-2 n-3 ... 2 1 0下标的元素逐个比较(并不一定全部比较),当与arr[i]比较时,当元素比x大时,将元素后移一位,即arr[i+1] = arr[i],此时i下标的位置就空余出来了,将x再与arr[i-1]比较,如果大于等于arr[i-1] 则将x赋值给arr[i]即可,即那个小于等于x的元素的下一个位置。 综合,也就是元素大于x,则元素后移,元素小于等于x,x大于等于这个元素时,则将x放至元素后面。(也因此插入排序是一个稳定的排序)不过要注意比arr[0]小的情况。
插入排序的过程非常像抓扑克牌的过程,不过是从0开始抓起,一张新牌,我们可以直接看出这张牌应该放在哪个位置,但是计算机中的插入排序时,需要一一比较,找到合适的位置再插入。
综合一句话就是:当插入第i(i>=1)个元素时,前面的array[0],array[1],…,array[i-1]已经排好序,此时用array[i]的排序码与 array[i-1],array[i-2],…的排序码顺序进行比较,找到插入位置即将array[i]插入,(插入的位置就是他前面的元素小于等于他)原来位置上的元素顺序后移。 ..好像上面有点废话了
插入排序的特性总结:
1. 元素集合越接近有序,直接插入排序算法的时间效率越高
2. 时间复杂度:O(N^2)
3.当集合接近有序或完全有序时,插入排序时间复杂度接近O(N)
4. 空间复杂度:O(1)
5. 稳定性:稳定 它是一种稳定的排序算法
希尔排序
因为插入排序的第三个特点,所以产生了希尔排序。
希尔排序高效的原因就是:用比较少的时间将集合排为接近有序,最后再插入排序时,即为接近O(N)。
void ShellSort(int* arr,int n)
{
// 主要是针对数据量大的时候。
int gap = n;
// gap>1时为预排序,gap==1时为直接插入排序。
while(gap > 1){
gap = gap / 3 + 1;
// 这是一次全排序,间距为gap,当gap变为1时,就是直接插入排序了。结果为完全有序。
for(int i = 0; i <= n-gap-1; ++i) {
int end = i;
int tmp = arr[i+gap];
while(end >= 0) {
if(tmp < arr[end]) {
arr[end + gap] = arr[end];
}else{
break;
}
end-=gap;
}
arr[end+gap] = tmp;
}
}
}
当gap不为1时,都为预排序。而gap = gap/3+1; 使得gap最后一次循环时,一定是直接插入排序。
代码的核心是那个for循环,过段时间忘了之后可能这里的gap是最难理解的。
其实就相当于把直接插入排序的1换为gap。
for循环的意思是:整个集合中间距为gap的是一组,每一组进行直接插入排序,当然还是那个过程:保证前两个有序,插入第三个,保证前三个有序,插入第四个。只不过这里的第x与第x+1个之间间距为gap。而将这几组的插入排序合并起来就是这个for循环。 就是几个组轮流进行一次插入元素。
i <= n-gap-1是因为,最后的元素是n-gap-1 则下一个插入的元素就是n-gap-1+gap = n-1 即数组的最后一个元素,在它的那一组进行插入。 至此为一次预排序。
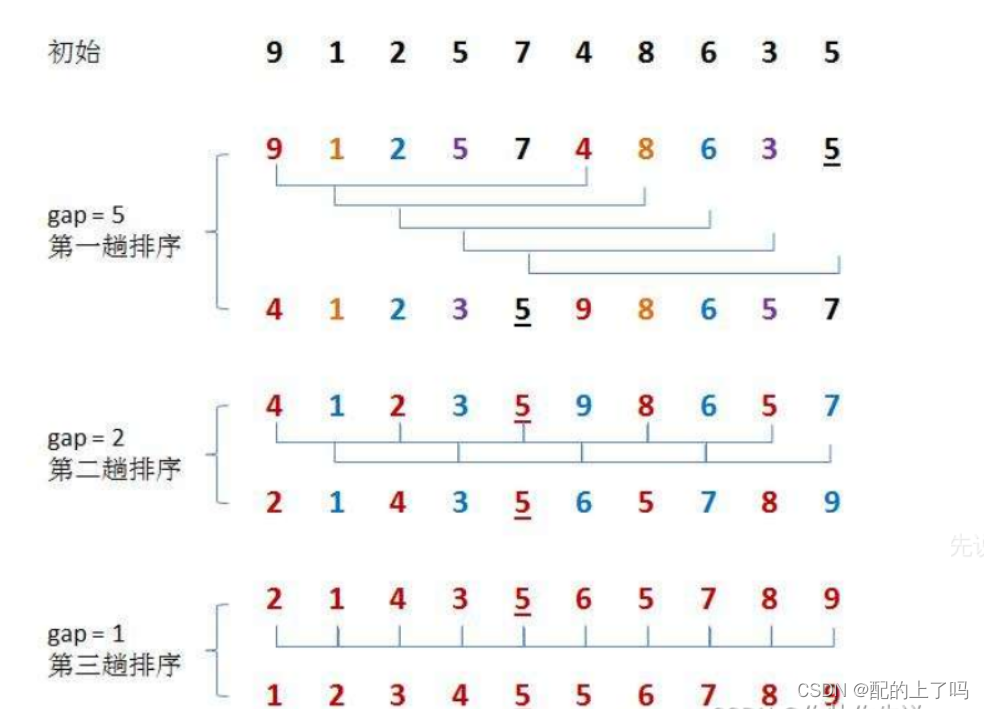
希尔排序的特性总结:
gap越大预排越快,预排后越不接近有序
gap越小预排越慢,预排后越接近有序时间复杂度: 大约O(N^1.3) (比较复杂
空间复杂度:O(N)
稳定性:不稳定,因为预排序的时候,一组数据中关键值相同的元素可能分到不同的组里面了。
闲聊:
刚才因为要写排序的博客,所以回顾了一下之前写的堆排序的blog。效果还是不错的,记忆模糊的主要原因是把topk和堆排混了,最重要的还是去理解向上调整和向下调整。再就是完全二叉树的一些特性,比如子节点和双亲结点在堆中的下标关系。最后就是向上调整和向下调整在堆排和topk中是如何使用的。





 本文详细解读了插入排序算法的工作原理及其优缺点,随后介绍了希尔排序的改进方法,重点讲解了预排序思想和时间复杂度优化。通过生活实例和代码演示,阐述了两种排序算法在不同场景的应用和性能提升。
本文详细解读了插入排序算法的工作原理及其优缺点,随后介绍了希尔排序的改进方法,重点讲解了预排序思想和时间复杂度优化。通过生活实例和代码演示,阐述了两种排序算法在不同场景的应用和性能提升。
















 6864
6864

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








