洛谷P1039 [NOIP2003提高组]侦探推理

最新推荐文章于 2025-07-23 20:59:04 发布

原创最新推荐文章于 2025-07-23 20:59:04 发布 · 1.4k 阅读

21 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #python #枚举法 #逻辑推理 #侦探推理 #程序设计

文章介绍了一个利用逻辑和编程解决的推理游戏，通过分析N个说谎者和真实证词，确定唯一罪犯。

题目描述

明明同学最近迷上了侦探漫画《柯南》并沉醉于推理游戏之中，于是他召集了一群同学玩推理游戏。游戏的内容是这样的，明明的同学们先商量好由其中的一个人充当罪犯（在明明不知情的情况下），明明的任务就是找出这个罪犯。接着，明明逐个询问每一个同学，被询问者可能会说：

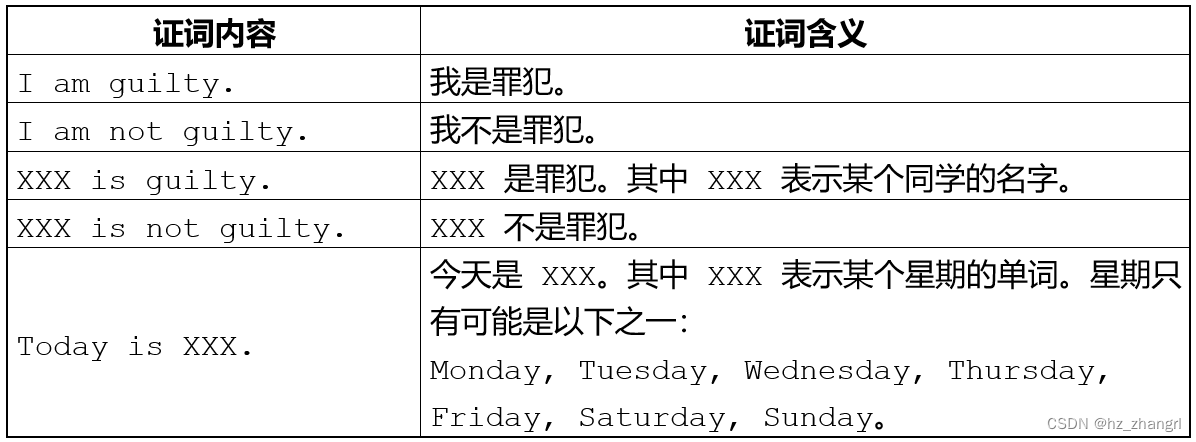
证词中出现的其他话，都不列入逻辑推理的内容。

明明所知道的是，他的同学中有 N 个人始终说假话，其余的人始终说真。

现在，明明需要你帮助他从他同学的话中推断出谁是真正的罪犯，请记住，罪犯只有一个！

输入格式

输入由若干行组成。

第一行有三个整数，M, N 和P。M是参加游戏的明明的同学数，N是其中始终说谎的人数，P是证言的总数。

接下来M行，每行是明明的一个同学的名字（英文字母组成，没有空格，全部大写）。

往后有P 行，每行开始是某个同学的名宇，紧跟着一个冒号和一个空格，后面是一句证词，符合前表中所列格式。证词每行不会超过 250个字符。

输入中不会出现连续的两个空格，而且每行开头和结尾也没有空格。

输出格式

如果你的程序能确定谁是罪犯，则输出他的名字；如果程序判断出不止一个人可能是罪犯，则输出 Cannot Determine；如果程序判断出没有人可能成为罪犯，则输出 Impossible。

输入输出样例

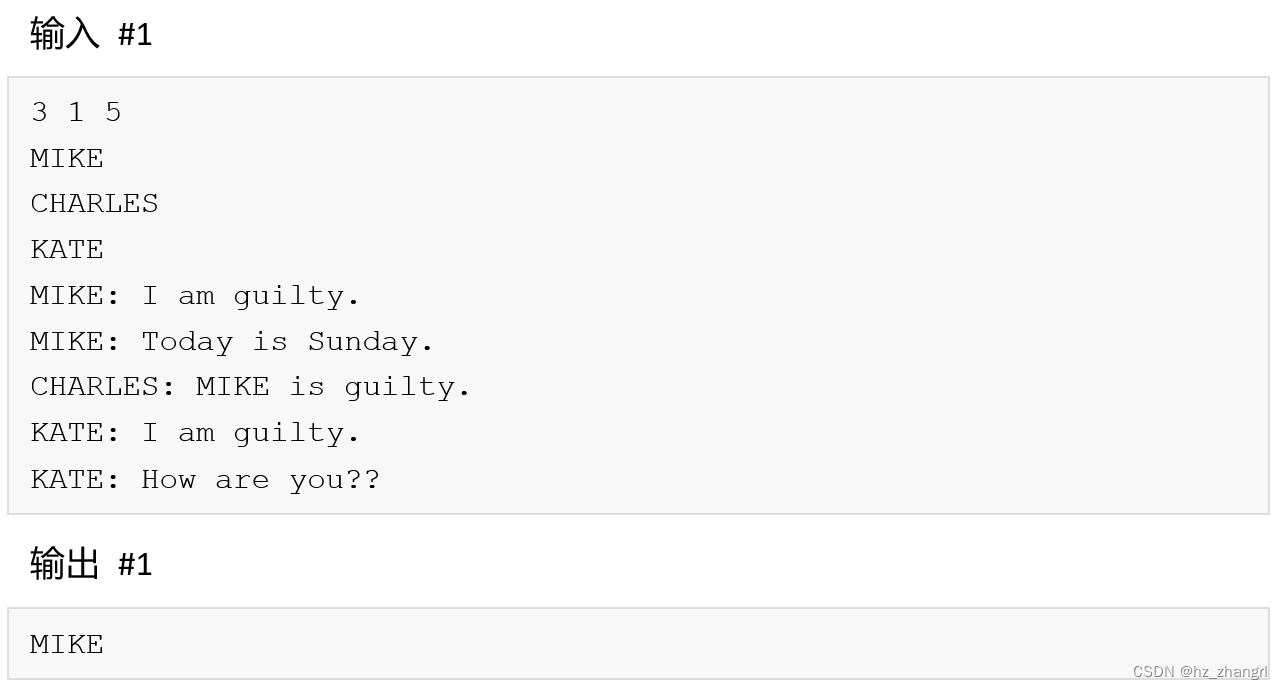
说明/提示

对于 100% 数据，满足1≤M≤20，0≤N≤M，1≤P≤100。

【题目来源】

NOIP 2003提高组第二题

解题思路：

单凭一条条证言判断某人是说真话还是假话是很难的，但因为只有一名罪犯，所以枚举每位同学，假设某同学是罪犯，来判断各条证言是否成立来判定某人是说真话还是假话？

另外证言中有说今天是星期几，但不能确定当天是星期几，无法直接判定是说真话还是假话？所以也要枚举星期，然后根据n个人是始终说谎的来判断说谎的同学。

每个句子有三种情况：真话、假话、废话。最终只要假话数量≤n≤假话数量 + 废话数量，那么说谎的同学就有可能有n个。

正确理解题目

只有以下五种句式的证言是有效证言，其余都是无效证言(废话)。

I am guilty.

I am not guilty.

XXX is guilty.

XXX is not guilty.

Today is XXX.

证词的含义

说真话、说假话与是否是罪犯没有任何关系。
XXX指认YYY是罪犯：若是真话，YYY就是罪犯；若是假话，YYY不是罪犯，罪犯是除YYY之外的某一个人。
XXX指认YYY不是罪犯：若是真话，YYY不是罪犯，罪犯是除YYY之外的某一个人；若是假话，YYY就是罪犯。
今天是星期几：用以辅助判断证人说的是真话还是假话。如两个人说的不是同个星期几，那么其中至少有人说假话。

注意题目中说“N个人始终说假话，其余的人始终说真”，意思是一个人的证词要么全部为真，要么全部为假。注意，不在上述类型的证词，可以算是真话，也可以算是假话。因为有“废话”存在，说真话人数不超过M-N，说假话人数不超过N。

推理算法

单从证词去推理是不可行的，因为不知道谁说了真话、谁说了假话，不能把真话、假话放在一起推理。

思路就是枚举某人是罪犯，再枚举今天是星期几，然后就可以判断每个证言是说真话还是假话。

每次枚举时，标记每个人说的是什么话，如果一个人既说真话又说假话，那就说明你的假设不成立，与题目矛盾，直接跳过此种情况。

如找不到罪犯则输出 Impossible；如果程序判断出罪犯超过1人，则输出Cannot Determine。

时间复杂度分析:

依次枚举可能的罪犯、星期几以及证言句子，所以总时间复杂度是O(7mp)，其中m是总人数，p是总证言数。

完整代码：

weekdays = ['Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday', 'Saturday', 'Sunday']

def parse(s):											# 解析证言句子，返回：“某人”说“某某人”是/不是罪犯，或今天是星期几
    name, test = s.split(': ', 1)
    if test == 'I am guilty':							# 某人说自己是罪犯
        return (name, name, 'yes')
    elif test == 'I am not guilty':						# 某人说自己不是罪犯
        return (name, name, 'no')
    elif test.endswith(' is guilty'):					# 检测是否以' is guilty'结尾
        obj = test.split(' ')[0]						# 某人说某某人是罪犯
        return (name, obj, 'yes')
    elif test.endswith(' is not guilty'):				# 检测是否以' is not guilty'结尾
        obj = test.split(' ')[0]						# 某人说某某人不是罪犯
        return (name, obj, 'no')
    elif test.startswith('Today is '):
        day = test.split(' is ')[1]						# 某人说今天是星期几
        return (name, None, 'day', day)
    else:												# 无效证言
        return (name, None, None)

def analyze(testimony, guilty, weekday):
    if testimony[2] == 'yes':
        return guilty == testimony[1]
    elif testimony[2] == 'no':
        return guilty != testimony[1]
    elif testimony[2] == 'day':
        return weekday == testimony[3]

m, n, p = [int(i) for i in input().split()]
names = [input() for i in range(m)]						# 嫌疑犯名单
testimonys = [parse(input()[:-1]) for i in range(p)]	# 证言，去除尾部句点(.)

suspects = set()										# 嫌疑犯(去重)
for guilty in names:									# 枚举罪犯是谁
    for weekday in weekdays:							# 枚举今天是星期几
        judge = {}
        impossbile = False
        for testimony in testimonys:					# 枚举各证言测试在这种情况下是否为真
            speaker = testimony[0]
            result = analyze(testimony, guilty, weekday)
            if speaker not in judge and result != None:
                judge[speaker] = result
            elif speaker in judge and result != None and result != judge[speaker]:
                judge[speaker] = 'reject'
                impossbile = True
                break
        if not impossbile and list(judge.values()).count(True) <= m-n and list(judge.values()).count(False) <= n:
            suspects.add(guilty)

if len(suspects) == 0:									# 无解
    print('Impossible')
elif len(suspects) > 1:									# 多解
    print('Cannot Determine')
else:
    print(list(suspects)[0])