优快云访问首达1W，记录一下

虽然1W不多，但很有意义，算自嗨一把

坚持学习，坚持分享

正文开始：

记得第一次发博文的时候，才几十的访问，但也兴奋了许久。。。于是那会就感叹要是访问能到1万，那感觉肯定很棒，嘀咕着要是到1W了就奖励自己个啥东西，再于是1W就成了玩优快云里的第一个小目标，1W的梗就此诞生。。。

访问量只是一个数字，当然以后会有10W,20W,100W…这数字它本身不重要，重要的是分享的过程，是不断再学习提高的过程，是自我驱动的一种方式。

这是第一次截图留念的时候：

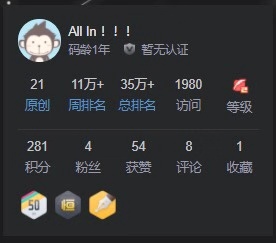
第二次：

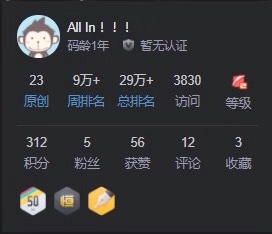
第三次：

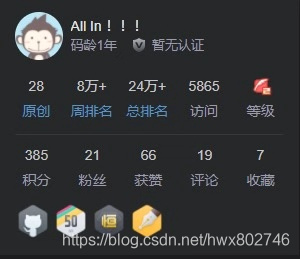
第四次：到了幸运数字6666~

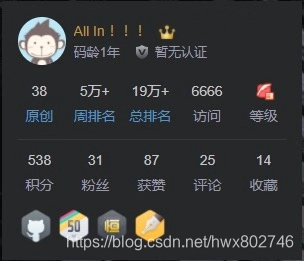
第五次： 7777~ 厂长：嗯？？？？？

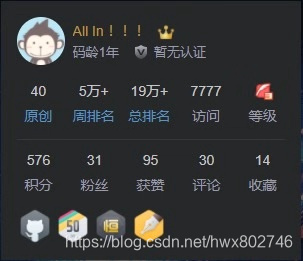
第六次：一觉醒来，" 小目标 "达成~~

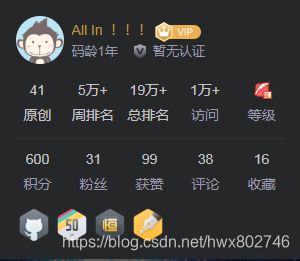
如今1万来了，多的不是兴奋，而是感叹分享的乐趣。在此建议还没参与到分享队伍中的同学，可以尝试发布自己的文章，在编辑的过程中，会加深自己对这个知识点的理解，理解是有模糊的理解的（这句比较绕），一旦将模糊的东西一个一个字写出来，就马虎不得，得需要特别清楚，这个时候就会想办法查漏补缺，那么这就是再学习的驱动。

小彩蛋：

还专门发Blink，我这“该死的”猴急心态…有心的同学可以点Blink进去看看

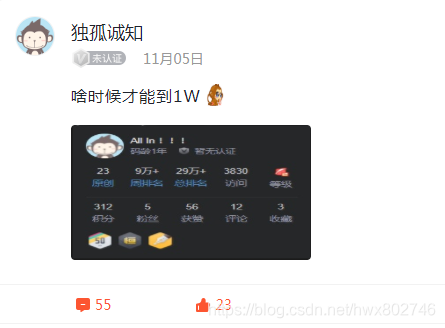
坚持学习，坚持分享，感谢诸位！

分享也是自己对问题再次加深理解的方式，可能不全面，但绝对有用，后面将不断完善~