关于logistic regression的思考

参考原文来自 http://www.cnblogs.com/549294286/p/3273296.html

http://www.hanlongfei.com/%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0/2015/08/05/mle/

1. logistic regression为什么能对线性问题进行预测？ 

我们都知道logistic regression可以用来处理线性问题，那么问题来了，logistic  regression为什么能对线性问题进行预测？

为了回答这个问题，首先要弄明白什么是线性预测。

1.1 什么是线性预测？

线性预测是通过线性模型来对样本进行的预测。线性模型是一个函数，这个函数通过属性的线性组合来对结果进行预测。线性模型分为经典线性模型 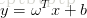  和广义线性模型 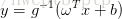。logistic regression用到的是广义线性预测。经典线性模型：自变量的线性预测结果就是因变量的估计值。广义线性模型：自变量的线性预测值的函数是因变量的估计值。常见的广义线性模型有：probit模型，poisson模型（泊松模型）、对数线性模型等。广义线性模型形式上是线性回归，但本质上上输入空间到输出空间的非线性函数映射。

1.2 二分类问题为什么没有使用传统的线性回归模型，而是是使用logistic regression？

线性回归用于而分类，首先想到的应该是 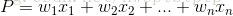 这个公式，这里，P对应分类的类别{0, 1}， 但是这个公式存在一些问题：

1）等式两边取值范围不同。等式右边的取值是整个实数集R，而左边取值是{0, 1}， 所以经典线性模型在分类问题中存在问题。（线性回归不能保证预测值的范围位于[0, 1]之间。）

2）实际问题中，很多情况下，当x很大或者很小时，对因变量P的影响很小，当x达到某个值时，对因变量P的影响很大。即在实际问题中，因变量P与自变量并不是直接的线性关系。所以，不能使用经典的线性模型，需要对经典线性模型进行休整，进而产生了广义线性模型。

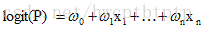
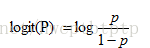（称为对数几率函数）

从而有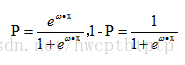

这里，P解决了上面的两个问题。

3. 如何求解logistic regression方程？

在logistic regression中，Y服从二项分布，误差服从二项分布而不是高斯分布，所以不能用最小二乘法进行模型参数估计，可以采用极大似然估计来进行参数估计。（ps：最小二乘法通常用于正态分布场合）

使用似然函数求目标函数

        严谨一点的公式如下：

        

        似然函数如下：

        

        对数似然函数，优化目标函数如下：

        

         整个逻辑回归问题就转化为求解目标函数，即对数似然函数的极大值的问题，即最优化问题，可采用梯度下降法、拟牛顿法。