《面试准备》c/c++全排列问题

问题描述

排列：从n个元素中任取m个元素，并按照一定的顺序进行排列，称为排列；

全排列：当n==m时，称为全排列；

比如：集合{ 1,2,3}的全排列为：

{ 1 2 3}

{ 1 3 2 }

{ 2 1 3 }

{ 2 3 1 }

{ 3 2 1 }

{ 3 1 2 }

算法思路：

(1)n个元素的全排列=（n-1个元素的全排列）+（另一个元素作为前缀）；

(2)出口：如果只有一个元素的全排列，则说明已经排完，则输出数组；

(3)不断将每个元素放作第一个元素，然后将这个元素作为前缀，并将其余元素继续全排列，等到出口，出口出去后还需要还原数组；

代码

#include <iostream>
#include <math.h>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <string.h>
using namespace std;
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
int sum = 0;
void swap(char str[],int a,int b){
	char tmp = str[a];
	str[a] = str[b];
	str[b] = tmp;
}

void perm(char ch[],int begin,int end){
	if(begin == end){
		for(int i=0;i<=end;i++){
			cout<<ch[i];
		}
		cout<<endl;
		sum++;
		return;
	}
	else{
		for(int j=begin;j<=end;j++){
			swap(ch,begin,j);
			perm(ch,begin+1,end);
			swap(ch,j,begin);

		}
	}
}

int main(int argc, char *argv[]) {
	int n = 0;
	char ch[100];
	gets(ch);
	for(int i=0;i<100;i++){
		if(ch[i]=='\0')
			break;
		n++;
	}
	perm(ch,0,n-1);	
	cout << sum;
    cout << endl;		
	return 0;
}

有重复元素的排列问题

思路：去重的全排列就是从第一个数字起每个数分别与它后面非重复出现的数字交换。

#include <iostream>
#include <math.h>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <string.h>
using namespace std;
/* run this program using the console pauser or add your own getch, system("pause") or input loop */
int sum = 0;
void swap(char str[],int a,int b){
	char tmp = str[a];
	str[a] = str[b];
	str[b] = tmp;
}

bool isswap(char str[],int begin,int end){
	for(int i=begin;i<end;i++){
		if(str[i]==str[end])
			return false;
	}
	return true;
}

void perm(char ch[],int begin,int end){
	if(begin == end){
		for(int i=0;i<=end;i++){
			cout<<ch[i];
		}
		cout<<endl;
		sum++;
		return;
	}
	else{
		for(int j=begin;j<=end;j++){
			if(isswap(ch,begin,j)){
				swap(ch,begin,j);
				perm(ch,begin+1,end);
				swap(ch,j,begin);
			}
		}
	}
}

int main(int argc, char *argv[]) {
	int n = 0;
	char ch[100];
	gets(ch);
	for(int i=0;i<100;i++){
		if(ch[i]=='\0')
			break;
		n++;
	}
	perm(ch,0,n-1);	
	cout << sum;
    cout << endl;		
	return 0;
}

测试：

输入：1232

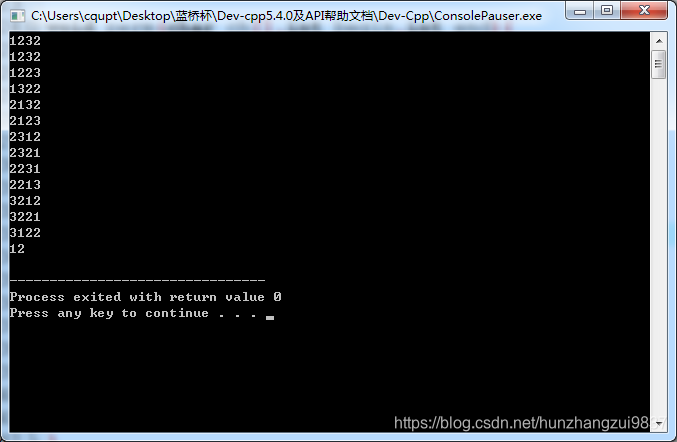
例子: 

寒假作业:

现在小学的数学题目也不是那么好玩的。
看看这个寒假作业：

   □ + □ = □
   □ - □ = □
   □ × □ = □
   □ ÷ □ = □
   
每个方块代表1~13中的某一个数字，但不能重复。
比如：
 6  + 7 = 13
 9  - 8 = 1
 3  * 4 = 12
 10 / 2 = 5

以及： 
 7  + 6 = 13
 9  - 8 = 1
 3  * 4 = 12
 10 / 2 = 5

就算两种解法。（加法，乘法交换律后算不同的方案）
 
你一共找到了多少种方案？

请填写表示方案数目的整数。
注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。
代码：

#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;

int res=0;
int a[]={1,2,3,4,5,6,7,8,9,10,11,12,13};
void dfs(int start)
{
	if(start>=3 )
	  if(a[0]+a[1]!=a[2]) return ;//对确定的前面三个数字进行等式判断，不符合，就不继续往下搜索
	if(start>=6)
	  if(a[3]-a[4]!=a[5]) return ;//同理进行第二个等式的判断，进行剪枝
	if(start>=9)
	  if(a[6]*a[7]!=a[8]) return ;
	if(start>=12)
	  if(a[11]*a[10]==a[9])
	  {
	  	for(int i=0;i<12;i++)
	  	  cout<<a[i]<<" ";
	  	cout<<endl;
		res++;
		return ;
	  }
	for(int i=start;i<=12;i++){
		int temp=a[start];
		a[start]=a[i];
		a[i]=temp;

		dfs(start+1);

		temp=a[start];
		a[start]=a[i];
		a[i]=temp;
	}
}
int main()
{
	dfs(0);
	cout<<res<<endl;
	return 0;
}