《面试准备》深度优先算法（dfs）介绍以及相关实例（c/c++）

DFS算法由来：

发明深度优先算法的是John E.Hopcroft 和 Robert E.Tarjan。1971~1972年，他们在斯坦福大学研究图的连通性（任意两点是否可以相互到达）和平面性（图中所有的边相互不交叉。在电路板上设计布线的时候，要求线与线不能交叉，这就是平面性的一个实际应用），发明了这个算法。他们也因此获得了1986年的图灵奖。

实例1：迷宫搜救

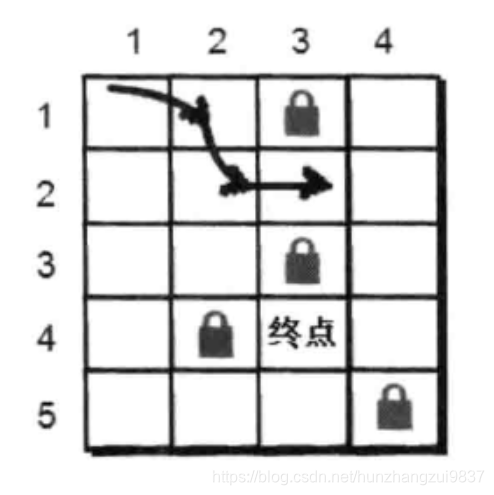
问题描述：A处于迷宫的入口处（1,1），B在（p,q）。找从（1,1）到（p,q）的最短路径（步长），如图：

输入描述：

整数n m:分别代表迷宫的行和列；

a[n][m]:用1表示有障碍，0表示无障碍；

start end p q:分别代表起始坐标和终点坐标；

输出描述：

整数step 最短步长

例如：

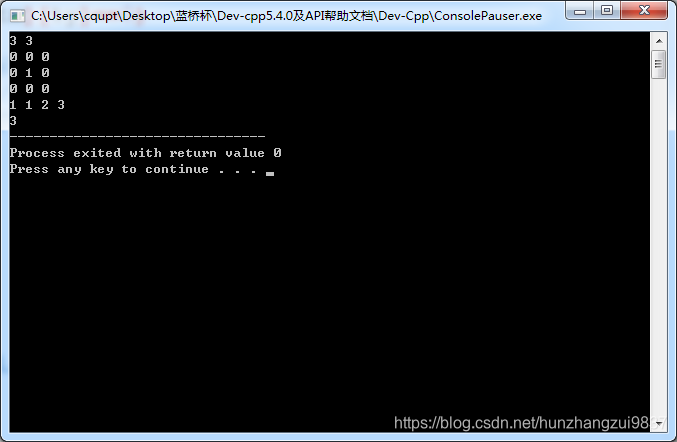
输入：

3 3

0 0 0

0 1 0

0 0 0

1 1 2 3

输出：

3

代码（c/c++）：

#include<stdio.h>
int n,m,p,q,min=99999999;
int a[51][51],book[51][51];
void dfs(int x,int y,int step)
{
    int next[4][2]={
    {0,1},//向右走
    {1,0},//向下走
    {0,-1},//向左走
    {-1,0},//向上走 
    };
    int tx,ty,k;
    if(x==p && y==q)  //判断是否到达小哈的位置 
    {
        if(step<min)
            min=step;  //更新最小值
        return; 
    }
    /*枚举四种走法*/ 
    for(k=0;k<=3;k++)
    {
        /*计算下一个点的坐标*/
        tx=x+next[k][0];
        ty=y+next[k][1];
        if(tx<1 || tx>n || ty<1 || ty>m)  //判断是否越界
            continue;
        /*判断该点是否为障碍物或者已经在路径中*/
        if(a[tx][ty]==0 && book[tx][ty]==0)
        {
            book[tx][ty]=1;  //标记这个点已经走过
            dfs(tx,ty,step+1);  //开始尝试下一个点
            book[tx][ty]=0;  //尝试结束，取消这个点的标记 
        } 
    }
    return;
} 

int main()
{
    int i,j,startx,starty;
    scanf("%d %d",&n,&m);  //读入n和m，n为行，m为列
    /*读入迷宫*/
    for(i=1;i<=n;i++)
        for(j=1;j<=m;j++)
            scanf("%d",&a[i][j]);
    scanf("%d %d %d %d",&startx,&starty,&p,&q);  //读入起点和终点坐标
    /*从起点开始搜索*/
    book[startx][starty]=1;  //标记起点已经在路径中，防止后面重复走
    dfs(startx,starty,0);  //第一个参数是起点的x坐标，以此类推是起点的y坐标，初始步数为0
    printf("%d",min);  //输出最短步数
    return 0; 
}

测试：

 实例2：单位分数（题目来自蓝桥杯）

题目描述：

可以把1分解为若干个互不相同的单位分数之和。

例如：
1 = 1/2 + 1/3 + 1/9 + 1/18
1 = 1/2 + 1/3 + 1/10 + 1/15
1 = 1/3 + 1/5 + 1/7 + 1/9 + 1/11 + 1/15 + 1/35 + 1/45 + 1/231
等等，类似这样的分解无穷无尽。
我们增加一个约束条件：最大的分母必须不超过30(说明：这个应该是包含30，但是下面举例的时候又没包含30)
请你求出分解为n项时的所有不同分解法。
数据格式要求：
 
例如，
输入：
4
程序应该输出：
1/2 1/3 1/8 1/24
1/2 1/3 1/9 1/18
1/2 1/3 1/10 1/15
1/2 1/4 1/5 1/20
1/2 1/4 1/6 1/12
再例如，
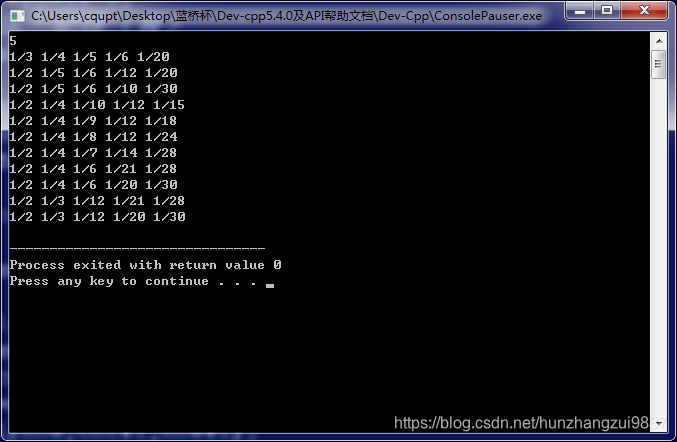
输入：
5
程序应该输出：
1/2 1/3 1/12 1/21 1/28
1/2 1/4 1/6 1/21 1/28
1/2 1/4 1/7 1/14 1/28
1/2 1/4 1/8 1/12 1/24
1/2 1/4 1/9 1/12 1/18
1/2 1/4 1/10 1/12 1/15
1/2 1/5 1/6 1/12 1/20
1/3 1/4 1/5 1/6 1/20

代码：

#include <iostream>
#include <cmath>
using namespace std;
 
int n,ans[15];
const double eps=1e-9;
//深度优先算法  记住（背） 
void dfs(double sum,int cnt,double now)
{
    if(cnt==n){
        if(abs(sum-1)<eps){
            for(int i=0;i<n;i++)
                cout<<1<<'/'<<ans[i]<<' ';
            cout<<endl;
        }
        return ;
    }
    if(sum>=1||cnt>n||now>30)
        return ;
    dfs(sum,cnt,now+1);
    ans[cnt]=now;
    dfs(sum+1/now,cnt+1,now+1);
    return ;
}
 
int main()
{
    cin>>n;
    dfs(0,0,1);
    return 0;
}

测试：

 实例3：方块分割（题目来自蓝桥杯） 

题目描述：

6x6的方格，沿着格子的边线剪开成两部分。

要求这两部分的形状完全相同。

如图：就是可行的分割法。

试计算：

包括这3种分法在内，一共有多少种不同的分割方法。

注意：旋转对称的属于同一种分割法。

请提交该整数，不要填写任何多余的内容或说明文字。

思路：

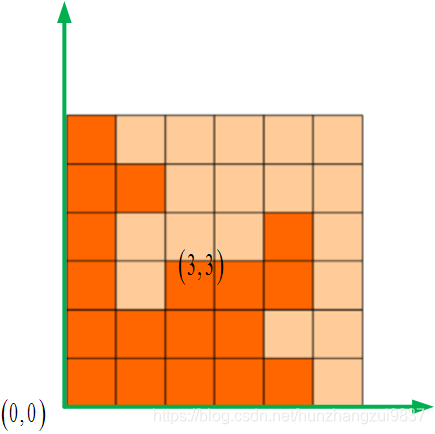
仔细思考，你会发现其实一道dfs的题目，建立坐标系，从坐标（3,3）移动，每移动一点，对称坐标锁住。

 代码：

#include<cstdio>
#include <cstdlib>
#include <iostream>
#include <queue>
#include <map>
#include <algorithm>
using namespace std;


bool book[23][23] = {};
int cnt = 0;
int nextx[4] = {-1, 0, 1, 0};
int nexty[4] = {0, -1, 0, 1};
void dfs(int stx, int sty)
{
    if(stx == 0 || stx == 6 || sty == 0 || sty == 6)
    {
        cnt++;
        return;
    }
    for(int i = 0; i < 4; i++)
    {
        int xx = stx + nextx[i];
        int yy = sty + nexty[i];
        if(!book[xx][yy])
        {
            book[xx][yy] = true;            //锁 
            book[6 - xx][6 - yy] = true;    //锁 
            dfs(xx, yy);
            book[xx][yy] = false;         //取消锁      
            book[6 - xx][6 - yy] = false; //取消锁  
        }
    }
}
int main()
{
    book[3][3] = true;
    dfs(3, 3);
    cout << cnt / 4 << endl;      //考虑旋转 
    return 0;

}

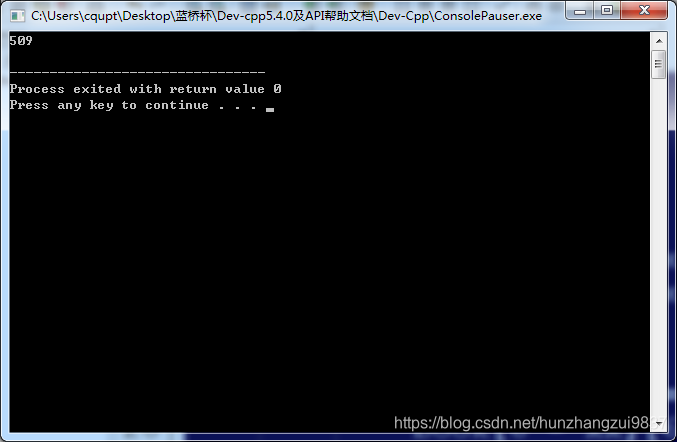
测试：