数据结构与算法之链表

这里是引用

如何分析、统计算法的执行效率和资源消耗？

多项式时间复杂度。

O(1)
首先你必须明确一个概念，O(1) 只是常量级时间复杂度的一种表示方法，并不是指只执行了一行代码。比如这段代码，即便有 3 行，它的时间复杂度也是 O(1），而不是 O(3)。

 int i = 8;
 int j = 6;
 int sum = i + j;

我稍微总结一下，只要代码的执行时间不随 n 的增大而增长，这样代码的时间复杂度我们都记作 O(1)。或者说，一般情况下，只要算法中不存在循环语句、递归语句，即使有成千上万行的代码，其时间复杂度也是Ο(1)。

O(logn)、O(nlogn)

 i=1;
 while (i <= n)  {
   i = i * 2;
 }

 i=1;
 while (i <= n)  {
   i = i * 3;
 }

实际上，不管是以 2 为底、以 3 为底，还是以 10 为底，我们可以把所有对数阶的时间复杂度都记为 O(logn)。为什么呢？我们知道，对数之间是可以互相转换的，log3n 就等于 log32 * log2n，所以 O(log3n) = O(C * log2n)，其中 C=log32 是一个常量。基于我们前面的一个理论：在采用大 O 标记复杂度的时候，可以忽略系数，即 O(Cf(n)) = O(f(n))。所以，O(log2n) 就等于 O(log3n)。因此，在对数阶时间复杂度的表示方法里，我们忽略对数的“底”，统一表示为 O(logn)。

O(m+n)、O(m*n)

int cal(int m, int n) {
  int sum_1 = 0;
  int i = 1;
  for (; i < m; ++i) {
    sum_1 = sum_1 + i;
  }

  int sum_2 = 0;
  int j = 1;
  for (; j < n; ++j) {
    sum_2 = sum_2 + j;
  }

  return sum_1 + sum_2;
}

从代码中可以看出，m 和 n 是表示两个数据规模。我们无法事先评估 m 和 n 谁的量级大，所以我们在表示复杂度的时候，就不能简单地利用加法法则，省略掉其中一个。所以，上面代码的时间复杂度就是 O(m+n)。针对这种情况，原来的加法法则就不正确了，我们需要将加法规则改为：T1(m) + T2(n) = O(f(m) + g(n))。但是乘法法则继续有效：T1(m)*T2(n) = O(f(m) * f(n))。

最好情况时间复杂度（best case time complexity）、最坏情况时间复杂度（worst case time complexity）、平均情况时间复杂度（average case time complexity）、均摊时间复杂度（amortized time complexity）

// n表示数组array的长度
int find(int[] array, int n, int x) {
  int i = 0;
  int pos = -1;
  for (; i < n; ++i) {
    if (array[i] == x) pos = i;
  }
  return pos;
}

你应该可以看出来，这段代码要实现的功能是，在一个无序的数组（array）中，
查找变量 x 出现的位置。如果没有找到，就返回 -1。按照上节课讲的分析方法，
这段代码的复杂度是 O(n)，其中，n 代表数组的长度。



// n表示数组array的长度
int find(int[] array, int n, int x) {
  int i = 0;
  int pos = -1;
  for (; i < n; ++i) {
    if (array[i] == x) {
       pos = i;
       break;
    }
  }
  return pos;
}
因为，要查找的变量 x 可能出现在数组的任意位置。如果数组中第一个元素正好是要查找的变量 x，
那就不需要继续遍历剩下的 n-1 个数据了，那时间复杂度就是 O(1)。但如果数组中不存在变量 x，
那我们就需要把整个数组都遍历一遍，时间复杂度就成了 O(n)。所以，不同的情况下，
这段代码的时间复杂度是不一样的。

数组：为什么很多编程语言中数组都从0开始编号？

如何实现随机访问？

什么是数组？我估计你心中已经有了答案。不过，我还是想用专业的话来给你做下解释。数组（Array）是一种线性表数据结构。它用一组连续的内存空间，来存储一组具有相同类型的数据。

第一是线性表（Linear List）。顾名思义，线性表就是数据排成像一条线一样的结构。每个线性表上的数据最多只有前和后两个方向。其实除了数组，链表、队列、栈等也是线性表结构。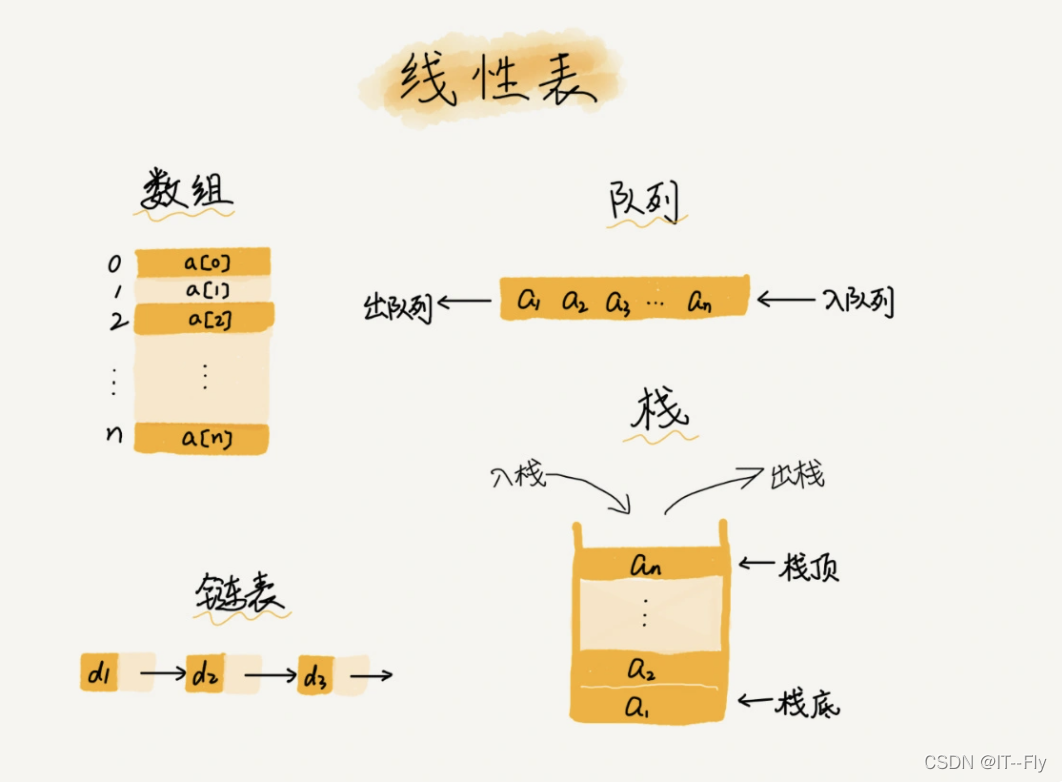
而与它相对立的概念是非线性表，比如二叉树、堆、图等。之所以叫非线性，是因为，在非线性表中，数据之间并不是简单的前后关系

容器能否完全替代数组？

1.Java ArrayList 无法存储基本类型，比如 int、long，需要封装为 Integer、Long 类，而 Autoboxing、Unboxing 则有一定的性能消耗，所以如果特别关注性能，或者希望使用基本类型，就可以选用数组。

2. 如果数据大小事先已知，并且对数据的操作非常简单，用不到 ArrayList 提供的大部分方法，也可以直接使用数组。
3. 还有一个是我个人的喜好，当要表示多维数组时，用数组往往会更加直观。比如 Object[][] array；而用容器的话则需要这样定义：ArrayList > array。

对于业务开发，直接使用容器就足够了，省时省力。毕竟损耗一丢丢性能，完全不会影响到系统整体的性能。但如果你是做一些非常底层的开发，比如开发网络框架，性能的优化需要做到极致，这个时候数组就会优于容器，成为首选

链表（上）：如何实现LRU缓存淘汰算法?

1. 如果此数据之前已经被缓存在链表中了，我们遍历得到这个数据对应的结点，并将其从原来的位置删除，然后再插入到链表的头部。
2. 如果此数据没有在缓存链表中，又可以分为两种情况：
   如果此时缓存未满，则将此结点直接插入到链表的头部；
   如果此时缓存已满，则链表尾结点删除，将新的数据结点插入链表的头部。

如何轻松写出正确的链表代码？这样我们就用链表实现了一个 LRU 缓存，是不是很简单？

技巧一：理解指针或引用的含义
将某个变量赋值给指针，实际上就是将这个变量的地址赋值给指针，或者反过来说，指针中存储了这个变量的内存地址，指向了这个变量，通过指针就能找到这个变量。

技巧二：警惕指针丢失和内存泄漏
插入结点时，一定要注意操作的顺序，要先将结点 x 的 next 指针指向结点 b，再把结点 a 的 next 指针指向结点 x，这样才不会丢失指针，导致内存泄漏。

同理，删除链表结点时，也一定要记得手动释放内存空间，否则，也会出现内存泄漏的问题。当然，对于像 Java 这种虚拟机自动管理内存的编程语言来说，就不需要考虑这么多了。

技巧三：利用哨兵简化实现难度

我们先来回顾一下单链表的插入和删除操作。如果我们在结点 p 后面插入一个新的结点，只需要下面两行代码就可以搞定。

new_node->next = p->next;
p->next = new_node;

但是，当我们要向一个空链表中插入第一个结点，刚刚的逻辑就不能用了。我们需要进行下面这样的特殊处理，其中 head 表示链表的头结点。所以，从这段代码，我们可以发现，对于单链表的插入操作，第一个结点和其他结点的插入逻辑是不一样的。

if (head == null) {
  head = new_node;
}

我们再来看单链表结点删除操作。如果要删除结点 p 的后继结点，我们只需要一行代码就可以搞定。

p->next = p->next->next;

但是，如果我们要删除链表中的最后一个结点，前面的删除代码就不 work 了。跟插入类似，我们也需要对于这种情况特殊处理。写成代码是这样子的：

if (head->next == null) {
   head = null;
}

技巧四：重点留意边界条件处理

如果链表为空时，代码是否能正常工作？
如果链表只包含一个结点时，代码是否能正常工作？
如果链表只包含两个结点时，代码是否能正常工作？
代码逻辑在处理头结点和尾结点的时候，是否能正常工作？

技巧五：举例画图，辅助思考

技巧六：多写多练，没有捷径

单链表反转

public class LinkedListCreator {

    /**
     * 这个递归，返回值只是为了控制返回的是最后一个节点
     * 然后通过递归通过栈的特性，这里就是让它可以从最后一个节点开始把自己的子节点的子节点改成自己
     * 自己的子节点改为null
     *
     * 递归的实现总是这么的简单，代码简练就是递归的好处，而且逻辑易于处理，只要能够出找出一层的逻辑，然后找出特殊值和出口，一个递归就已经完成啦
     *
     * 这里出口显然就是那个if，为的是找到最后一个节点，然后就可以开始往前递归反转，同时这个if可以排除参数只有一个节点，参数为null的情况。
     *
     * 递归的栈累计到最高层的时候（递归本质是栈，每一次递归放入一个栈，如果这层运行结束，就会弹出，运行下一层），最后一个if结束以后，
     * 开始反转， 反转的逻辑其实很简单， 吧当前节点的下一个节点指向自己，然后自己指向null

     * @param node
     * @return
     */
    public Node reverseLinkedList(Node node) {
        if (node.getNode() == null || node == null) {
            return node;
        }
        Node newData = reverseLinkedList(node.getNode());
        node.getNode().setNode(node);
        node.setNode(null);
        return newData;
    }

    public Node reverserLinkedList2(Node node){
        Stack<Node> nodeStack = new Stack<>();
        Node head = null;
        //存入栈中 模拟递归开始的栈状态
        while (node != null){
            nodeStack.push(node);
            node = node.getNode();
        }
        //特殊处理第一个栈顶元素（也就是反转前的最后一个元素，因为它位于最后，不需要反转，
        //如果它参与下面的while， 因为它的下一个节点为空，如果getNode()， 那么为空指针异常）
        if(!nodeStack.isEmpty()){
            head = nodeStack.pop();
        }
        while (!nodeStack.isEmpty()){
            Node tempNode = nodeStack.pop();
            tempNode.getNode().setNode(tempNode);
            tempNode.setNode(null);
        }
        return head;
    }

    public Node reverserLinkedList3(Node node){
        //指向空，可以想象成位于第一个节点之前
        Node newNode = null;
        // 指向第一个节点
        Node curNode = node;

        //循环中，使用第三变量事先保存curNode的后面一个节点
        while (curNode != null){
            Node tempNode = curNode.getNode();
            //把curNode 反向往前指
            curNode.setNode(newNode);
            //newNode向后移动
            newNode = curNode;
            //curNode 向后移动
            curNode = tempNode;
        }
        return newNode;
    }

}

链表中环的检测

两个有序的链表合并

删除链表倒数第 n 个结点

求链表的中间结点