230. 二叉搜索树中第K小的元素-优快云博客

本文链接：https://blog.youkuaiyun.com/lh686/article/details/125885592

该博客介绍了如何通过中序遍历优化寻找二叉搜索树中第k小元素的方法。首先，将二叉搜索树转换为升序排列的列表，然后返回第k个元素。为了优化，采用递归的中序遍历，一旦找到第k个元素，立即停止遍历，降低时间复杂度至O(h+k)，空间复杂度为O(h)。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

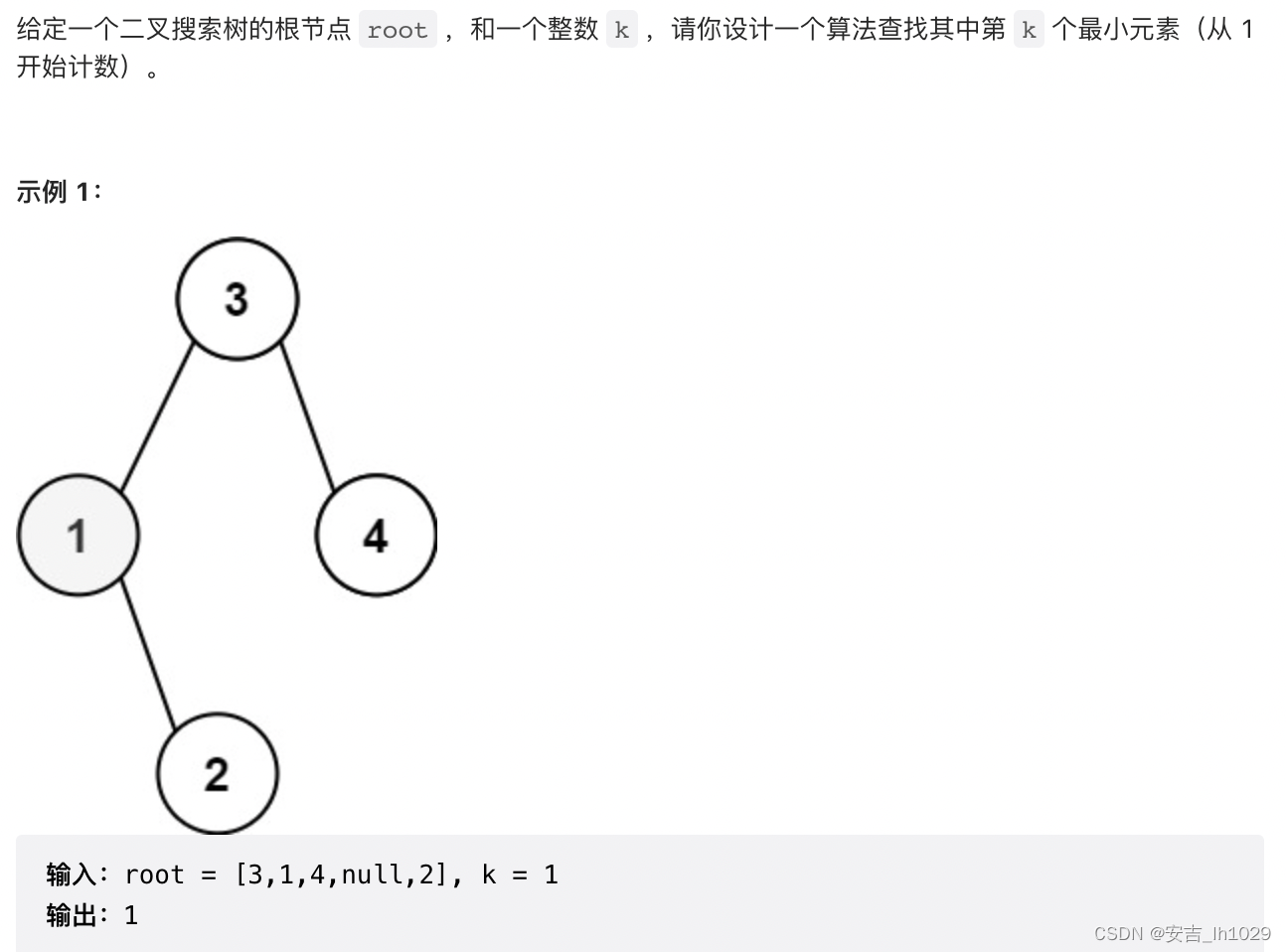
1、题目描述

2、题目分析

要寻找二叉搜索树中排序在第k个元素的位置，等价于需要把二叉搜索树进行【升序】排序。

即对应的转换为把二叉搜索树，转换为【中序】遍历，并存在容器中，可以是list, 数组，或者哈希表，队列均可以。

然后获取第k个位置，如本题我是使用list, index下标从0开始，因此第k个元素，即获取下标为k-1的元素即可，list.get(k-1); 代码如下：

class Solution {
    //二叉树进行中序遍历
     List<Integer> list = new ArrayList<Integer>();
    public int kthSmallest(TreeNode root, int k) {
       if(root == null) return -1;
       //此时list就是升序排列的
       dfs(root);
       if(list.size() >= k)
           return list.get(k-1);
       return -1;
    }

    private void dfs(TreeNode root){
         if(root == null) return;
         dfs(root.left);
         list.add(root.val);
         dfs(root.right);
    }

}

复杂度分析：

时间复杂度 O(N)：中序遍历，每个元素都遍历到，因此复杂度为 O(N)。
空间复杂度 O(N)：list中包含了全部元素，因此空间复杂度为O(N).

在上面基础上进行时间和空间复杂度度优化，即一旦获取到第k个元素，即停止。无需遍历全部到元素。

class Solution {
    int res;
    int sortK; // 排序后到第k个元素，这个需要是全局变量
    public int kthSmallest(TreeNode root, int k) {
       //【中序遍历】
       this.sortK = k;
       dfs(root);
       return res;
    }

    private void dfs(TreeNode root){
         if(root == null ||  sortK <= 0) return;
         dfs(root.left);
         if(--sortK == 0) res = root.val;
         dfs(root.right);
    }
}

复杂度分析：

时间复杂度：令 h 为树高，先到达叶子位置（最小节点位置），复杂度为 O(h)，然后找到第 k 小的元素，复杂度为 O(k)。整体 复杂度为 O(h+k)
空间复杂度：令 h 为树高，复杂度为 O(h)