打卡第十七天（问题：冒泡排序算法，扩展欧几里得算法）

1.冒泡排序

冒泡排序是主要排序算法的一种，思路简单明了，在数据基本有序的情况下，采用改进版，排序方法十分有效。

冒泡排序的基本思想是比较相邻两个元素，如果不是有序则进行交换，重复这个操作，直到全部数据有序为止。冒泡排序对待排序的数据（关键码）进行多趟处理，每一趟可以将一个大的数交换到右边适当的位置。

它的缺点是数据交换次数有可能比较多。

这里给出两个函数，一个是排序过程中，不考虑是否已经有序，按照固定的套路进行比较和交换，比较次数比较多；另外一个版本是如果已经有序，则停止处理，有额外的标志置值操作。

 

原始数据使用随机函数生成。

采用结构化程序设计，可以很容易改为从标准输入或文件读入数据，只需要修改函数getData即可。

数据个数由宏定义给出，也可以轻松地改为输入

• 冒泡排序算法程序：

• *

• * 一般的冒泡排序程序是函数bubblesort1。

• * 数据基本有序的情况下，应该使用改进版，即函数bubblesort2。

#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#define N 7
void getData(int [],int);
void outputData(int [],int);
void bubblesort1(int a[],int n);
void bubblesort2(int a[],int n);
int main(void)
{
    int a[N];
    getData(a,N);    //将数据放入数组a中；
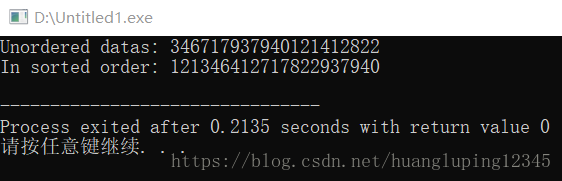
    printf("Unordered datas: ");
    outputData(a,N);
    bubblesort2(a,N);
    printf("In sorted order: ");
    outputData(a,N);
    return 0;
}
/*冒泡排序*/
void bubblesort1(int a[],int n)
{
    int i,j;
    for(i=n-1;i>0;i--)
    {
    for(j=1;j<=i;j++)
    if(a[j-1]>a[j]){
        int temp=a[j-1];//交换两个相邻的数
        a[j-1]=a[j];
        a[j]=temp;
    }
    }
}
/*冒泡排序改良版*/
void bubblesort2(int a[],int n)
{
    int i,j,swapflag=1;
    for(i=n-1;swapflag&&i>0;i--)
    {
        swapflag=0;
        for(j=1;j<=i;j++)
        if(a[j-1]>a[j]){
            int temp=a[j-1];
            a[j-1]=a[j];
            a[j]=temp;
            swapflag=1;
        }
    }
}
void getData(int d[],int n)
{
    time_t t;
    srand((unsigned) time(&t));//设置随机数起始值
    int i;
    for(i=0;i<n;i++)
    d[i]=rand()%1000;//获得0-999之间的整数值
}
void outputData(int d[],int n)
{
    int i;
    for(i=0;i<n;i++)
    printf("%d",d[i]);
    printf("\n");
}

结果：

2.扩展欧几里得算法

扩展欧几里得算法用于：
１．求不定方程
２．求解模的逆元

３．求解同余方程

• * 扩展欧几里得算法(extended Euclidean algorithm)

• * 扩展欧几里德算法是用来在已知a, b求解一组x，y，使它们满足贝祖等式：

• * ax+by = gcd(a, b) = d（解一定存在，根据数论中的相关定理）。

• * 扩展欧几里德常用在求解模线性方程及方程组中。

#include<stdio.h>
long exgcd1(long a,long b,long *x,long *y)//递归法
{
    if(b==0){
        *x=1;
        *y=0;
        return a;
    }
    long r=exgcd1(b,a%b,x,y);
    long t=*x;
    *x=*y;
    *y=t-a/b**y;
    return r;
 }
 long exgcd2(long a,long b,long *x,long *y)//递推法
 {
     long x0=1,y0=0,x1=0,y1=1;
     long r,q;
     *x=0;
     *y=1;
     r=a%b;
     q=(a-r)/b;
     while(r)
     {
         *x=x0-q*x1;
         *y=y0-q*y1;
         x0=x1;
         y0=y1;
         x1=*x;
         y1=*y;
         a=b;
         b=r;
         r=a%b;
         q=(a-r)/b;
     }
     return b;
 }
 int main(void)
 {
     long x,y;
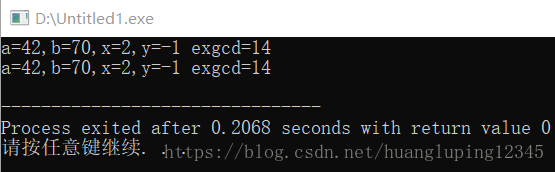
     printf("a=%d,b=%d,x=%ld,y=%ld exgcd=%ld\n",42,70,x,y,exgcd1(42,70,&x,&y));
     printf("a=%d,b=%d,x=%ld,y=%ld exgcd=%ld\n",42,70,x,y,exgcd2(42,70,&x,&y));
    return 0;
 }