咸鱼程序员之-Java算法第三篇-稀疏数组

1.定义：

稀疏数组可以看做是普通数组的压缩，但是这里说的普通数组是值无效数据量远大于有效数据量的数组

2.存储

为啥要压缩呢，

• 原数组中存在大量的无效数据，占据了大量的存储空间，真正有用的数据却少之又少

• 压缩存储可以节省存储空间以避免资源的不必要的浪费，在数据序列化到磁盘时，压缩存储可以提高IO效率

okay ，小编下面就开始举一个通俗的例子，你就明白了。。

 

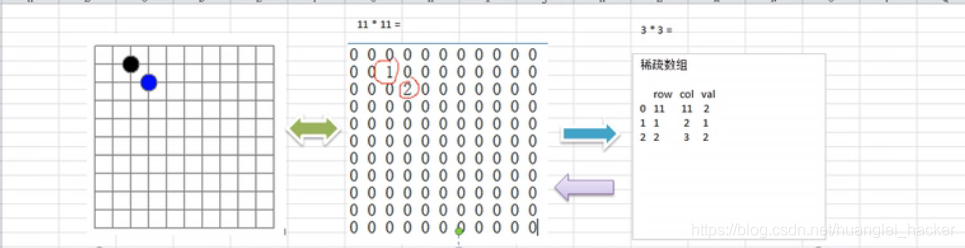
假设现在有11行11列的二维数组，其中除了二行三列和三行四列数据是有效的，其他都是0.。假设黑色的代表1，蓝色的代表2，，，

如果不压缩处理，这个数组就有11*11的大小，，，压缩过后就是3*3.。。可以看到空间大幅度减少的 。。。。

压缩的过程：

稀疏数组第一行第一列等于原始数组的行数

稀疏数组第一行第二列等于原始数组的列数

稀疏数组第一行第三列等于原始数组的有效数字的个数

稀疏数组第二行第一列等于原始数组第一个有效数字的行下标

稀疏数组第二行第二列等于原始数组第一个有效数字的列下标

稀疏数组第二行第三列等于原始数组第一个有效数字的值

同理。。稀疏数组的第三行则是存的第二个有效数字。。我们可以发现稀疏数组一定是三列。。。。

okay 下面我们就将二维数组和稀疏数组互转 。。。小编开始分析代码啦。。。。。。。。。。

------------------------------------------------这是一道华丽的分割线--------------------------------------------------------------

一般我们写算法之前，现弄清楚思路，这样写起来就会很轻松（这是小编自己的习惯)

思路：

 二维数组转稀疏数组的思路：

* 1.遍历原有的二维数组，得到有效数据的个数sum
* 2.根据sum 可以创建稀疏数组sparseArr int[sum+1][3]-稀疏数组一定是3列
 *3.将二维数组的有效数据存入稀疏数组

 稀疏数组转二维数组思路：
* 1.先读取稀疏数组第一行，根据第一行的第一列和第二列创建原来的二维数组
* 2.再读取稀疏数组后几行数据，并赋给原始的二维数组

 

二维数组转稀疏数组

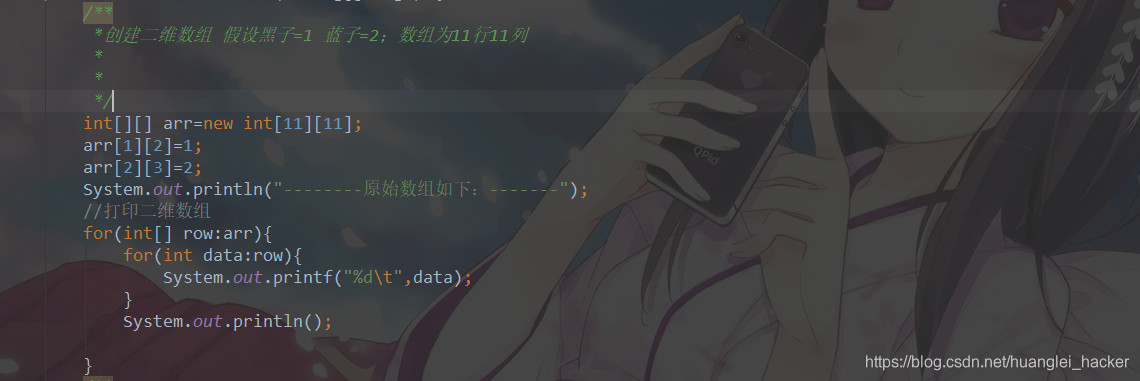
打印结果：

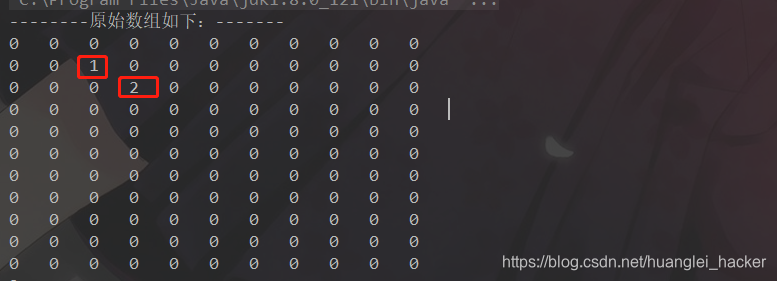
发现正确。。。

打印结果：

 

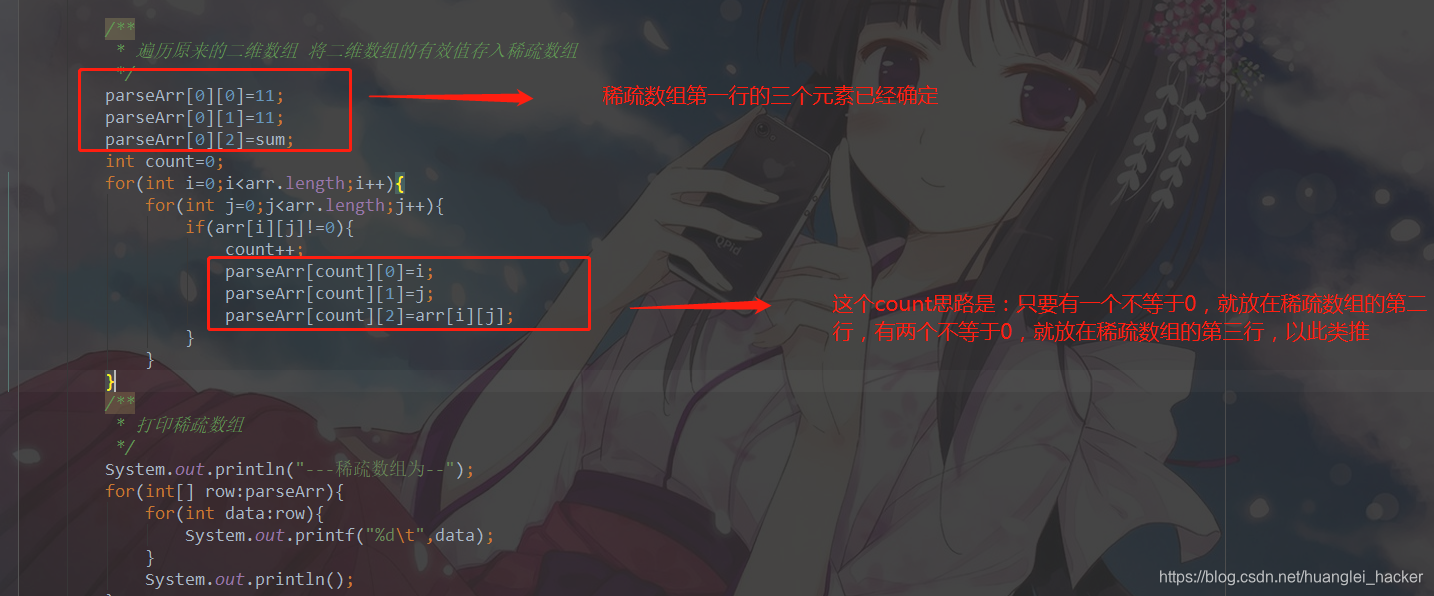
打印结果：

 

稀疏数组转二维数组：

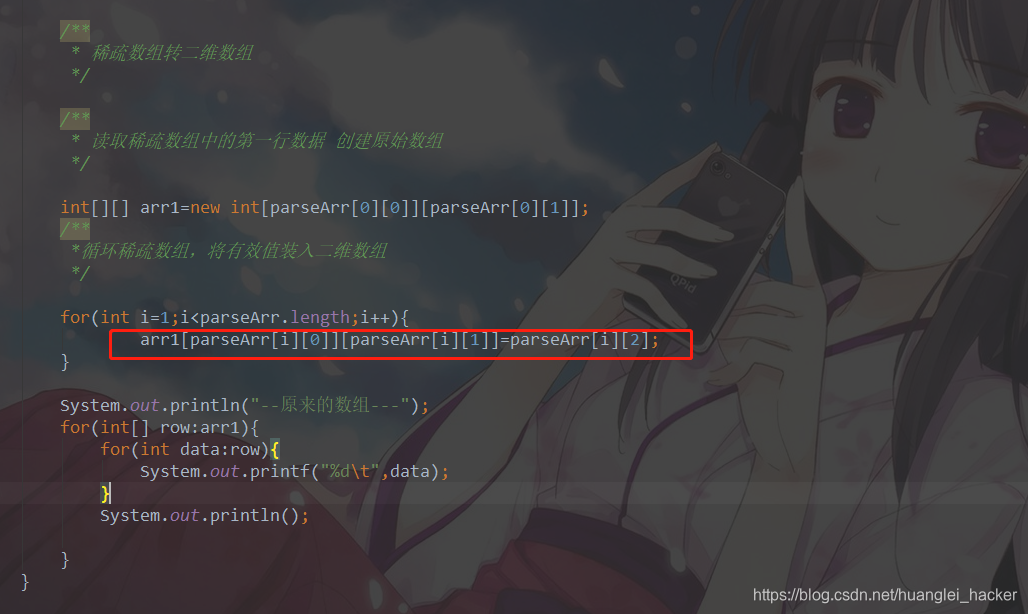
小编觉得难点在这一行，因为稀疏数组的列是固定的3列，所以只要一个for循环就能遍历完成。。。。。。

这里还需注意一点。。如下：

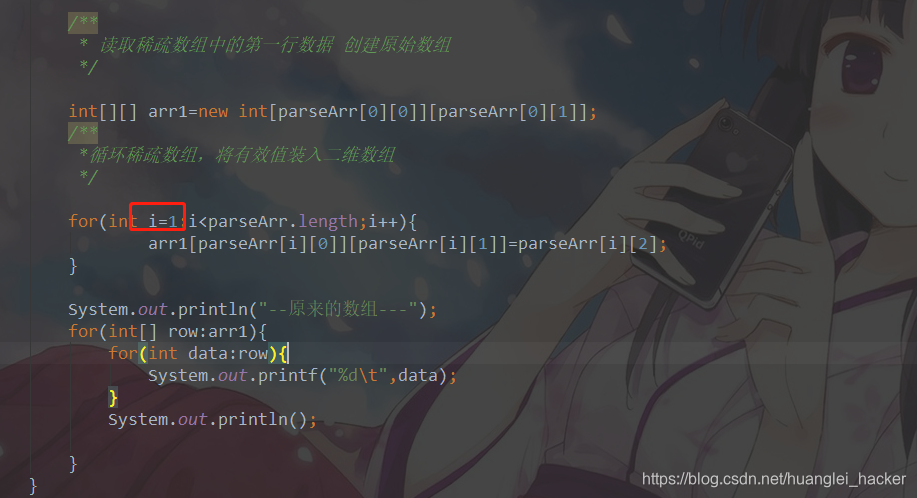
稀疏数组是从1(第二行)开始遍历的，因为第一行不是有效数据

 

okay ,关于稀疏数组。。小编就分析到这里啦，，希望可以对你有所帮助~~~~