OpenGL：Normal Mapping

最新推荐文章于 2025-12-08 18:21:57 发布

原创最新推荐文章于 2025-12-08 18:21:57 发布 · 1.1k 阅读

8 ·

CC 4.0 BY-SA版权

文章标签：

#OpenGL #图形渲染 #c++

什么是法线？

法线是垂直于物体表面（或顶点切面）的方向向量。运用法线，我们可以计算光照，从而能够达到更加真实的渲染效果。

几何定义

在平滑曲面上，某点的法线就是该点切平面的垂直方向
在三角网格中，每个顶点或每个面都有一个法线向量

什么是法线贴图？

法线贴图是一种 “存储表面法线信息” 的纹理贴图，用 RGB 颜色值编码法线方向，让低多边形（低模）模型呈现高多边形（高模）的凹凸细节。

原理

贴图的 RGB 通道对应法线的 X、Y、Z 轴方向（默认蓝色通道 Z 值占比高，所以法线贴图多呈蓝紫色）。
不需要增加模型面数，仅通过修改法线方向，就能模拟出划痕、褶皱、纹路等细节，大幅提升渲染效率。

法线贴图通常会呈现蓝紫色，因为法线贴图中的法线通常是从XY平面出发，指向+Z方向的。在贴图中的RGB分量分别对应法线的XYZ分量。这里需要注意的是在贴图中RGB的范围是 [0, 0.5]，而法线坐标的范围是 [-1, 1]，所以我们需要对法线坐标的范围进行转换：
$\begin{aligned} R = (X + 1) * 0.5 \\ G = (Y + 1) * 0.5 \\ B = (Z + 1) * 0.5 \end{aligned}$

什么是切线空间？

切线空间是建立在 3D 模型每个顶点上的 “局部坐标系”，由切线（T）、副切线（B）、法线（N）三个相互垂直的向量构成，专门用于存储法线贴图的法线信息。

T (Tangent)：切线方向，通常沿着UV坐标的U轴
B (Bitangent)：既垂直于法线N，也垂直于切线T。数学上是 N×T（叉乘），构成右手坐标系。它也应尽可能平行于纹理坐标V轴（T轴）增加的方向。网格纸“竖边”的3D方向。
N (Normal)：顶点法线，垂直于表面。它由模型原始顶点提供（可能已经过平滑处理或硬边处理）。它是垂直于该顶点处表面“宏观主平面”的方向（蓝色主轴）。

这三个向量是相互垂直的单位向量：|T| = |B| = |N| =1, T · B = 0, B · N = 0, N · T = 0。

在法线贴图中存储的法线向量 $n_{x},n_{y},n_{z})$ 就是该贴图点（顶点/片段）对应位置的切线空间中的法线。当我们用这个值作为当前的法线使用时，会出现一个问题，这个值是固定的，不会随着我们模型的变化而变化，这就会出现错误的光照计算，进而造成渲染出来的效果与我们预想出的不一样。

如下图所示，这个时候这面墙是立起来的，法线是朝向+Z方向（不一定是垂直），添加光照可以很好看到砖块之间的缝隙，这是我们想要渲染的效果。
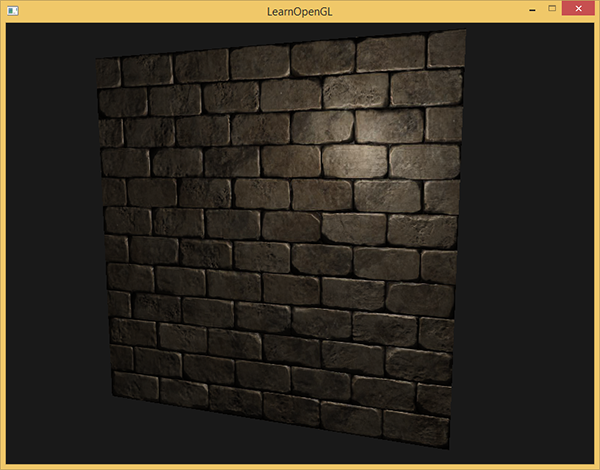
在这里插入图片描述
现在我们将这面墙“推倒”，再用光去照射它，可以看到光照是不正确的，很明显地可以看到圈出来的部分不应该这么暗，这是因为我们使用的法线贴图中的法线没有跟着我们的墙倒下而倒下。

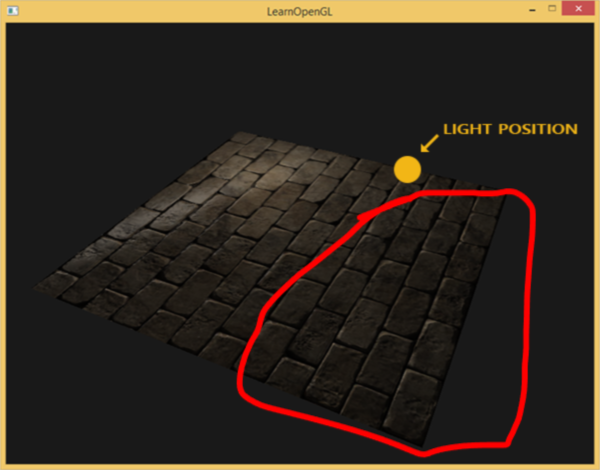
下面这张图中蓝色是法线向量，可以看到，它还是保持着原来的朝向，没有变化。
在这里插入图片描述

什么是TBN矩阵？

上面提到了法线贴图会出现的问题，我们使用TBN矩阵将 存储的‘切线空间法线’ (nₓ, nᵧ, n₂) 转换到一个公共坐标系（一般是世界空间） 中去，使得它可以和同样是世界空间的光线方向做点积运算。

$TBN=\begin{bmatrix} T_{x} & T_{y} & T_{z} \\ B_{x} & B_{y} & B_{z} \\ N_{x} & N_{y} & N_{z} \end{bmatrix}$
转换流程：

从法线贴图读取法线（在切线空间中）
用TBN矩阵将法线转换到世界空间
与世界空间的光照方向计算

如何得到TB向量？

TB向量来源于UV映射的几何关系：

切线(T) 指向UV坐标中U增加的方向
副切线(B) 指向UV坐标中V增加的方向

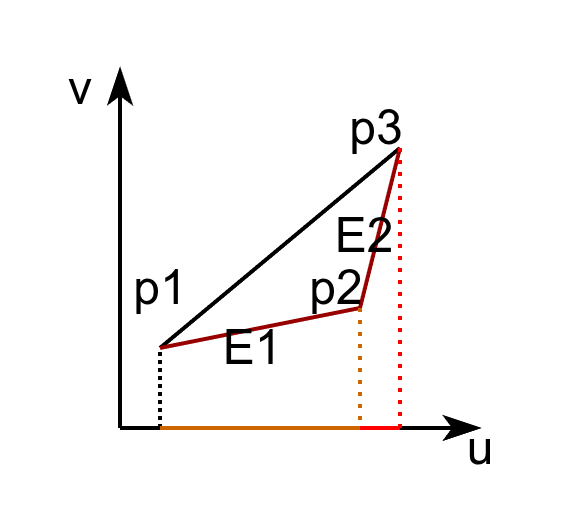
在这里插入图片描述

以上图为例，我们已知三角形的三个顶点的直接坐标和对应的uv坐标：

世界坐标：p1, p2, p3
UV坐标：(u1,v1), (u2,v2), (u3,v3)

我们可以列出边向量与UV变化之间的关系：
$\begin{aligned} E_{1} = p_{2} - p_{1} = \Delta u_{1} T + \Delta v_{1} B \\ E_{2} = p_{3} - p_{2} = \Delta u_{2} T + \Delta v_{2} B \end{aligned}$
其中 $Δu1=u2−u1,Δu2=u3−u2,Δv1=v2−v1,Δv2=v3−v2\Delta u_{1} = u_{2}-u_{1},\Delta u_{2}=u_{3}-u_{2},\Delta v_{1}=v_{2}-v_{1},\Delta v_{2}=v_{3}-v_{2}$ 。

将上面的式子进行展开：
$\begin{aligned} \begin{bmatrix} E_{1x} & E_{1y} & E_{1z} \\ E_{2x} & E_{2y} & E_{2z} \end{bmatrix} &= \begin{bmatrix} \Delta u_{1} & \Delta v_{1} \\ \Delta u_{2} & \Delta v_{2} \end{bmatrix} \begin{bmatrix} T_{x} & T_{y} & T_{z} \\ B_{x} & B_{y} & B_{z} \end{bmatrix} \\ \begin{bmatrix} \Delta u_{1} & \Delta v_{1} \\ \Delta u_{2} & \Delta v_{2} \end{bmatrix}^{-1} \begin{bmatrix} E_{1x} & E_{1y} & E_{1z} \\ E_{2x} & E_{2y} & E_{2z} \end{bmatrix} &= \begin{bmatrix} T_{x} & T_{y} & T_{z} \\ B_{x} & B_{y} & B_{z} \end{bmatrix} \\ \begin{bmatrix} T_{x} & T_{y} & T_{z} \\ B_{x} & B_{y} & B_{z} \end{bmatrix} &= \frac{1}{\Delta u_{1} \Delta v_{2} - \Delta v_{1}\Delta u_{2}} \begin{bmatrix} \Delta v_{2} & -\Delta v_{1} \\ -\Delta u_{2} & \Delta u_{1} \\ \end{bmatrix} \begin{bmatrix} E_{1x} & E_{1y} & E_{1z} \\ E_{2x} & E_{2y} & E_{2z} \end{bmatrix} \end{aligned}$

伪代码实现：

// 计算原始TB
for each triangle:
	E1 = p2 - p1;
	E2 = p3 - p2;
	double du1 = u2 - u1;
	double du2 = u3 - u2;
	double dv1 = v2 - v1;
	double dv2 = v3 - v2;
	
	double r = 1 / (du1 * dv2 - dv1 * du2);
	
	tangent = (dv2 * E1 - dv1 * E2) * r;
	bitanget = (du1 * E2 - du1 * E1) * r;
	
	// 累加到三个顶点
    vertex1.tangent += tangent
    vertex2.tangent += tangent
    vertex3.tangent += tangent
    
    vertex1.bitangent += bitangent
    vertex2.bitangent += bitangent
    vertex3.bitangent += bitangent

// 顶点级归一化
for each vertex:
	tangent = normalize(vertex.tangent);
	bitangetn = normalize(vertex.bitangent);
	
// 由于顶点法线N可能与T/B不垂直，必须重新正交化
T = normalize(T - dot(T, N) * N);
B = cross(N, T);