POJ 1459 && ZOJ 1734--Power Network【最大流dinic】

Power Network

Time Limit: 2000MS		Memory Limit: 32768K
Total Submissions: 25108		Accepted: 13077

Description

A power network consists of nodes (power stations, consumers and dispatchers) connected by power transport lines. A node u may be supplied with an amount s(u) >= 0 of power, may produce an amount 0 <= p(u) <= p_max(u) of power, may consume an amount 0 <= c(u) <= min(s(u),c_max(u)) of power, and may deliver an amount d(u)=s(u)+p(u)-c(u) of power. The following restrictions apply: c(u)=0 for any power station, p(u)=0 for any consumer, and p(u)=c(u)=0 for any dispatcher. There is at most one power transport line (u,v) from a node u to a node v in the net; it transports an amount 0 <= l(u,v) <= l_max(u,v) of power delivered by u to v. Let Con=Σ_uc(u) be the power consumed in the net. The problem is to compute the maximum value of Con. 

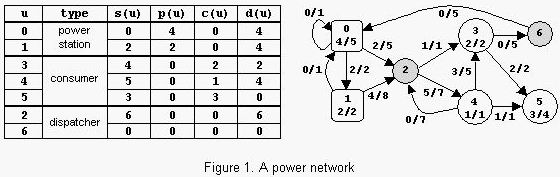
An example is in figure 1. The label x/y of power station u shows that p(u)=x and p_max(u)=y. The label x/y of consumer u shows that c(u)=x and c_max(u)=y. The label x/y of power transport line (u,v) shows that l(u,v)=x and l_max(u,v)=y. The power consumed is Con=6. Notice that there are other possible states of the network but the value of Con cannot exceed 6. 

Input

There are several data sets in the input. Each data set encodes a power network. It starts with four integers: 0 <= n <= 100 (nodes), 0 <= np <= n (power stations), 0 <= nc <= n (consumers), and 0 <= m <= n^2 (power transport lines). Follow m data triplets (u,v)z, where u and v are node identifiers (starting from 0) and 0 <= z <= 1000 is the value of l_max(u,v). Follow np doublets (u)z, where u is the identifier of a power station and 0 <= z <= 10000 is the value of p_max(u). The data set ends with nc doublets (u)z, where u is the identifier of a consumer and 0 <= z <= 10000 is the value of c_max(u). All input numbers are integers. Except the (u,v)z triplets and the (u)z doublets, which do not contain white spaces, white spaces can occur freely in input. Input data terminate with an end of file and are correct.

Output

For each data set from the input, the program prints on the standard output the maximum amount of power that can be consumed in the corresponding network. Each result has an integral value and is printed from the beginning of a separate line.

Sample Input

2 1 1 2 (0,1)20 (1,0)10 (0)15 (1)20
7 2 3 13 (0,0)1 (0,1)2 (0,2)5 (1,0)1 (1,2)8 (2,3)1 (2,4)7
         (3,5)2 (3,6)5 (4,2)7 (4,3)5 (4,5)1 (6,0)5
         (0)5 (1)2 (3)2 (4)1 (5)4

Sample Output

15
6

Hint

The sample input contains two data sets. The first data set encodes a network with 2 nodes, power station 0 with pmax(0)=15 and consumer 1 with cmax(1)=20, and 2 power transport lines with lmax(0,1)=20 and lmax(1,0)=10. The maximum value of Con is 15. The second data set encodes the network from figure 1.

题目给出很多都是废话，特别是符号s(u)，d(u)，Con还有那条公式都别管，混淆视听

难点在于构图

电站p(u)均为源点，用户c(u)均为汇点，中转站当普通点处理

结点和边都有 x/y（流量和容量），这个很容易使人产生矛盾（因为学习最大流问题是，只有 边 才有流量和容量。但是不难发现，题目所给的例图中有多个源点，多个汇点，多个普通点，只有源点和汇点才标有 x/y，普通点没有标x/y，而且所给出的所有边都有x/y。 这无疑在促使我们对图做一个变形： 建议一个超级源 s，一个超级汇 t，使 s 指向所有源点，并把源点的 容量y 分别作为这些边的 容量，使所有汇点指向 t，并把汇点的容量y分别作为这些边的 容量，然后本来是源点和汇点的点，全部变为普通点。这样就把“多源多汇最大流”变形为“单源单汇最大流”问题。

学习最大流问题时，会发现边上的流量值是给定初始值的，但是这题的输入只有容量，没有流量，很多人马上感觉到无从入手。其实边上的流量初始值为多少都没有所谓，解最大流需要用到的只有容量。但是一般为了方便起见， 会把所有边的流量初始化为0。这样做有一个最大的好处，就是可以回避 反向弧 的存在，

以上解析来自http://www.cnblogs.com/lyy289065406/archive/2011/07/30/2122116.html

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <iostream>
#include <queue>
#define maxn 300
#define maxm 100000
#define INF 0x3f3f3f3f
using namespace std;

int head[maxn], cur[maxn], cnt;
int dist[maxn], vis[maxn];
int n, np, nc, m;

struct node{
    int u, v, cap, flow, next;
};

node edge[maxm];

void init(){
    cnt = 0;
    memset(head, -1, sizeof(head));
}

void add(int u, int v, int w){
    edge[cnt] = {u, v, w, 0, head[u]};
    head[u] = cnt++;
    edge[cnt] = {v, u, 0, 0, head[v]};
    head[v] = cnt++;
}

void getmap(){
    int u, v, w;
    while(m--){
        scanf(" (%d,%d)%d", &u, &v, &w);//注意有空格
        add(u, v, w);
    }
    while(np--){
        scanf(" (%d)%d", &u, &w);
        add(n, u, w);// n 为源点, 源点和电站连接
    }
    while(nc--){
        scanf(" (%d)%d", &u, &w);
        add(u, n + 1, w); // n + 1 为汇点 ，消费者和汇点连接
    }
}

bool BFS(int st ,int ed){
    queue<int>q;
    memset(vis, 0 ,sizeof(vis));
    memset(dist, -1, sizeof(dist));
    vis[st] = 1;
    dist[st] = 0;
    q.push(st);
    while(!q.empty()){
        int u = q.front();
        q.pop();
        for(int i = head[u]; i != -1; i = edge[i].next){
            node E = edge[i];
            if(!vis[E.v] && E.cap > E.flow){
                vis[E.v] = 1;
                dist[E.v] = dist[u] + 1;
                if(E.v == ed)
                    return true;
                q.push(E.v);
            }
        }
    }
    return false;
}

int DFS(int x, int ed, int a){
    if(x == ed || a == 0)
        return a;
    int flow = 0, f;
    for(int &i = cur[x]; i != -1; i = edge[i].next){
        node &E = edge[i];
        if(dist[E.v] == dist[x] + 1 && (f = DFS(E.v, ed, min(a, E.cap - E.flow))) > 0){
            E.flow += f;
            edge[i ^ 1].flow -= f;
            a -= f;
            flow += f;
            if(a == 0)
                break;
        }
    }
    return flow;
}

int maxflow(int st, int ed){
    int flowsum = 0;
    while(BFS(st,ed)){
        memcpy(cur, head, sizeof(head));
        flowsum += DFS(st, ed, INF);
    }
    return flowsum;
}

int main (){
    while(scanf("%d%d%d%d", &n, &np, &nc, &m) != EOF){
        init();
        getmap();
        printf("%d\n", maxflow(n, n + 1));
    }
    return 0;
}