Deep Residual Learning for Image Recognition

Deep Residual Learning for Image Recognition

Abstract

深度神经网络不利于训练。本文提出一个残差网络模型以便训练更深的网络模型。本文通过丰富的实验证明残差网络更容易优化，同时在更深的网络中获得更高的精确度。使用ImageNet 数据集进行评估，残差网络达到152层，比VGG网络深8倍。同时产生较好的结果。

Introduction

特征可随着网络的不断加深进行堆叠。增加网络深度极大提高网络对特征的提取。
但随着网络的加深，也带来的梯度爆炸的问题。[23, 9, 37, 13]使用规范初始化，[16]使用中间归一化层解决网络加深中的梯度爆炸问题。
当网络不断加深并开始收敛时，精度也开始达到饱和后然后开始下降。精度的下降不是由过度拟合引起的，而是在适当的深度模型中添加更多的层会导致更高的训练误差。如下图所示：

训练精度的下降表明并非所有的系统都同样容易优化。我们考虑一个浅层网络和一个相对应的结构的深度网络（向浅层网络中加入一些层）。通过构建一个更深层次网络模型解决这个问题：添加层次是标识的映射，其他层次从浅层网络复制过来。通过这种解的构造证明，更深的模型不应产生比较浅的模型更高的训练误差。但是实验结果显示，更深的模型并没有产生更好的结果。
本论文通过设计一个残差网络解决该问题。与以往的网络模型不同，我们让网络适应残差映射。一般的，定义底层网络向上层映射为$H(x)$，我们需要非线性层适应另一个映射关系$F(x):=H(x)-x$，将原始映射重塑为$F(x)+x$。我们假设与原映射相比，残差映射更容易优化。另一方面，如果原映射是最优的，那么残差映射会将残差项将为0。
残差网络可以通过快捷连接实现，如下图：

快捷连接不会产生额外的参数以及复杂计算，整个网络仍可以使用SGD进行训练，可通过公开库实现。
本文在ImageNet数据集上进行精度消失问题以及评估网络模型的适应。我们需要展示：（1）深度残差网络更容易优化，随着网络深度的增加，相比相当层次深度得普通网络训练错误率更低；（2）随着网络深度的增加，与先前的网络相比，我们的深度残差网络获得更好的精度。
通过在多个数据集上实验证明，残差学习网络原理是通用的，未来可使用于其他视觉和非视觉问题。

Related Work

Residual Representations：略
Shortcut Connections：相对比其他论文，在本论文中的快捷连接是无参数的，当关闭快捷连接时，网络模型将变为非残差模型。相反，我们的网络构想是学习残差函数，网络中的快捷连接从未关闭，所有的上下文信息总在网络中传递使得残差网络不断的学习。

Deep Residual Learning

Residual Learning

$H(x)$为一个底层输入，等价于假设它们可以渐进逼近残差函数，$H(x)-x$(假设输入、输出相同维度、尺寸)。我们不使用这些层去拟合$H(x)$，使用这些层拟合$F(x):=H(x)-x$。原函数为$F(x)+x$。虽然这两种形式可作为拟合函数，但学习的难易程度是不同。

Identity Mapping by Shortcuts

采用残差模型去拟合几个堆叠层。如下图所示：

由上图所得$y=f(x,W_i)+x$，其中x，y为输入、输出向量。$f(x,W_i)$表示要学习的残差映射。如上图所示，有两层，$F=W_2\sigma (W_{1}x)$，其中$\sigma$为ReLu，为了简化符号，偏差省略。$F+x$为快捷连接和像素级别加分。
本文中快捷连接没有引入额外参数以及复杂计算，这在比较评估原始网络和残差网络是十分重要的。我们在参数数量、深度、宽度以及计算复杂度。
$y=f(x,W_i)+x$公式中x和F的尺寸必须相同。若x和F的尺寸不同，在快捷连接之前对x进行线性变换，公式如下：
$$y=F(x,W_i)+W_{s}x$$
在尺寸相同的情况下我们可使用方阵$W_s$，但是经过实验发现标识矩阵（个人连接此处为x）是解决精度退化比较有效和节省计算的方法，所以在尺寸不同时使用$W_s$即可。
残差函数F的组成是十分灵活的，实验中的残差函数有二或三层，如下图所示。

残差网络也适用于卷积层操作，$F(x,W_i)$可表示多个卷积层。残差的实现为通道级逐像素相加。

Network Architectures

我们测试多个普通/残差网络，并发现其中一致的特性。为了方便讨论，利用ImageNet数据集设计两种网络模型。
Plain Network（普通网络）：34-layer plain

Residual Network（残差网络）：34-layer residual

Implementation

使用ImageNet数据集，调整图片尺寸，其较短的边在[256,480]进行随机采样。在图片中随机裁剪出224 X 224图像块，并进行水平翻转；使用批归一化；初始化权重，批量大小为256，使用SGD进行优化。
测试中，为了进行比较，采用了 10-crop进行测试。
【这里所谓的 10-crop 是指在 test 的时候，从原始图片及翻转后的图片中，从四个 corner 和 一个 center 各 crop 一个 (224, 224) 的图片，总共 10 张，然后对这10张图片进行 classification，对10次预测的结果 average。】
为了得到更好的结果，我们采用了全卷积网络，并评价多尺度图片的分类结果。图片的尺度在 {224, 256, 384, 480, 640}中选取。

Experiments

ImageNet Classification

我们在ImageNet 2012 分类数据集评价网络，该数据集包括1000个类。我们评估指标包括top-1和top-5的错误率。
Plain Networks对于普通网络，我们评价了18层和34层。网络结构如下：

下表显示了34层网络比18层的验证误差更大。

整个训练过程中34层网络具有更高的训练错误率，即使18层网络的解空间是34层网络 的子空间。
我们认为梯度消失不是造成优化困难的原因。所有的普通网络都是用了批量归一化，这确保了正向传播信号具有非零方差，我们同时也验证了反向传播在BN下的梯度状况。所以正向和反向传播的信号都没有出现消失。事实上，普通34层网络已经能够达到分类的准确度，如表3所示。我们猜测较深的普通网络可能发生以指数较低的收敛速度，从而影响训练错误率降低。由于此原因，优化困难在未来仍旧是一个重点。

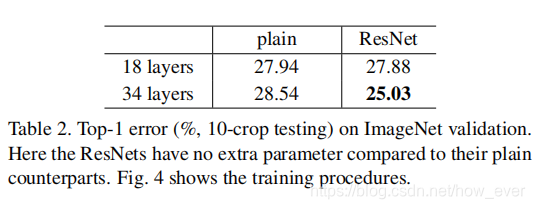
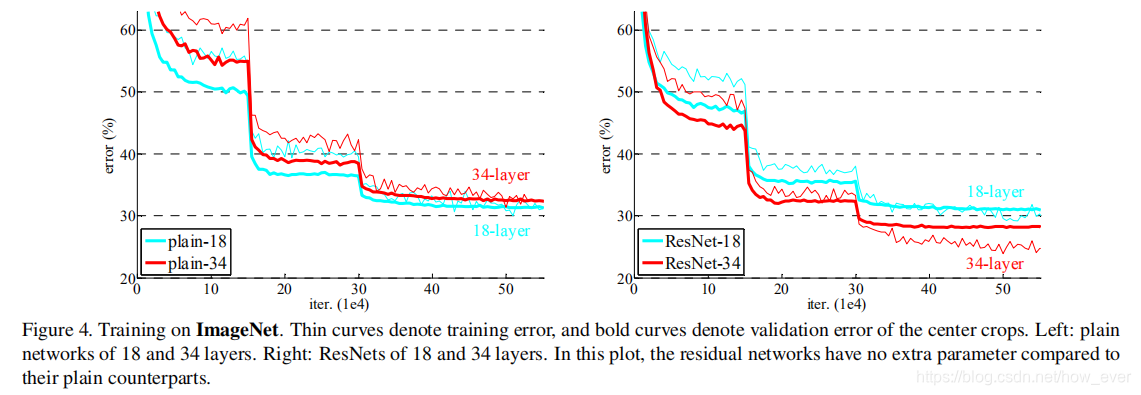
Residual Networks. 接下来评估18层和34层的残差网络，从表二和图四（右）可发现：（1）在同一分类任务下34层残差网络的效果比18层残差网络好。34层残差网络具有更低的训练误差，并且可推广到验证集中。这表明，精度退化问题通过残差网络很好的解决了，我们从深度增加的网络中获得了更高的准确度。（2）与普通的网络相比，34层残差网络top-1错误率下降了3.5%（表二），训练错误率也有明显下降（图4 右vs.左）。这种比较验证了剩余学习在极深网络上的有效性。
最后对18层的残差网络和18层的普通网络进行比较评估，由表二和图四显示18层残差网络的结果优于普通网络。同时在此种情况下，通过增加残差项使得优化速度更快。